Im dritten Schuljahr lernen die Kinder mit der schriftlichen Addition das erste Mal ein algorithmisches Verfahren zur Lösungsbestimmung kennen. In Abgrenzung zum Kopfrechnen und dem halbschriftlichen Rechnen, die dem Zahlenrechnen zugeordnet werden, müssen die Kinder eine andere Art zu rechnen entwickeln - denn bei den schriftlichen Verfahren wird mit Ziffern gerechnet. Um diese Verfahren verständig auszuführen, geht es deshalb wie bei den halbschriftlichen Strategien nicht nur darum, die Algorithmen schnell auszuführen, sondern die Kinder sollen Sicherheit und Flexibilität auf einer verständnisbasierten Grundlage erlangen.
Durch eine genauere Betrachtung von Fehlern lassen sich häufig Rückschlüsse darauf ziehen, an welchen Stellen dieser Algorithmus noch nicht vollständig verstanden wurde. Entsprechend haben sich die Studentinnen Beyoglu & Kötterheinrich (2010) sowie Tenbergen & Transchel (2010) im Rahmen ihrer Bachelorarbeiten genauer mit den Schwierigkeiten von Kindern bei der schriftlichen Addition auseinandergesetzt und insbesondere das Verständnis der Kinder zum Übertrag genauer in den Blick genommen.
Auf dieser Seite werden die wesentlichen Erkenntnisse der Arbeiten vorgestellt und anhand von Schülerdokumenten illustriert. Sie bekommen einen Überblick über mögliche Fehlvorstellungen, die Bedeutung des Übertrags und haben die Chance Ihre Diagnosefähigkeiten zu testen.
Sophia rechnet schriftlich 876+145
Eigenaktivität
Wie könnte Sophia zu dem Ergebnis gekommen sein? Was vermuten Sie?
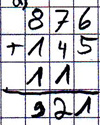
Hier finden Sie eine kompetenzorientierte Analyse von Sophias Rechnung.
Hintergrundwissen zur schriftlichen Addition
Die schriftliche Addition ist für viele Kinder das unkomplizierteste der vier schriftlichen Rechenverfahren (vgl. Padberg & Benz 2011, S. 229). Zugleich ist es der erste komplexe Algorithmus, mit dem die Kinder in Kontakt treten. Trotz des niedrigen Schwierigkeitgrades müssen die Kinder einige Voraussetzungen mitbringen, um den Algorithmus zu erlernen. Hierzu zählen das Beherrschen des kleinen Einmaleins, ein tieferes Verständnis des Bündelungsprinzips sowie eine ausgeprägte Vorstellung der Größenordnung von Zahlen und Kompetenzen im Überschlagsrechnen (vgl. Padberg & Benz 2011, S. 232 f.). Grundlegend für den Erwerb sind demnach tragfähige Zahl- und Operationsvorstellungen (vgl MSW NRW 2008, S. 58).
Wichtig sind besonders das Verständnis vom Bündelungsprinzip und Stellenschreibweise (vgl. Radatz u. a. 1999, S. 120), da die schriftliche Addition an den Vorkenntnissen der Schüler im Bereich der halbschriftlichen Addition anknüpft (vgl. Fuchs u.a. 2005, S. 139). Hinzu kommt, dass die Kinder ein neues Zahlverständnis aufbauen müssen, da es sich beim schriftlichen Verfahren um ein reines Ziffernrechnen handelt (vgl. Gerster 2005, S. 232).
Heute liegt der Fokus daher nicht mehr darauf, dass die Kinder das Verfahren "im Schlaf" ausführen können (vgl. Schipper 2009, S. 180). Es ist wichtiger, dass sie das Verfahren verstehen, Zusammenhänge zwischen Aufgaben entdecken und so in der Lage sind, das Verfahren sinnvoll einzusetzen. So wird im Lehrplan auch gefordert, dass die Schüler das Verfahren in eigenen Worten erläutern können (vgl. MSW NRW 2008, S. 62).
Eine Strategie, um den verständnisvollen Erwerb der schriftlichen Rechenverfahren zu sichern, ist es, gezielt mit den Kindern die halbschriftliche Additionsstrategie (z. B. "Stellenwerte Extra") mit dem schriftlichen Algorithmus zu vergleichen. Sodass "der Zusammenhang zwischen beiden Wegen gut sichtbar" (Padberg & Benz 2011, S. 225) wird.
Verständnis des Algorithmus der schriftlichen Addition
Eine Möglichkeit, um das Verständnis des schriftlichen Additionsalgorithmus zu überprüfen, ist, die Kinder die Funktionsweise der schriftlichen Addition in eigenen Worten beschreiben zu lassen. So kann ein Eindruck gewonnen werden, inwieweit die Kinder den Algorithmus verstanden haben und diesen verbalisieren können.
Den Schülern wird hierzu beispielsweise folgende Rechenaufgabe eines anderen Kindes vorgelegt und sie gebeten, anhand dieser Rechnung zu erklären, wie das Kind vorgeht.
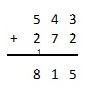
Erkläre, wie Tim gerechnet hat.
Die Aufgabe wurde durch 134 von 137 Kindern bearbeitet. Die entstandenen Beschreibungen können in folgende drei Kategorien eingeteilt werden.
1. Ausführliche Erklärung (44%)
Jeder Schritt des Algorithmus wird anhand der konkreten Zahlenwerte erläutert. Der Übertrag wird erwähnt und ggf. erklärt.

Katharina (3. Klasse)
Katharina beschreibt die einzelnen Rechenschritte des Algorithmus ausführlich anhand der konkreten Zahlenwerte. Des Weiteren erwähnt sie den Übertrag und erklärt, wie dieser aufzuschreiben ist.
2. Allgemeine Beschreibung (31%)
Es werden die Rechenschritte anhand der Benennung der Stellenwerte dargestellt.

Burak (4. Klasse)
Burak beschreibt die Rechenschritte des Algorithmus mit Hilfe der allgemeinen Benennung der Stellenwerte. Auf den Übertrag geht er jedoch nicht ein.
3. Unvollständige Beschreibung (25%)
Der Algorithmus des schriftlichen Rechenverfahrens wird nicht erläutert.

Stefan (4. Klasse)
Stefan geht nicht auf die einzelnen Rechenschritte des Verfahrens ein, sondern bezieht sich nur auf die beiden Zahlen, die addiert werden.
Typische Fehler und Schwierigkeiten
Wenn die Kinder den schriftlichen Algorithmus nur mechanisch ausführen, ihn aber nicht verstehen, können verschiedene Schwierigkeiten auftreten. Obwohl die Fehlerquote durchschnittlich nur etwa 5% beträgt (vgl. Gerster 1982, S. 28), gibt es einige typische Fehler, die beim schriftlichen Addieren entstehen können. Häufig werden diese als Flüchtigkeitsfehler akzeptiert, obwohl sie genauer thematisert werden müssten (vgl. Gerster 1982, S. 14), damit sich die Fehler bei den Kindern nicht festigen.
Um dem entgegenzuwirken und die Fehler bewusst richtigzustellen, ist es notwendig, dass die Lehrperson mit Hilfe informativer Aufgaben und im Rahmen von Standortbestimmungen das individuelle Verständnis der Kinder ermittelt. Hierzu gehört, dass sie die Schülerdokumente nachvollzieht und erkannte Schwierigkeiten im Unterricht thematisiert sowie gezielte Fördermaßnahmen ergreift.
Für die Konzeption einer Standortbestimmung zur schriftlichen Addition ist es von großer Bedeutung, Aufgaben zu wählen, die spezielle Fehler und Schwierigkeiten sichtbar machen, d.h. sie geradezu provozieren. Im Folgenden finden Sie zwei mögliche Standortbestimmungen und können sich in einer Eigenaktivität mit der Konzeption möglicher Aufgaben auseinandersetzen.
Standortbestimmung von Tenbergen und Transchel (2010)
Standortbestimmung von Beyoglu und Kötterheinrich (2010)
Eigenaktivität
Betrachten Sie die einzelnen Aufgaben aus der Standortbestimmung. Mit welchen Schwierigkeiten werden die Kinder jeweils konfrontiert?
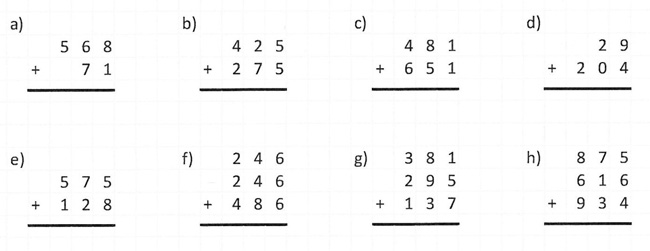
Eine Analyse der eingebauten Schwierigkeiten in den abgebildeten Aufgaben finden Sie hier.
Im Folgenden werden Sie einige Schülerdokumente sehen, anhand denen sich typische Fehler der schriftlichen Addition nachvollziehen lassen (in Anlehnung an Gerster 1982; Padberg & Benz 2011, S. 230 f.).
1. Fehlertyp
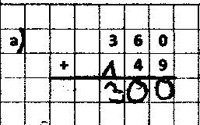
Beispiel: 360 + 49

Die Berechnung wird von links nach rechts durchgeführt. Die Überträge werden dabei in die falsche Stellenwertspalte übertragen.
2. Fehlertyp
Beispiel: 587 + 34
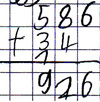
Falsches Stellenwertverständnis: Die Summanden der Aufgabe werden nicht stellengerecht untereinander notiert.
3. Fehlertyp
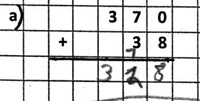
Beispiel: 77 + 985
Falsches Stellenwertverständnis: An der Einerstelle wird eine Ziffer hinzugefügt.
4. Fehlertyp
Beispiel: 583 + 228

Anstelle der Addition wird die Subtraktion angewendet.
5. Fehlertyp
Beispiel: 381 + 295 + 137
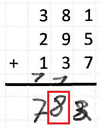
Perseverationsfehler: Einzelne Elemente spielen für die Kinder eine besondere Rolle. Beispielsweise wird eine Ziffer der Summanden bei der Notation des Teilergebnisses eingefügt.
6. Fehlertyp
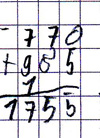
Beispiel: 370 + 38
Der Übertrag wird an der falschen Stelle notiert.
7. Fehlertyp
Beispiel 908 + 406
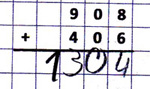
Es wird kein Übertrag zur Null notiert.
8. Fehlertyp
Beispiel: 481 + 315
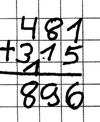
Es wird ein Übertrag zu viel notiert.
9. Fehlertyp
Beispiel: 876 + 145
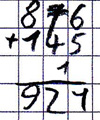
Es wird ein Übertrag vergessen.
10. Fehlertyp
Beispiel: 805 + 309
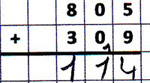
An der Leerstelle/ zusätzlichen Stelle wird kein Übertrag notiert.
11. Fehlertyp
Beispiel: 360 + 49

Es bestehen Probleme beim Rechnen mit der Null (0 + x = 0).
12. Fehlertyp
Beispiel: 586 + 34
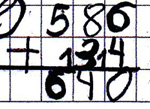
Es besteht ein Rechenfehler beim kleinen Einspluseins.
13. Fehlertyp
Beispiel 67 + 988
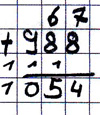
Es wird sich um 1 verrechnet (vermutlich durch falsches Weiterzählen).
14. Fehlertyp
Beispiel: 381 + 295 + 137
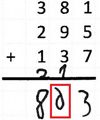
Der Übertrag wird allgemein nicht berücksichtigt.
15. Fehlertyp
Beispiel: 481 + 651
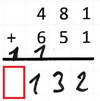
Der Übertrag wird in besonderen Fällen nicht berücksichtigt wie der Übertrag zur 9, einer leeren Stelle oder zum neuen Stellenwert.
16. Fehlertyp
Beispiel: 129 + 204
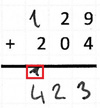
Es wird falsch mit der Übertragsziffer operiert wie bei der Notation an der falschen Stelle.
17. Fehlertyp
Beispiel: 29 + 204
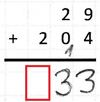
Es wird keine Ziffer an der leeren Stelle eines Summanden notiert.
Ihre Diagnosefähigkeit können Sie hier an einigen Schülerlösungen überprüfen.
Informationen zur Fehlerhäufigkeit finden Sie in den Ergebnissen der Bachelorarbeit von Beyoglu und Kötterheinrich (2010) und den Ergebnissen von Tenbergen und Transchel (2010).
Der Übertrag
Nach Gerster (1982) sind etwa die Hälfte der Schülerfehler Übertragsfehler. Für das verständnisbasierte Anwenden des Verfahrens ist es daher wichtig, das die Kinder wissen, wann ein Übertrag entsteht und welche Bedeutung die kleine Übertragseins hat.
Im Folgenden sehen Sie einige schriftliche Erklärungen von Schülern einer dritten Klasse zur Aufgabenstellung "Erkläre, warum man manchmal eine 1 übertragen muss.". Für die Kinder bietet diese Aufgabenstellung eine hohe Kompetenzanforderung, die je nach Leistungsstärke der Schüler unterschiedlich ausfallen kann. Bei genauer Betrachtung können aber auch in nicht eindeutigen Antworten, richtige Ansätze erkannt werden.
Eigenaktivität
- Versuchen Sie mit eigenen Worten zu erklären, warum man manchmal eine Eins übertragen muss. Schauen Sie sich die Schülerdokumente an und vergleichen Sie ihre Lösung mit denen der Schüler.
- Bei welchen Dokumenten würden Sie vermuten, dass das Kind verstanden hat, warum es manchmal eine Eins übertragen muss? Begründen Sie Ihre Vermutung.
- Wie würden Sie die Übertragseins im Unterricht thematisieren, nachdem Sie durch eine Standortbestimmung festgestellt haben, dass vermutlich noch nicht alle Kinder die Bedeutung der Übertragseins verstanden haben?

Michelle

Mareike

Jan
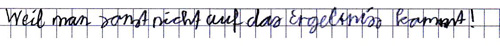
Lukas
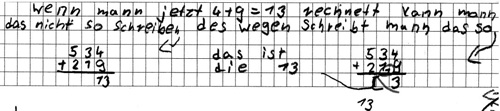
Lareen

Stefan

Timo
Im Kontext einer Standortbestimmung wurden Kinder gebeten, zu erklären, was die kleine Eins bedeutet. Von 137 Schülern haben 124 die Aufgabe bearbeitet. Die Schülerantworten lassen sich in folgende vier Kategorien einteilen.
1. Korrekt begründet (33%)
Ziffernvorstellung (80%)

Svenja (4. Klasse)
Svenja erklärt den Übertrag mit der Zehner-Überschreitung im vorhergehenden Stellenwert. Bei ihr dominiert die Ziffernvorstellung der Ergebnisse innerhalb eines Stellenwerts.
Zahlvorstellung (20%)
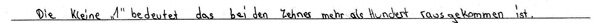
Katja (3. Klasse)
Katja erklärt den Übertrag mit der Überschreitung des Hunderters in der Zehnerspalte. Bei ihr dominiert die Vorstellung der Ergebnisse als ganze Zahl.
2. Beschreibend (27%)
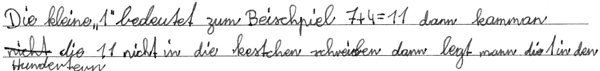
Sven (3. Klasse)
Sven nennt nicht ausdrücklich die Zehner-Überschreitung als Ursache für den Übertrag, sondern beschreibt, was man mit einer zweistelligen Zahl im Ergebnis machen muss.
3. Bezug zum Stellenwert (13%)
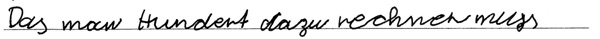
Philipp (3. Klasse)
Philipp deutet den Übertrag nur in Bezug zum Stellenwert und stellt keine Verbindung zum vorhergehenden Rechenschritt her, aus dem der Übertrag resultiert.
4. Kein Bezug zur Bedeutung des Übertrags (27%)
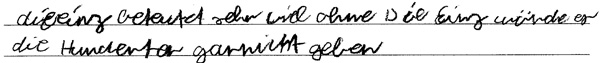
Sebastian (3. Klasse)
Sebastian geht nicht auf die Bedeutung oder Ursache des Übertrags ein.
Testen Sie Ihr Wissen zu dem Thema in unserem Kira-Check.
Verwandte Themen
Schriftliche Subtraktion
Schriftliche Multiplikation
Schriftliche Division
Halbschriftliche Addition
Informative Aufgaben
Im Pikas: Fortbildungsmodul: 'Lernen auf eigenen Wegen' finden Sie weitere Informationen zum Übergang vom Halbschriftlichen zum schriftlichen Rechnen sowie zum Rechnen auf eigenen Wegen.
Auf primakom: Materialeinsatz - Unterricht erfahren Sie, wie das Dienes-Material (Mehrsystemblöcke) zur Veranschaulichung der schriftlichen Rechenverfahren eingesetzt werden kann.
Material
Standortbestimmung von Tenbergen & Transchel (2010)Standortbestimmung von Beyoglu & Kötterheinrich (2010)
