Um Kinder in ihrem Lernen zu unterstützen, ist es nötig, sich in ihre individuellen Denkwege hineinzuversetzen. Dies gilt besonders, wenn die Kinder ganz andere Vorstellungen von bestimmten mathematischen Sachverhalten haben als Erwachsene und diese Vorstellungen zu Fehlern führen.
Wie solche Fehlvorstellungen aussehen können und dass hinter ihnen oftmals richtige Ideen stecken, zeigen wir auf dieser Seite am Beispiel der schriftlichen Multiplikation. Hier können Sie Ihr Wissen über typische Fehler bei der schriftlichen Multiplikation vertiefen und an ausgewählten Schülerdokumenten Ihre Diagnosefähigkeiten unter Beweis stellen.
643 ∙ 52 = 33706 ?
Eigenaktivität
- Lösen Sie die Aufgabe 643∙52 mithilfe des Verfahrens der schriftlichen Multiplikation.
- Vergleichen Sie Ihre Lösung mit der von Marleen. Wie ist Marleen zum Ergebnis 33706 gekommen?
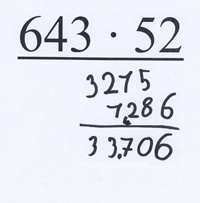
Marleens Lösung
Mithilfe des Videos können Sie Ihre Vermutung überprüfen:
Marleen
Hintergrundwissen: Das Verfahren der schriftlichen Multiplikation
Genau wie bei den schriftlichen Rechenverfahren der weiteren Grundrechenarten, steckt hinter der schriftlichen Multiplikation ein nicht unkomplizierter Algorithmus. Anders als beispielsweise bei der schriftlichen Addition, lässt sich das Verfahren der schriftlichen Multiplikation jedoch nicht direkt aus den halbschriftlichen Strategien der Multiplikation ableiten (vgl. Höhtker & Selter 1998, S.17).
Deshalb ist gerade bei der schriftlichen Multiplikation besondere Sorgfalt bei der Einführung des Verfahrens von Nöten, damit die Kinder das Verfahren nicht nur automatisiert anwenden, sondern den Schritt vom mündlichen und halbschriftlichen Zahlenrechnen zum schriftlichen Ziffernrechnen nachvollziehen können.
Dazu ist es im Sinne der fortschreitenden Schematisierung von Vorteil, auf die Vorkenntnisse der Schülerinnen und Schüler bzgl. der halbschriftlichen Multiplikation einzugehen. So schlagen Wittmann und Müller beispielsweise vor, an die halbschriftliche Strategie „Malkreuz" anzuknüpfen, von der es gut möglich ist, über die mittelalterliche Methode der Neperschen Streifen („Malstreifen") eine Beziehung zum schriftlichen Verfahren herzustellen (vgl. Wittmann & Müller 2005, S. 7 und S. 102 ff.; Höhtker & Selter 1998).
Die Bildungsstandards verlangen dass die schriftlichen Rechenverfahren, d.h. auch die schriftliche Multiplikation, nicht nur ausgeführt, sondern auch von den Kindern verstanden werden sollen (vgl. KMK 2005, S. 9).
Der Lehrplan NRW (vgl. MSW NRW 2008) präzisiert diese Forderung und verlangt als verbindliche Kompetenzerwartung den verständnisvollen Umgang mit den schriftlichen Rechenverfahren. So sollen die Schülerinnen und Schüler die schriftliche Multiplikation (auch mit mehrstelligen Faktoren) erläutern können, „[...] indem sie die einzelnen Rechenschritte an Beispielen in nachvollziehbarer Weise beschreiben" (MSW NRW 2008, S. 62).
Neben dem Verständnis bzw. der Einsicht in das Ziffernrechenverfahren, ist das sichere Ausführen der schriftlichen Multiplikation ein weiteres Ziel des Unterrichts (ebd.).
Um die im nächsten Abschnitt dargestellten Fehler und Schwierigkeiten bei der schriftlichen Multiplikation besser nachvollziehen zu können, wird nachfolgend das Verfahren der schriftlichen Multiplikation dargestellt. Padberg (2005) führt dazu die folgenden Charakteristika an:
- Beide Faktoren stehen in einer Zeile nebeneinander.
- Die rechte Zahl ist der Multiplikator, die linke der Multiplikand [...].
- Man beginnt die Multiplikation mit der höchsten Stelle des zweiten Faktors.
- Die Teilprodukte ordnet man jeweils ihrem Stellenwert entsprechend unter dem zweiten Faktor an und lässt die zugehörigen Endnullen fort (letzteres sollte nicht zu rasch erfolgen).
Padberg 2005, S. 269
Entstehen während der Berechnung eines Teilprodukts bei einer der Teilrechnungen zweistellige Ergebnisse, so wird ein Übertrag erforderlich. Dieser Übertrag kann in die Aufgabe geschrieben (siehe Beispiel unten), im Kopf bzw. mit Hilfe der Finger behalten oder auf dem Blatt notiert werden.
Im Folgenden wird das oben beschriebene Verfahren mit der üblichen Sprechweise am Beispiel des Dokuments von Viertklässler Hannes veranschaulicht.
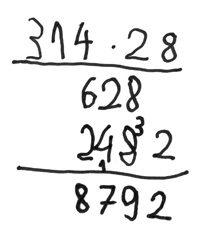
Sprechweise:
| 2 ∙ 4 = 8 |
Schreibe 8 |
| 2 ∙ 1 = 2 |
Schreibe 2 |
| 2 ∙ 3 = 6 |
Schreibe 6 |
| 8 ∙ 4 = 32 |
Schreibe 2, Übertrag 3 |
| 8 ∙ 1 = 8 |
Schreibe 8 |
| 8 ∙ 3 = 24 |
Schreibe 24 |
| 0 + 2 = 2 |
Schreibe 2 |
| 8 + 3 + 8 = 19 |
Schreibe 9, Übertrag 1 |
| 2 + 4 + 1 = 7 |
Schreibe 7 |
| 6 + 2 = 8 |
Schreibe 8 |
Typische Fehler und Schwierigkeiten bei der schriftlichen Multiplikation
Wie in Abschnitt 2 erläutert, ist der Algorithmus der schriftlichen Multiplikation für Kinder nicht per se mit Verständnis verbunden. Trotz sorgfältiger Einführung können Teilschritte des Verfahrens (z.B. der Übertrag) für die Kinder unverstanden bleiben, was zu viel Eigenkreativität im Vorgehen der Kinder führen kann - Fehler entstehen.
So auch bei Marleen aus dem Eingangsbeispiel, die bei der abschließenden Addition an der Zehnerstelle multipliziert, anstatt zu addieren. Möglicherweise handelt es sich dabei nur um einen Flüchtigkeitsfehler. Würde dieser Fehler aber wiederholt bei mehreren Aufgaben auftreten, müsste man im Unterricht überlegen, wie man Marleen beim Verständnis der schriftlichen Multiplikation helfen kann.
Die kreative Fehlstrategie von Marleen ist nicht die einzige denkbare Schwierigkeit, die bei der schriftlichen Multiplikation entstehen kann.
Im Folgenden geben wir Ihnen einen Überblick zu den Hürden und typischen Fehlern bei der schriftlichen Multiplikation (vgl. Padberg & Benz 2011, S. 278-283). Dieser bietet eine erste Grundlage, Fehler schneller zu erkennen, diese besser zu verstehen und somit entsprechende Fördermaßnahmen einzuleiten.
Häufig auftretende Schwierigkeiten sind z.B. (ROT: Stellen an denen der jeweilige Fehler erstmals sichtbar wird):
1. Fehler mit der Null
Fehlertyp: Einmaleinsfehler
0 ∙ a = a
Beispiel:
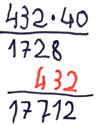
Fehlertyp: Einmaleinsfehler
a ∙ 0 = a
Beispiel:

Fehlertyp: Stellenwertfehler
Null im Multiplikator wird nicht beachtet
Beispiel:
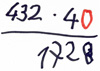
Fehlertyp: Stellenwertfehler
Null im Multiplikanden wird nicht beachtet
Beispiel:
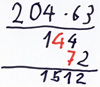
2. Fehler mit der Eins
Fehlertyp: Einmaleinsfehler
a ∙ 1 = 1
Beispiel:
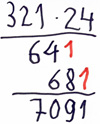
Fehlertyp: Stellenwertfehler
Die Teilprodukte werden falsch angeordnet oder unsauber aufgeschrieben: Ziffern stehen nicht stellengerecht untereinander
Beispiel:
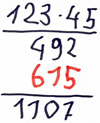
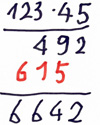
Fehlertyp: Übertragsfehler
Die Übertragsziffer wird als zusätzliche Ziffer im Teilprodukt notiert.
Beispiel:

Fehlertyp: Übertragsfehler
Einerziffer statt Zehnerziffer als Übertragsziffer notiert
Beispiel:
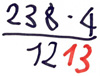
4·8=32, 3 aufschreiben, 2 merken
4·3=12, 12+2 =14, 1 aufschreiben, 4 merken...
Fehlertyp: Übertragsfehler
Überträge bei der Multiplikation vergessen
Beispiel:
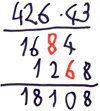
Fehlertyp: Übertragsfehler
Überträge bei der Addition vergessen oder falsch
Beispiel:

Fehlertyp: Übertragsfehler
Überträge werden aufgeschrieben und sind falsch.
Beispiel:
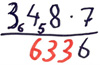
3. Einmaleinsfehler (unabhängig von Fehlern mit 0 und 1)
Fehlertyp: Einmaleinsfehler der Nähe
Ermitteln des Produkts über schrittweises Zählen und dabei +/- 1 Fehler bei der Anzahl der Teilschritte
Beispiel:

Fehlertyp: Einmaleinsfehler der Nähe
Ermitteln des Produkts über schrittweises Zählen und dabei +/- 1 Fehler bei einzelnen Additionen
Beispiel:

(vgl. Padberg & Benz 2011, S. 278-283)
Nun haben Sie schon einiges über Fehlertypen und Schwierigkeiten bei der schriftlichen Multiplikation erfahren.
Eigenaktivität
- Erfinden Sie selbst Aufgaben zur schriftlichen Multiplikation mit zwei- oder dreistelligen Zahlen, die möglichst schwer sind.
- Begründen Sie Ihre Auswahl.
Fehleranalyse
Eigenaktivität
Im Folgenden haben Sie nun anhand von Videos mit Schülerlösungen selbst die Möglichkeit, Schülerfehler zu identifizieren.
- Welche Teilschritte des Verfahrens beherrschen die Kinder schon sicher? Wo haben sie noch Schwierigkeiten?
- Ordnen Sie die Fehler, die Sie bei den Kindern im Video beobachten können, den Fehlertypen in der obigen Tabelle begründet zu.
- Wie würden Sie die verschiedenen Fehler im Unterricht thematisieren?
Alex 1
Kilian
Marleen
Alex 2
Sollten Sie Hilfe bei der Analyse benötigen, finden Sie hier eine beispielhafte Analyse.
Oben sehen Sie Einzelbeispiele zu den verschiedenen Fehlertypen. Wenn es jedoch darum geht, eine allgemeingültige Aussage über mögliche Fehlvorstellungen und Schwierigkeitsbereichen des Kindes zu machen, oder darum, einen Fehler bei einer bestimmten Aufgabe überhaupt zu verstehen, hilft einem häufig nur die Analyse mehrerer Aufgaben.
Auf der Seite Informative Aufgaben wird am Beispiel der schriftlichen Subtraktion verdeutlicht, dass es sehr hilfreich ist, sich mehrere, vergleichbare Aufgaben eines Kindes anzuschauen, um einen Fehler nachvollziehen zu können. Gleichzeitig sollte man sich stets bewusst machen, dass hinter einem Fehler allein noch keine Fehlvorstellung stecken muss.
Weiterführende Aufgaben
Eigenaktivität
Im Folgenden finden Sie noch weitere Schülerdokumente zur Analyse. Bearbeiten Sie auch hierfür die folgenden Arbeitsaufträge:
- Welche Teilschritte des Verfahrens beherrschen die Kinder schon sicher? Wo haben sie noch Schwierigkeiten?
- Ordnen Sie die Fehler, die Sie bei den Kindern im Video beobachten können, den Fehlertypen in der obigen Tabelle begründet zu.
- Wie würden Sie die verschiedenen Fehler im Unterricht thematisieren?
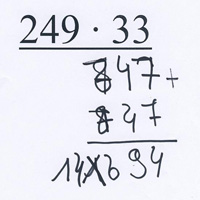
Chantal

Ibrahim
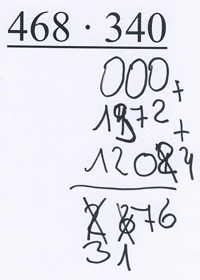
Bea
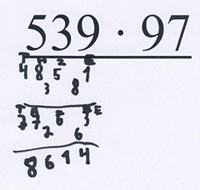
Kevin
Testen Sie Ihr Wissen zu dem Thema in unserem Kira-Check.
Verwandte Themen
Multiplikation und Division
Halbschriftliche Multiplikation
Schriftliche Subtraktion
Informative Aufgaben
Weitere Informationen zu einer auf Verständnis aufbauenden Einführung der schriftlichen Multiplikation finden Sie bspw. in dem Text von Höhtker & Selter (1998). Eine Vorversion diese Beitrages finden Sie im Selbststudiumsmodul unseres Partnerprojektes PIK AS: PIKAS: Selbststudium- Lernen auf eigenen Wegen: 'Von der halbschriftlichen zur schriftlichen Multiplikation'.
Materialien zum Thema 'Rechnen auf eigenen Wegen' sowie 'Vom halbschriftlichen zum schriftlichen Rechnen' finden Sie auf der Website des Projekts PIK AS, im PIKAS: Fortbildungsmodul: 'Lernen auf eigenen Wegen'.
Material
Interviewleitfaden
Literatur
