Die halbschriftliche Multiplikation ist ab dem 3. Schuljahr ein wichtiges Thema des Mathematikunterrichts. Die Kinder kennen zu diesem Zeitpunkt bereits die halbschriftlichen Vorgehensweise der Addition und Subtraktion und erschließen sich langsam den Zahlenraum bis 1000.
Auch bei der Multiplikation gibt es dabei verschiedene Vorgehensweisen und typische Fehler, mit denen sich diese Seite auseinandersetzt.
Die folgenden Ausführungen entstanden im Rahmen der Bachelorarbeiten von Hofemann & Rautenberg (2010) sowie Benner & Steinbach (2010).
Drittklässler rechnen die Aufgabe 16 · 15
Bereits vor der Thematisierung der Multiplikation von zwei zweistelligen Zahlen wurde Kindern des 3. Schuljahres die Aufgabe 16 · 15 gestellt. Dabei fielen u.a. die Vorgehensweisen von Lars und Kirsten auf.
Eigenaktivität
Analysieren und erläutern Sie die Vorgehensweisen beider Kinder. Überlegen Sie, welchen typischen Fehler Kirsten macht und wo möglicherweise die Ursache für diesen Fehler liegt bzw. was sich Kirsten dabei gedacht hat.
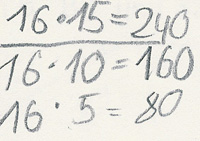
Lars
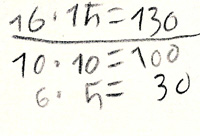
Kirsten
Hier finden Sie eine mögliche Erklärung.
Hintergrundwissen zum halbschriftlichen Rechnen
Das zentrale Kennzeichen des halbschriftlichen Rechnens ist die Zerlegung von komplizierten Aufgaben in leichtere Teilaufgaben. Es ist im Unterschied zu den Standardalgorithmen ein flexibles Rechnen, bei dem der Weg zur Lösung nicht vorgeschrieben ist, wobei die „Besonderheiten der vorliegenden Zahlen ausgenutzt" (Padberg & Benz 2010, S. 170) und jeweils passende Rechenstrategien eingesetzt werden.
Anders als beim Kopfrechnen werden hier die Zwischenschritte, Zwischenrechnungen und die Zwischenergebnisse schriftlich fixiert. Es zeichnet sich also durch die folgenden Charakteristika aus:
- Die Rechenwege sind beim halbschriftlichen Rechnen im Gegensatz zu den schriftlichen Algorithmen nicht vorgegeben.
- Die Art und Weise der Notation ist nicht festgelegt. Die Kinder notieren nicht unbedingt alle Teilschritte.
- Welche Lösungsstrategie aus der Sicht geübter Rechner sinnvoll oder weniger sinnvoll ist, hängt von den Zahlenwerten der jeweiligen Aufgabe ab.
Weitere Informationen zum Stellenwert des halbschriftlichen Rechnens finden Sie auf der Seite zur halbschriftlichen Addition.
Eigenaktivität
Lösen Sie die folgenden beiden Aufgaben halbschriftlich auf verschiedenen Wegen und beschreiben Sie jeweils Ihren Rechenweg. Finden Sie möglichst viele Strategien zum Lösen der Aufgaben.
- Aufgabe 1: 5 ∙ 44
- Aufgabe 2: 9 ∙ 19
Typische Vorgehensweisen bei der halbschriftlichen Multiplikation
Im Folgenden werden die Hauptstrategien der halbschriftlichen Multiplikation exemplarisch vorgestellt.
Die Auswertung der Studie im Rahmen der o.g. Bachelorarbeit zeigte, dass die Kinder meist sehr unflexibel im Umgang mit den unterschiedlichen Strategien sind und sich fast ausnahmslos auf die Strategie „Schrittweise" beschränken (ca. 75 % der Schüler). Oft kann man aber auch Mischformen der folgenden Strategien vorfinden:
1. Stellenweise
Beide Faktoren werden in ihre Stellenwerte zerlegt und können entweder als Teilaufgaben unter dem Strich oder im Malzeichen notiert werden. Die Teilergebnisse werden dann entweder nebeneinander oder untereinander addiert, um das Endergebnis zu erhalten.
Beispiel:
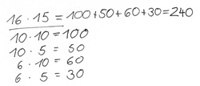
2. Schrittweise
Bei der Vorgehensweise „Schrittweise" wird nur ein Faktor in seine Stellenwerte zerlegt. Dies ist meist (aber nicht zwingend) der zweite Faktor, der dann schrittweise mit dem ersten Faktor multipliziert wird. Die Teilergebnisse werden anschließend addiert, um das Endergebnis zu erhalten.
Beispiel:
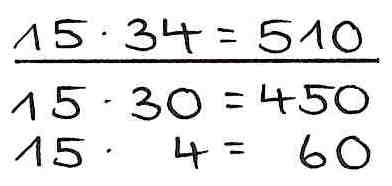
3. Vereinfachen
Bei der Anwendung der Strategie „Vereinfachen" werden beide Faktoren nach dem Gesetz der Konstanz des Produktes gegensinnig verändert: Verdoppelt/Verdreifacht/... man den einen Faktor, muss man den anderen halbieren/dritteln/usw. Nur so bleibt das Endergebnis unverändert.
Beispiel:
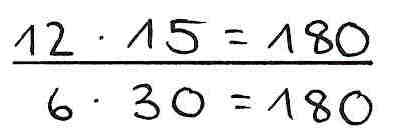
4. Hilfsaufgabe
Wendet man die Strategie „Hilfsaufgabe" an, notiert man sich zunächst als Nebenrechnung eine Hilfsaufgabe, die leichter zu berechnen ist als die vorgegebene. Aus dieser Nebenrechnung kann das Ergebnis dann abgeleitet werden. In der Regel wird bei dieser Strategie nur ein Faktor verändert.
Beispiel:
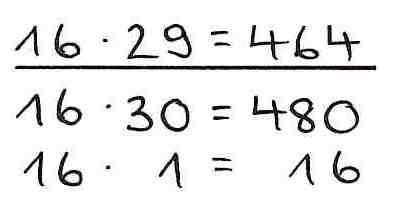
Eigenaktivität
Ordnen Sie Ihre eigenen Rechenwege der Aufgaben 5 ∙ 44 und 9 ∙ 19 in die halbschriftlichen Strategien ein und begründen Sie Ihre Zuordnung!
Ordnen Sie dann folgende Schülerlösungen den oben genannten Strategien zu!
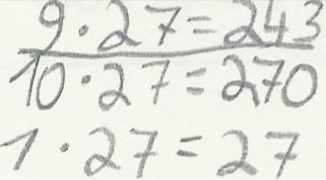
Leyla
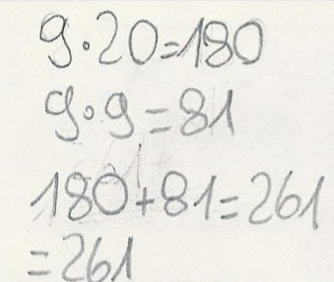
Meike
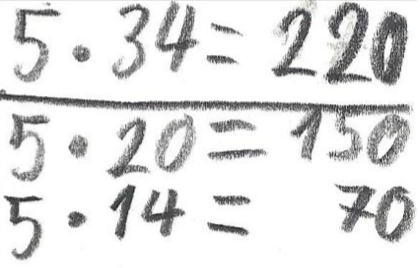
Anton
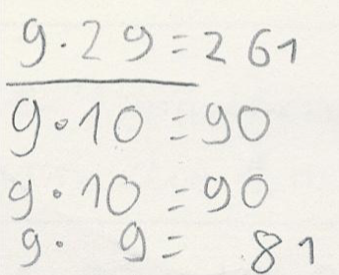
Nico
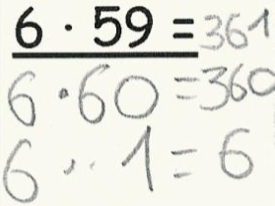
Dennis
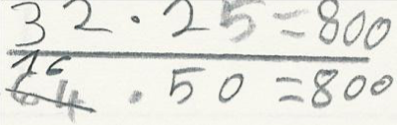
Alena
Welche Strategien haben die Kinder genutzt?
Hier finden Sie eine mögliche Zuordnung:
Lösungen Hauptstrategien halbschriftliche Multiplikation
Typische Fehler bei der halbschriftlichen Multiplikation
Jede Strategie birgt viele mögliche Fehlerquellen, die sich sowohl bei der Übertragung der Strategie auf verschiedene Aufgaben, als auch bei der Bearbeitung ergeben.
Benner & Steinbach (2010) haben im Rahmen ihrer Bachelorarbeit Kindern aus vierten Klassen Aufgaben zu halbschriftlichen Multiplikationsstrategien vorgelegt. Den Kindern wurde eine Strategie vorgegeben und an einem Beispiel erklärt. Jede Strategie wurde von jeweils ca. 60 Kindern bearbeitet und sollte auf drei weitere Aufgaben eigenständig übertragen werden.
Die entstandenen Schwierigkeiten und Probleme bei der Übertragung und Bearbeitung der einzelnen Strategien werden im Folgenden beispielhaft betrachtet.
Es ist bei vielen Schülerlösungen nicht immer möglich, einen eindeutigen Fehlertyp zu bestimmen. Um eine Fehlerauswertung vornehmen zu können, wurden die Fehler nach intensiver Analyse dennoch in Kategorien eingeteilt und die Dokumente entsprechend zugeordnet. Bei einigen Dokumenten wäre sicher auch die Zuordnung zu einer anderen Kategorie denkbar gewesen.
1. Verständnisfehler - nicht vollständige Ermittlung der Teilprodukte
Bei der stellenweisen Multiplikation müssen alle Stellenwerte des Multiplikanden mit denen des Multiplikators verrechnet werden. Das Ergebnis wird in diesem Beispiel nicht korrekt ermittelt, da ein Teilprodukt (20 ⋅ 6) nicht berechnet wird.
Beispiel:
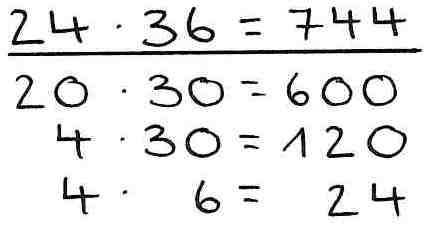
2. Verständnisfehler - ziffernweises Zerlegen der Faktoren
Der Multiplikand wird ausschließlich ziffernweise (in 2 und 6 statt 20 und 6) zerlegt, so dass die Teilprodukte auch ziffernweise berechnet werden. Folglich bleiben die Stellenwerte des Multiplikanden unberücksichtigt.
Beispiel:
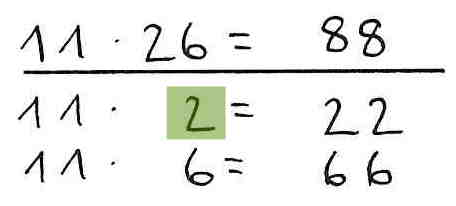
3. Verständnisfehler - gleichsinniges Verändern beider Faktoren
In diesem Beispiel wird das Gesetz von der Konstanz des Produktes nicht korrekt angewendet, da die beiden Faktoren gleichsinnig (⋅ 2) und nicht gegensinnig (15 ⋅ 2 und 12 : 2) verändert werden.
Beispiel:

4. Rechenfehler
In diesem Beispiel resultiert der Rechenfehler aus der fehlerhaften, nicht stellengerechten Notation der Zwischenergebnisse, sowie der anschließenden ziffernweisen Verrechnung der Teilprodukte.
Beispiel:
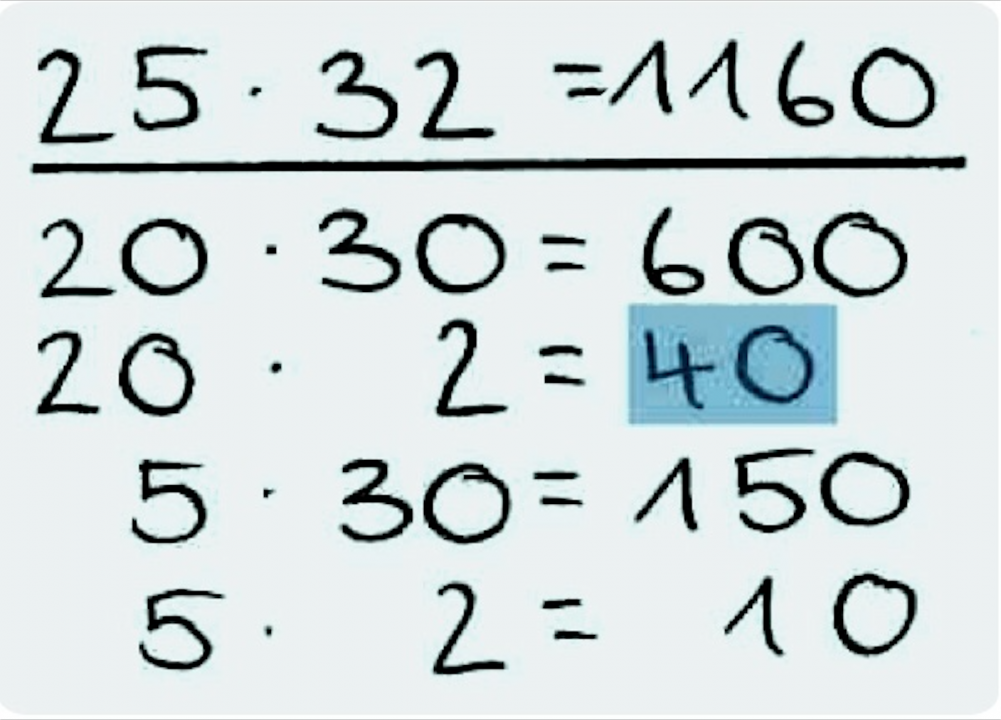
Eigenaktivität
Analysieren Sie die folgenden Schülerdokumente. Welche der o.g. Fehlertypen lassen sich beobachten? Welche Schülerdokumente lassen eine andere Deutung der Vorgehensweise zu? Begründen Sie.
Hier finden Sie eine mögliche Analyse der Schülerdokumente.
Schüler erklären Strategien anderer Schüler
Ziel des Unterrichts ist es nicht nur, dass die Kinder die einzelnen Strategien sicher anwenden können, sondern auch, ob und wie sie Lösungen anderer Schüler nachvollziehen und erklären können. Im Folgenden sehen Sie Beispiele, wie Kinder die Rechenwege anderer Kinder erklären.
Eigenaktivität
Analysieren Sie die Schülerdokumente. Welche Kinder verstehen die Beispiele und können sich ausdrücken, welchen Kindern fällt dies schwer? Warum ist das vielleicht so? Ordnen Sie die Kinder außerdem nach ihrem vermutlichen Leistungsstand!
Würden Sie ähnliche Aufgaben im Unterricht einsetzen? Nennen Sie Vor- und Nachteile von solchen Aufgaben und begründen Sie Ihre Antwort!
Florian:
Phillip:
Diana:
Lisa:
Hier finden Sie eine mögliche Analyse der Schülerdokumente:
Analyse der Schülerdokumente halbschriftliche Multiplikation
Testen Sie Ihr Wissen zu dem Thema in unserem Kira-Check.
Verwandte Themen
- Schriftliche Multiplikation
- Halbschriftliche Addition
- Halbschriftliche Subtraktion
- Halbschriftliche Division
Die meisten Erwachsenen kennen aus der Schule entweder nur die schriftlichen Rechenverfahren oder nutzen im Alltag intuitiv halbschriftliche Vorgehensweisen. Als Lehrperson mit dem Fach Mathematik sollten Sie allerdings die große Vielfalt halbschriftlicher Rechenverfahren kennen und im Unterricht mit Blick auf die individuellen Vorlieben der Lernenden die eine oder andere Strategie thematisieren. Das stellt fachfremd Unterrichtende vor eine große Herausforderung, da sie selbst in ihrer damaligen Schulzeit nur auf die schriftlichen Rechenverfahren eingetrimmt wurden.
Besuchen Sie deshalb die Homepage des Projekts PriMaKom („Primarstufe Mathematik kompakt“). Dabei handelt es sich in erster Linie um eine Selbstlernplattform für Lehrerinnen und Lehrer, die Mathematik fachfremd unterrichten und sich somit fachdidaktische Kenntnisse in kompakter Form aneignen möchten. Dort erhalten Sie kompakte Hintergrundinformationen sowie unterrichtspraktische Hinweise zu den halbschriftlichen Rechenstrategien: primakom: Inhalte: Zahlen und Operationen: Halbschriftliches Rechnen: Einstieg.
Material
Arbeitsblatt
Literatur
© Carina Benner, Lena Hofemann, Franziska Rautenberg und Maren Steinbach für das KIRA-Team
