Ähnlich wie die Geometrie im Mathematikunterricht der Grundschule oft vernachlässigt wird, finden sich in der Literatur auch nur wenige Beispiele zur Schulung der prozessbezogenen Kompetenzen im Umgang mit Raum und Form.
Im Rahmen ihrer Masterarbeit hat sich Angela Knappstein deshalb mit verschiedenen Aufgaben zur Schulung prozessbezogener Kompetenzen am Beispiel des Tangrams in den Klassen 3 und 5 auseinandergesetzt.
Auf der folgenden Seite stellt die Studentin ihre wesentlichen Ergebnisse vor und illustriert diese anhand ausgewählter Schülerdokumente, die im Zuge ihrer Arbeit entstanden sind.
Tangram - was ist das und wie lässt es sich einsetzen?
Das Tangram ist ein altes, chinesisches Legespiel, das aus je zwei großen und kleinen Dreiecken, einem Parallelogramm, einem Quadrat sowie einem mittlerem Dreieck besteht (vgl. Abbildung rechts).
Die folgenden Einstiegsaufgaben bieten Ihnen die Gelegenheit, sich mit dem Material vertraut zu machen. Auch soll Ihnen ein erster Hinweis auf die Einsatzmöglichkeiten des Tangrams im Geometrieunterricht zur Schulung der prozessbezogenen Kompetenzen gegeben werden.
Eigenaktivität
Erstellen Sie mithilfe der Vorlage ein eigenes Tangram.
- Welche Beziehungen bestehen zwischen den einzelnen Tangramteilen?
- Mit dem Tangram lassen sich die oben dargestellten Ziffern legen. Versuchen Sie diese nachzulegen. Finden Sie möglichst alle Möglichkeiten, das große Dreieck mit den anderen Tangramteilen auszulegen.
- Begründen Sie, warum das alle Möglichkeiten sind.
Hintergrundwissen
Einsatz des Tangrams im Geometrieunterricht
Der Geometrieunterricht ist heute unter dem Titel „Umgang mit Raum und Form" als eine der vier inhaltsbezogenen Kompetenzen fester Bestandteil des Mathematikunterrichts. Die folgende Tabelle stellt - angelehnt an den Mathematiklehrplan des Landes NRW (MSW NRW 2008, S. 63 ff.) - wesentliche Inhalte vor.
Umgang mit Raum und Form
Raumorientierung und Raumvorstellung
- Orientierung im zwei- und dreidimensionalen Raum
- Beschreibung und Nutzung räumlicher Beziehungen
Ebene Figuren
- Erkennen, Benennen und Untersuchen ebener Figuren
- Erstellen ebener Figuren
- Bestimmung und Vergleich von Flächeninhalt und Umfang
Körper
- Erkennen, Benennen und Untersuchen von Körpern
- Erstellen und Darstellen von Körpern und Körpermodellen
- Berechnung und Vergleich von Volumina
Symmetrie
- Erkennen, Überprüfen und Nutzen von Achsensymmetrie und Symmetrieeigenschaften
- Erzeugen komplexer symmetrischer Figuren
Zeichnen
- Zeichnen von Linien, Bögen, Figuren, etc. unter Nutzung von Hilfsmitteln wie Lineal, Schablone und Gitterpapier
Um diese Inhalte verständlich zu machen, bedarf es angebrachter Materialien. Das Tangram eignet sich hierbei besonders: Einerseits kann es - bis auf das Thema „Körper" - alle der oben genannten Inhalte ansprechen und andererseits von der ersten Klasse bis in die Sekundarstufe eingesetzt werden.
Dies entspricht dem Spiralprinzip, das besagt, dass bestimmte Themen, Materialien und Aufgaben über die Schuljahre hinweg immer wieder aufgegriffen, wiederholt und auf höherem Niveau vertieft werden sollen (vgl. z.B. Krauthausen & Scherer 2007, S. 138 f.). So können mit den geometrischen Grundfiguren, aus denen das Tangram besteht, Figuren und Muster aus- und nachgelegt, sowie selbst erstellt werden.
Dabei sind unterschiedliche Niveaustufen, beispielsweise durch Variation von verbaler und bildlicher Vorlage zu erreichen. Auch zeigen die Ziffern der Einstiegsaufgabe, dass Umrisse vorgegeben werden können. Ebenso kann - im Gegensatz zu der Ziffernaufgabe - die Originalgröße der Figur zur Erleichterung des Auslegens beibehalten werden.
Auf diese Weise stößt man aufgrund der Beziehungen unter den Teilen bei der Beschäftigung mit dem Tangram „zwangsläufig auf parallele Linien, Winkel, auf Figuren von verschiedener Form, aber gleichem Flächeninhalt bzw. umgekehrt" (Flechter 1965, S. 5), sowie auf Symmetrien. Weiterhin lassen sich sogar formale Sätze wie der "Satz des Pythagoras" herleiten und veranschaulichen.
Zudem ermöglicht das Tangram durch das Hantieren mit konkretem Material einen aktiv-entdeckenden Zugang zur Geometrie. Folglich ist eine „lebendige Auseinandersetzung mit der Mathematik" (KMK 2005, S. 7) und somit die Schulung der prozessbezogenen Kompetenzen zwangsläufig miteinbezogen (vgl. Walther u.a. 2005, S. 120).
Die Bedeutung prozessbezogener Kompetenzen
Dem Miteinbeziehen der prozessbezogenen Kompetenzen kommt eine besondere Bedeutung zu, da diese den „verständigen Erwerb inhaltsbezogener Fertigkeiten und Fähigkeiten" (MSW NRW 2008, S. 56) unterstützen und somit zum Erreichen „eines gesicherten Verständnisses mathematischer Inhalte" (KMK 2005, S. 6) entscheidend beitragen.
Sie beziehen sich auf den Prozess der aktiven Auseinandersetzung mit Mathematik und regen dadurch zur Reflektion der Lösungswege an. Auch wenn sie sich in der Unterrichtsrealität oft überschneiden (vgl. Walther u.a. 2005, S. 26), werden sie in der Literatur in gering unterschiedlichen Gewichtungen in vier bzw. fünf Schwerpunkte untergliedert.
Im Folgenden sollen diese durch ein Beispiel aus der Kompetenz „Raum und Form", schwerpunktmäßig auf das Tangram bezogen, erläutert werden.
Die Kompetenz Problemlösen/ kreativ sein wird durch solche Aufgaben angesprochen, die dazu auffordern „eine Lösung zu finden, ohne dass ein passendes Lösungsverfahren auf der Hand liegt" (Büchter & Leuders 2005, S. 28).
So können die Kinder unter Nutzung von Zusammenhängen eigene Lösungsstrategien entwickeln, diese nutzen, auf Angemessenheit hin überprüfen und auf ähnliche Sachverhalte übertragen.
Dies ist beispielsweise beim Auslegen eines gegebenen Umrisses mit allen Tangramteilen der Fall, da hier nicht vorgegeben ist, wie die Kinder vorgehen sollen. Außerdem zählt das Variieren und Erfinden von Aufgaben zu dieser Kompetenz. Ein Beispiel wäre hier, eigene Figuren als Rätsel für andere Kinder legen zu lassen.
Unter Modellieren wird verstanden, Sachsituationen relevante Informationen zu entnehmen, diese mithilfe eines mathematischen Modells zu berechnen (mathematisieren) und die so erzielten Ergebnisse wieder auf die Sachsituation zurück zu beziehen. Es geht also vor allem um die Umwelterschließung mithilfe der Mathematik.
Dies ist mit dem Tangram schwer zu erreichen. Im Geometrieunterricht allgemein könnte hier aber zum Beispiel die Anzahl der Fahrzeuge, die in einem 100m langen Stau stehen, mit Hilfe von Bögen aus Kästchenpapier realitätsnah berechnet werden (vgl. Walther u.a. 2005, S. 122 f.).
Das Argumentieren meint, Vermutungen über mathematische Zusammenhänge und Auffälligkeiten anzustellen, auf Korrektheit zu prüfen sowie aus singulären Erfahrungen zunehmend allgemeine Überlegungen zu entwickeln, nachzuvollziehen und zu erläutern.
Bezogen auf das Tangram kann man zum Beispiel alle Möglichkeiten, eine Figur auszulegen, finden lassen. Hierbei kann man begründen lassen, warum alle Möglichkeiten gefunden sind.
Schließlich beinhaltet die Kompetenz Darstellen/Kommunizieren die Fähigkeiten, Aufgaben kooperativ zu lösen, Vorgehensweisen und Ergebnisse unter Nutzung verschiedener Darstellungsformen (zeichnerisch, schriftlich, unter Nutzung von Tabellen, etc.) angemessen zu dokumentieren sowie zu präsentieren und dabei zunehmend Fachsprache zu verwenden.
So kann das Erstellen einer Anleitung zum Auslegen einer vorgegebenen oder selbst erfundenen Figur als Beispiel genannt werden.
Eigenaktivität
Betrachten Sie nochmals die vierte Einstiegsaufgabe.
Welche prozessbezogenen Kompetenzen werden angesprochen? Welche nicht? Begründen Sie Ihre Entscheidung!
Schülerdokumente analysieren
Eigenaktivität
Im Rahmen ihrer Masterarbeit hat Knappstein (2011) Kindern des dritten und fünften Schuljahres die vierte Einstiegsaufgabe gestellt. Analysieren Sie die nachfolgenden Schülerdokumente:
- Begründen Sie, inwiefern sich die Lösungen der Grundschüler von denen der Fünftklässler unterscheiden?
- Welche prozessbezogenen Kompetenzen sind in den einzelnen Dokumenten zu finden?
Drittklässler
Jannik
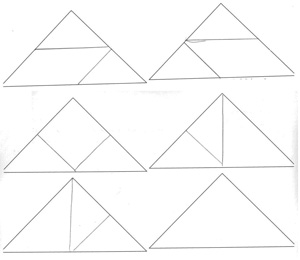

Frederike
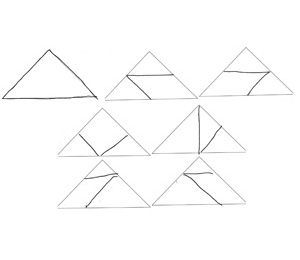

Julia
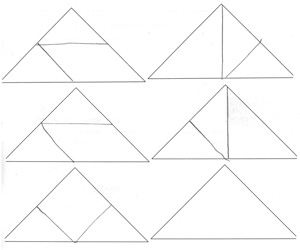

Frauke
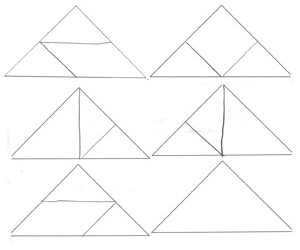

Fünftklässler
Christoph
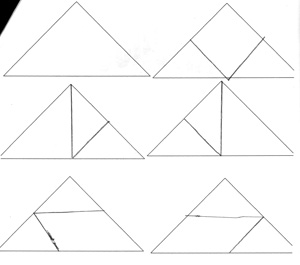

Micha
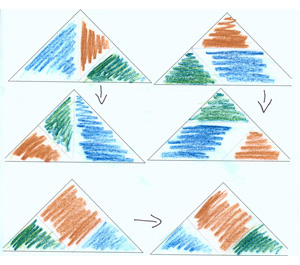

Nikolas
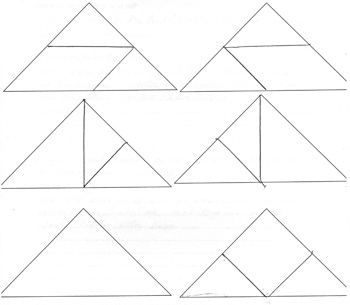

Anna
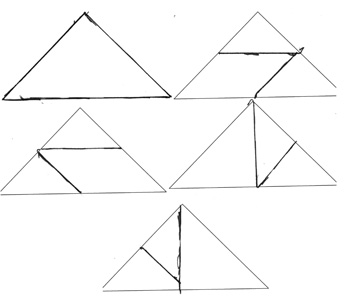

Weiterführende Aufgaben
Eigenaktivität
Trotz der oben genannten Vorteile, ist das Tangram ein Material und somit auch „Lerngegenstand mit eigenen Anforderungen für die Schülerinnen und Schüler, die [dessen] Bedeutungen und Formen des Gebrauchs erlernen müssen" (MSW NRW 2008, S. 55). Dies bedeutet, dass die Kinder zuerst mit dem Material vertraut werden müssen, bevor sie es zum Lernen geometrischer Inhalte nutzen können.
- Überlegen Sie, wie Sie vor diesem Hintergrund das Tangram im Unterricht einführen könnten.
- Finden Sie weitere Aufgaben, die die prozessbezogenen Kompetenzen in der Geometrie unter Einsatz des Tangrams fördern.
Hier finden Sie eine Liste weiterer denkbarer Aktivitäten am Tangram:
Tangram: weitere denkbare Aktivitäten
Verwandte Themen
Kompetenzen im Mathematikunterricht
Achsensymmetrie
Weitere Informationen zu der inhaltbezogenen Kompetenz „Raum und Form" finden Sie im Mathematiklehrplan für das Land NRW sowie in den Bildungsstandards.
Material
Arbeitsblatt Tangram
Literatur
© Angela Knappstein für das KIRA-Team
