Das Leben in einer dreidimensionalen Welt verlangt es, räumliche Gegebenheiten wahrzunehmen, diese in der Vorstellung zu „sehen", sie mental zu bewegen und umzusortieren. Diese Fähigkeiten können allerdings nicht als selbstverständlich vorausgesetzt werden. Vielmehr durchlaufen sie insbesondere im Grundschulalter einen Entwicklungsprozess, der durch geeignete Lernanlässe angeregt und gefördert werden muss.
Auf dieser Seite wird exemplarisch gezeigt, wie das Raumvorstellungsvermögen mit Hilfe des Aufgabenformats "Würfelnetze" in der Grundschule gefördert werden kann.
Kinder suchen Quadratsechslinge
In einem dritten Schuljahr wurde eine Unterrichtseinheit zum Thema "Würfelnetze" durchgeführt (vgl. Gatzka & Jungblut 2010). Als Einstieg in das Thema bekamen die Kinder den Forscherauftrag, möglichst viele Quadratsechslinge zu finden, die sich zu einem Würfel zusammenfalten lassen. Die offene Aufgabe ermöglichte den Schülerinnen und Schülern eine Bearbeitung entsprechend ihres individuellen Niveaus, sodass ganz unterschiedliche Ergebnisse entstanden sind:



Eigenaktivität
1. Haben die Kinder einige oder auch alle Würfelnetze gefunden?
2. Wo sehen Sie Fehler? Wie würden Sie damit im Unterricht umgehen?
3. Welche Impulse zur Weiterarbeit geben Sie diesen Kindern?
Hintergrundwissen zu Raumvorstellung und Würfelnetzen
Raumvorstellung
Menschen können die räumliche Umwelt wahrnehmen und sich in dieser orientieren. Sie sind befähigt, einen Ball zu fangen, Wege in der Vorstellung zu beschreiben sowie Gegenstände platzsparend in einen Schrank einzusortieren.
Diese Fähigkeiten werden alle durch räumliche Fähigkeiten bedingt, die sich nach Franke (2006) aus den Bereichen visuelle Wahrnehmung, räumliches Vorstellungsvermögen und räumliches Denken zusammensetzen. Die visuelle Wahrnehmung wird als das konkrete Operieren mit vorhandenen Objekten im dreidimensionalen Raum definiert (vgl. Franke 2006, S. 52).
Wesentlich für die Entwicklung visueller Fähigkeiten sind demnach Handlungserfahrungen am Material. So können an Arbeitsmitteln Vorstellungen konkret entwickelt werden, indem Lernende die geometrischen Objekte im wahrsten Sinne „begreifen".
Dabei entstehen aus den sinnlich registrierten Reizen Vorstellungsbilder, die mental abgespeichert, verändert und zueinander in Beziehung gesetzt werden können.
Die visuelle Wahrnehmung stellt die notwendige Voraussetzung für die Raumvorstellung dar, da Raumvorstellungsvermögen als "die Fähigkeit mental mit geometrischen Objekten zu operieren" definiert wird. Operationen wie Transformationen von Objekten/Objektteilen oder räumliche Bewegungen wie Drehungen, Verschiebungen und Faltungen erfolgen rein in der Vorstellung.
Empirisch belegt ist, dass sich das Raumvorstellungsvermögen im Alter von sieben bis dreizehn Jahren besonders stark entwickelt (vgl. Radatz & Rickmeyer 1991, S. 145).
Folglich kommt der Behandlung geometrischer Inhalte zur Förderung der räumlichen Fähigkeiten insbesondere in der Grundschule eine wesentliche Bedeutung zu (vgl. MSW NRW 2008, S. 58).
So kann das Raumvorstellungsvermögen der Kinder durch geeignete geometrische Inhalte im Mathematikunterricht gefördert werden. Ausgehend von konkreten Operationen am Material können so mit der Zeit in einem kontinuierlichen Verinnerlichungsprozess mentale Vorstellungsbilder entstehen, mit denen die Kinder mental flexibel operieren können.
Eine Möglichkeit, das Raumvorstellungsvermögen der Schüler zu fördern, stellt die unterrichtliche Behandlung von Würfelnetzen dar, anhand derer die Schüler charakteristische Eigenschaften von Würfelnetzen entdecken, die Beziehungen von Ebene und Raum verdeutlichen und ihr Raumvorstellungsvermögen schulen können.
Dies wird im Folgenden exemplarisch an einer Aufgabe zum Thema "Würfelnetze" aus einer Lernumgebung von Gatzka & Jungblut (2010) veranschaulicht.
Würfelnetze
Mathematisch gehören Würfelnetze zu den Hexominos, da sie aus sechs zusammenhängenden Quadratflächen bestehen. Sind diese Flächen so angeordnet, dass sie sich zu einem Würfel zusammenfalten lassen, werden sie als Würfelnetze bezeichnet. Würfelnetze können hergestellt werden, indem die sechs Flächen zu einem Netz zusammengesetzt, der Körper abgewickelt oder an den Kanten aufgeschnitten wird (vgl. Radatz & Schipper 1991, S. 162).
In der unten dargestellten linken Abbildung handelt es sich um ein solches Würfelnetz, da man dieses Körpernetz zu einem Würfel zusammenfalten kann, wie die weiteren Abbildungen zeigen.
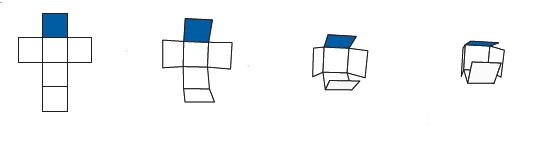
(Huhmann 2006)
Eigenaktivität
Es gibt noch weitere Würfelnetze.
Versuchen Sie zunächst selbst, alle weiteren möglichen Würfelnetze zu finden.
Hier finden Sie alle möglichen Würfelnetze.
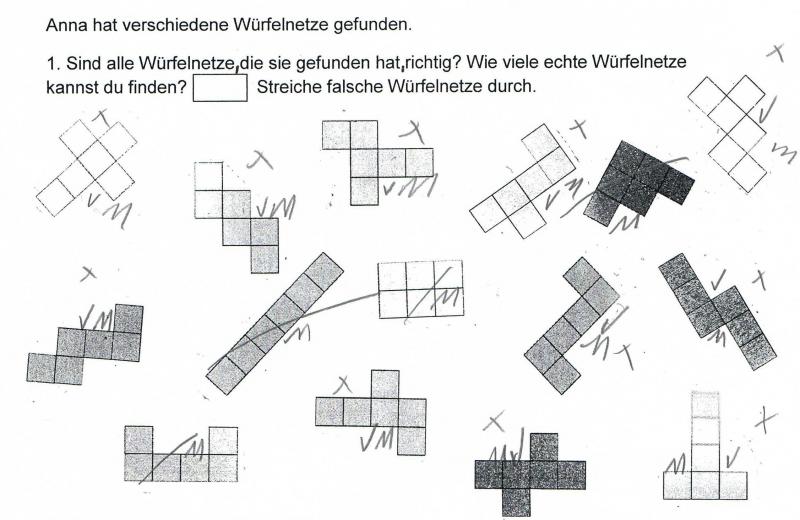
Wie viele echte Würfelnetze kannst du finden?
Nachdem die Kinder selbstständig Würfelnetze entdeckt haben, wurde ihnen folgende „Anna-Aufgabe" gestellt:
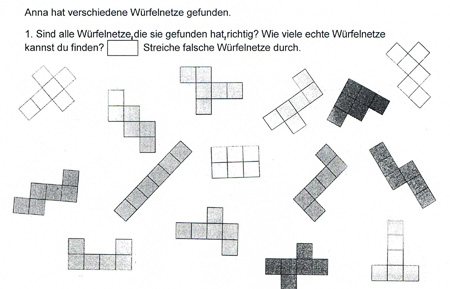
Die Kinder sollen zunächst überprüfen, ob es sich bei allen gefundenen Netzformen um richtige Würfelnetze handelt und mit M (für „mit Material gelöst") und mit K (für „im Kopf gelöst") kennzeichnen, wie sie die einzelnen Netzformen überprüft haben.
Die Aufgabe ermöglicht eine niveaudifferenzierte Bearbeitung, die einen Wechsel der Vorgehensweisen von Netz zu Netz zulässt.
- So können sich die Schülerinnen und Schüler zum einen ihres visuellen Gedächtnisses bedienen, indem sie sich an einige der Würfelnetze aus den vorangegangenen Stunden erinnern.
- Zum anderen können sie die Netzformen mithilfe des Materials überprüfen. Das Material hat die Funktion, den Wechsel zwischen Ebene und Raum zu verdeutlichen. Die Schüler nutzen es, um Netzformen auszuprobieren oder um Ideen zu überprüfen.
- Des Weiteren kann die Identifizierung der richtigen und falschen Netzformen mental erfolgen. In diesem Fall falten die Kinder die Netzformen gedanklich zusammen und vollziehen somit räumliche Bewegungen von der Ebene zum Raum in der Vorstellung.
Eigenaktivität
Betrachten Sie die ausgewählten Schülerdokumente (für eine größere Ansicht klicken Sie auf das jeweilige Kinderdokument).
- Was fällt Ihnen auf?
- Welche Würfelnetze überprüfen die Kinder eher im Kopf? Welche eher mit Material? Woran kann das liegen?
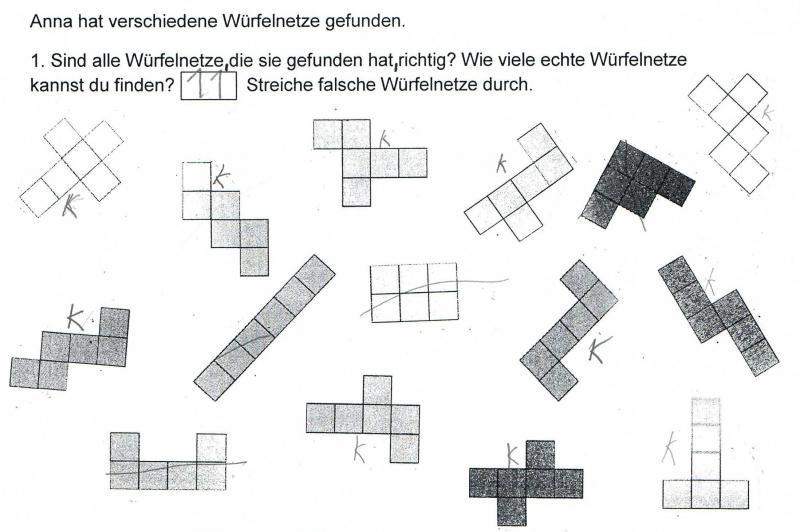
Serhat
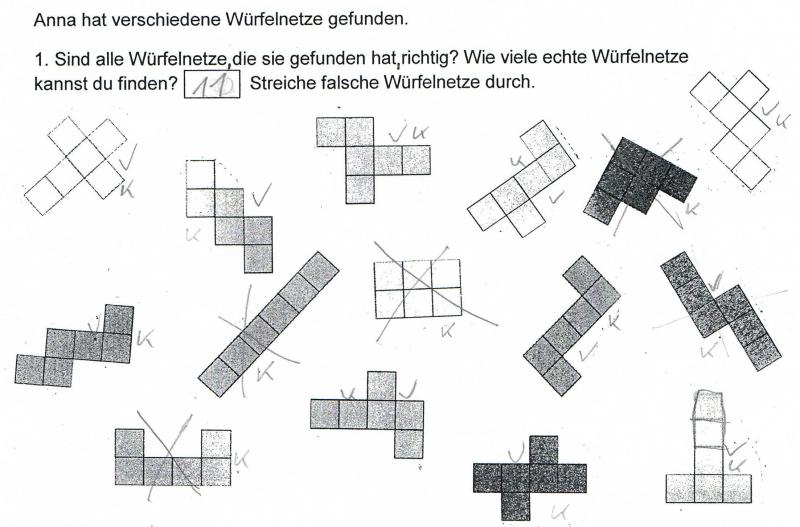
Kay
Drita

Athiksha
Hier finden Sie eine Zusammenfassung einiger Auffälligkeiten.
Eigenaktivität
Der ergänzende Arbeitsauftrag „Erkläre Anna, warum die anderen Netze keine echten Würfelnetze sind" diente vordergründig dazu, auch die prozessbezogenen Kompetenzen anzusprechen.
Des Weiteren ermöglicht die Aufgabe einen Einblick, inwiefern die Kinder bereits Kriterien oder Regeln ausgebildet haben, die ihnen die Identifizierung der Netze erleichtern. So ermöglichen ausgebildete Fähigkeiten der visuellen Wahrnehmung das Erkennen von Ähnlichkeiten und Unterschieden der Netzformen und somit das Ausmachen störender Netzflächen sowie das Vornehmen von Korrekturen.
Bevor Sie sich die Erklärungen der Kinder anschauen, versuchen Sie zunächst die folgenden beiden Fragen zu beantworten:
Wie würden Sie „Anna" erklären, dass einige ihrer gefundenen Lösungen keine echten Würfelnetze sind?
Was würden Sie von Drittklässlern als schriftliche Erklärung erwarten?
Betrachten Sie anschließend die folgenden Kinderlösungen, vergleichen Sie diese und stellen Sie Gemeinsamkeiten und Unterschiede heraus. Versuchen Sie auch, unterschiedliche Niveaus in den Begründungen der Kinder zu finden.

Aylin

Beyza

Blinera

Denis

Maxi

Maik
Hier finden Sie eine mögliche Einordnung der Kinderlösungen.
Die Auswahl an Schülerdokumenten verdeutlicht, wie stark die Schülerlösungen inhaltlich variieren können. Diese Unterschiede lassen sich sowohl auf sprachliche als auch auf bereits entwickelte räumliche Fähigkeiten zurückführen. Eine kompetenzorientierte, kriteriengeleitete Form der Begutachtung erscheint demnach als unabdingbar.
Weiterführende Aufgabe
Ihnen ist bei der Betrachtung der Schülerlösungen sicherlich aufgefallen, dass sich den Schülerdokumenten sowohl quantitativ als auch qualitativ sehr unterschiedliche Informationen entnehmen lassen.
Betrachten Sie folgendes Dokument von Merve kompetenzorientiert.
- Verstehen Sie, wie Merve denkt. Welche Kompetenzen sehen Sie bei ihr?
- Sicherlich hat Merve noch große sprachliche Schwierigkeiten, ihre Gedankengänge entsprechend auszudrücken. Wie könnten Sie in einem mündlichen Gespräch mit Merve (beispielsweise im Rahmen einer Kindersprechstunde) herausfinden, ob Merve noch weitere Kompetenzen zeigt?

(Merve bezieht sich auf das falsche Würfelnetz, bei dem sich sechs Quadrate in einer Reihe befinden. Sie schreibt: "Ersten mall ist das Material falsch weil die Grante ist dan ka man nischt wuvel machen. weil die das Grante. Wen ich das zu klamde dan nemden ist Lüge ist.")
Hier finden Sie eine mögliche kompetenzorientierte Betrachtung.
Verwandte Themen
Achsensymmetrie
Tangram
Ausführliche Informationen zur Entwicklung und Bedeutung des Raumvorstellungsvermögens finden Sie beispielsweise in:
Franke, M. (2006). Didaktik der Geometrie in der Grundschule (2. Aufl.). Heidelberg: Spektrum Akademischer Verlag.
Maier, P.H. (1999). Räumliches Vorstellungsvermögen. Ein theoretischer Abriß des Phänomens räumliches Vorstellungsvermögen. Donauwörth: Auer.
Auf der Website unseres Partnerprojekts PIK AS finden Sie im PIKAS: Unterrichtsmodul: Raum und Form: 'Würfelnetze' neben weiteren Informationen auch Unterrichtsmaterial zum Thema 'Würfelnetze'.
Weitere Anregungen zum Thema 'Lernstände wahrnehmen' bietet das Fortbildungsmodul des Projekts (PIKAS: Fortbildungsmodul: Lernstände wahrnehmen).
Material
Arbeitsblatt "Anna-Aufgabe"
Literatur
