Lernumgebungen wie „figurierte Zahlenfolgen", ermöglichen Kindern eine Auseinandersetzung mit mathematischen Inhalten auf ihrem individuellen Niveau.
Bei der Untersuchung der Zahlenfolgen auf Regelmäßigkeiten oder der Bestimmung der 20. Folgezahl bieten sich den Kindern zahlreiche Anlässe zum Ausprobieren und Erforschen sowie zum Aufstellen, Überprüfen und schließlich auch zum Begründen von Thesen über Zusammenhänge und Bildungsgesetze.
Im Folgenden sollen Bearbeitungsstrategien von Fünftklässlern vorgestellt werden, bevor Sie die Möglichkeit erhalten, sich mit einem typischen Fehlermuster zu beschäftigen. Abschließend werden einige Schülerdokumente hinsichtlich der Begründungskompetenz der Schüler verglichen.
Die Ausführungen auf dieser Seite werden mit Kinderdokumenten von Fünftklässlern illustriert, die im Rahmen der Bachelorarbeit von Anne Smirek (2012) entstanden sind.
"Klötzchenbaufolge" und "Treppenaufstieg"
Diese und viele andere kreative Namen werden für die berühmten Folgen geometrischer Zahlen - Quadratzahlen und Dreieckszahlen - von Kindern vorgeschlagen. So wird der Einstieg ins Thema jedem Kind ermöglicht, denn der Kreativität sind bei der Namensgebung keine Grenzen gesetzt.
Eine Einführung ins Aufgabenformat am Beispiel von Quadratzahlen (=„Klötzchen-aufbaufolge) und Dreieckszahlen (=„Treppenaufstieg"):
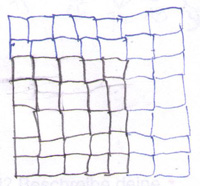
Der Name „Quadratzahlen" ergibt sich aus der folgenden geometrischen Darstellung:
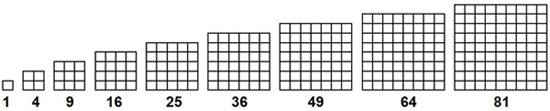
Beispiele für berühmte Folgen geometrischer Zahlen sind neben den Quadratzahlen auch die Dreieckszahlen (im Folgenden auch „Treppen" genannt). Hier sehen Sie die ersten drei Dreieckszahlen:
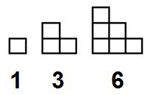 u.s.w.
u.s.w.
Eigenaktivität
- Setzen Sie die Zahlenfolge bis zur 10. Folgezahl fort. Reflektieren Sie hierbei ihre Strategie: Wie haben Sie jeweils die nächste Folgezahl bestimmt?
- Versuchen Sie nun die 20. Folgezahl zu bestimmen. Wie begründen Sie Ihre Lösungsstrategie? Fallen Ihnen weitere Möglichkeiten ein, die 20. Folgezahl zu ermitteln?
- Vergleichen Sie Ihre Lösungswege mit denen Ihrer Kommilitoninnen und Kommilitonen bzw. Kolleginnen und Kollegen. Gab es unterschiedliche Strategien?
- Im Kap. „Das Aufgabenformat" finden Sie Lösungshinweise und den mathematischen Hintergrund zu dieser Aufgabe.
- Im Kap. „Hauptstrategien" können Sie Ihre Lösung einer der drei Hauptstrategien zuordnen.
Hintergrundwissen
Das Aufgabenformat
Figurierte Zahlen (auch „Folgen geometrischer Zahlen") kann man auf unterschiedliche Arten darstellen: Figuriert durch geometrische Formenmuster und symbolisch durch die jeweils zugehörigen Zahlenfolgen.
(i) Figuriert: Formenmuster
Die Zahlenfolge entwickelt sich aus einer Folge wachsender, ähnlicher Figuren. Alle Figuren der Folge haben gemeinsame Merkmale, die sie verbinden (s. Bildungsgesetze).
Um die Folge fortzusetzen, müssen diese Merkmale erkannt und auf neue Folgeglieder übertragen werden.
Beispiel: Bei den T-Formen entsteht die nächste Figur
durch Verlängerung aller drei „Arme" um genau einen Stein.
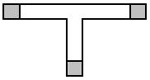
(ii) Symbolisch: zugehörige Zahlenfolgen
Diese abstraktere Darstellung der Zahlenfolge ergibt sich durch die Bestimmung der Kästchenanzahl der jeweiligen Figuren der Folge.
Die symbolische Zahlenfolge wird am besten deutlich, wenn man die Anzahl der Kästchen, abhängig von der Position der entsprechenden Figur innerhalb der Folge, ordnet. Hierzu kann man sie zum Beispiel in eine geeignete Tabelle eintragen:
Position der Figur: 1 2 3 4 5 6 7 8 9 10 ...
Anzahl der Kästchen:
Bildungsgesetze:
Die gemeinsamen Merkmale, die die einzelnen Figuren einer figurierten Folge verbinden, resultieren in folgespezifischen Bildungsgesetzen.
Hier ein kurzer Überblick über die figurierten Zahlenfolgen, deren Bearbeitung durch Schüler auf dieser Seite vorgestellt werden soll:
Dreieckszahlen/ "Treppen"
Explizite Darstellung: Dn=1/2 n (n+1) Dn=1+2+3+...+n
Rekursive Darstellung: Dn=Dn-1+n
Figurierte Folge: 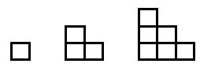
Quadratzahlen
Explizite Darstellung: Qn=n2 Qn=1+3+5+....+(2n-1)
Rekursive Darstellung: Qn=Q(n-1)+(2n-1)
Figurierte Folge: 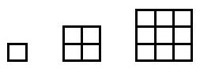
T-Form
Explizite Darstellung: Tn=1+3n Tn=1+3+3...+3
(n mal 3 addieren)
Rekursive Darstellung: Tn=Tn-1+3
Figurierte Folge: 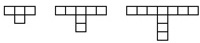
Die Lernumgebung "figurierte Zahlenfolge"
Potenzial der Lernumgebung
Die Auseinandersetzung mit figurierten Zahlenfolgen fördert die prozessbezogenen Kompetenzen der Schüler. Beim Lösen der Aufgaben werden die Problemlöse-Fähigkeiten der Kinder angesprochen, da es keinen vorgeschriebenen Lösungsweg gibt und die Kinder über ihr Vorgehen selbst entscheiden können.
Die Darstellung der Lösungswege, zum Beispiel durch die Präsentation vor der Klasse an der Tafel oder durch eine Diskussion im Stuhlkreis, schult die kommunikativen sowie die darstellerischen Kompetenzen der Schülerinnen und Schüler.
Die Lernumgebung bietet die Chance, sowohl leistungsstarke als auch leistungsschwächere Kinder im Sinne der natürlichen Differenzierung zu fördern und zu fordern (vgl. Hengartner/Hirt/Wälti 2006, S.11).
Durch geringfügige Variationen der Figuren lassen sich leicht eine Vielzahl von weiteren analogen Figurenfolgen - auf jeweils unterschiedlichen Anforderungsniveaus - finden.
Hier können Kinder auf ihrem individuellen Leistungsniveau viele Entdeckungen machen:
Während langsamere Rechner damit beschäftigt sind, die Merkmale der Zahlenfolgen zu erkennen und zum Fortsetzen der Folge zu nutzen, können besonders begabte Kinder diese Merkmale und Regelmäßigkeiten vielleicht schon begründen. Das Fortsetzen der Zahlenfolge kann durch unterschiedliche Strategien auf unterschiedlichen Abstraktionsniveaus geschehen (vgl. Kap. 3 Hauptstrategien).
Auch ist vorstellbar, dass die Lernenden selber Figurenfolgen erstellen, die dann von ihren Mitschülern untersucht werden können. Damit auch die jeweiligen „Erfinder" selbst möglichst viel mathematisch profitieren, können sie Musterlösungen erstellen, die für die anderen Kinder dann zur Kontrolle dienen.
Anknüpfungspunkte im Mathematikunterricht anderer Jahrgangsstufen
Da die explizite Berechnung von Zahlen der Zahlenfolge ein fundiertes Grundwissen und eine sichere Anwendung aller vier Grundrechenoperationen erfordert, erscheint die Behandlung des Themas ab der 4. Klasse aufwärts sinnvoll.
Eine Steigerung der Schwierigkeit ist ohne Probleme möglich, sodass auch höhere Jahrgangsstufen an Zahlenfolgen forschen können. Im Sinne des spiralförmigen Unterrichts kann das Thema also in höheren Klassenstufen wieder aufgegriffen und so vertieft werden:
5.-6. Schuljahr:
Eine konkrete Möglichkeit hierzu wird in dem Werk „Lernumgebungen für Rechenschwache bis Hochbegabte" (vgl. Hengartner u. a 2006, S. 127ff) unter dem Titel „Mit Würfeln bauen und Zahlenfolgen beschreiben 5-6" vorgestellt. Im Rahmen dieser Lernumgebung werden figurierte Zahlenfolgen, die durch komplexe dreidimensionale Bauten dargestellt werden, untersucht.
2.-4. Schuljahr:
Der Thematisierung von figurierten Zahlenfolgen kann die Behandlung von Folgen ohne geometrischen Bezug vorangehen. Auch hier sind Schüler dazu herausgefordert, Bildungsgesetze zu erkennen und Folgen fortzusetzen (vgl. Selter 1999, S. 10ff). Auf visuelle Unterstützung müssen die Lernenden bei diesem Aufgabenformat allerdings verzichten.
Hauptstrategien: Abzählen, Rekursiv, Explizit
Im Folgenden werden die Hauptstrategien zur Bestimmung der symbolischen Darstellung von Folgezahlen vorgestellt.
Hierzu werden Kinderdokumente, die aus der Bearbeitung zweier verschiedener Aufgabentypen stammen, zur Illustration bereitgestellt. Bearbeitet wurden jeweils die drei Folgen: Quadratzahlen, „T Form", Dreieckszahlen.
1. Aufgabentyp:
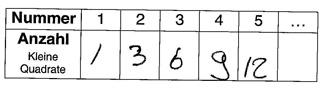
Wie viele kleine Quadrate haben die Figuren?
Trage in die Tabelle ein.
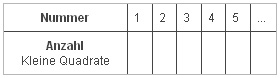
Welche Regelmäßigkeiten fallen dir auf? Beschreibe deine Beobachtungen!
(entsprechende Abbildung)
Bsp. Quadratzahlen:

2. Aufgabentyp:
Wie viele kleine Quadrate hat wohl die 20. Figur?
Hier ist Platz für deine Überlegungen:
Erklärung:
Die Auswertung der Kinderdokumente im Rahmen o.g. Bachelorarbeit zeigt, dass die Lösungsstrategien der Kinder stark von der jeweiligen geometrischen Folge abhängen.
So favorisierten die Kinder bei der Ermittlung der Quadratzahlen die explizite Berechnung, während bei der Berechnung der Folgezahlen der Dreieckszahlen fast ausschließlich rekursiv vorgegangen wurde. Bei der T-Form wurden beide Strategien in etwa gleich oft verwendet. Die Ermittlung der Zahlen durch Abzählen der Kästchen der zuvor gezeichneten entsprechenden Figur wurde von den Kindern im Vergleich zu den anderen zwei Strategien verhältnismäßig selten gewählt.
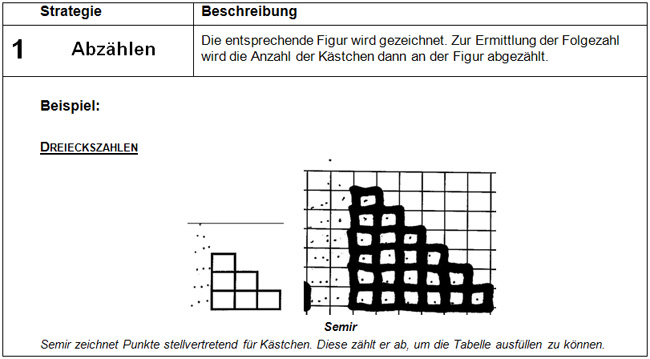

Die Lösungen der Kinder sind nicht immer gleich verständlich. Manchmal muss man sich etwas Zeit nehmen, um die Denkwege der Kinder nachzuvollziehen.
Eigenaktivität
- Sehen Sie sich Ihre Lösung zur Einführungsaufgabe in Kap. 1 an. Haben Sie eine der vorgestellten Hauptstrategien genutzt? Für welche Strategie haben Sie sich entschieden?
- Versuchen Sie die folgenden Kinderdokumente einer der drei Strategien zuzuordnen.
QUADRATZAHLEN:
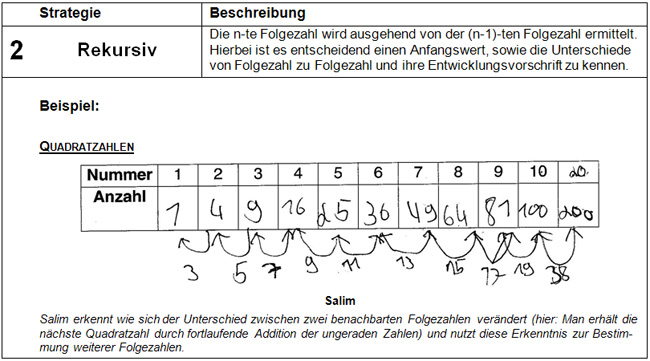
Salim (zur Tabelle)

Luis (20. Folgezahl)

Luis (zur Tabelle)
T-FORM:

Orca (20. Folgezahl)

Mathis (wenn man von 10 auf 20 hoch rechnen soll und das erste mal plus 1 rechnet enthält jede Zahl 3 Quadrate. Das geht dann immer so weit bis 20.)
DREIECKSZAHLEN:

Pia (zur Tabelle)
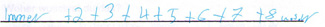
Frank (Begründung, 20. Folgezahl)
Hier finden Sie eine Zuordnung der Kinderlösungen zu den einzelnen Strategien.
Ein typischer Fehler
Wenn Fehler nicht auf Flüchtigkeit beruhen, sondern ihnen Fehlvorstellungen zugrunde liegen, lohnt sich ein zweiter Blick. Gelingt es der Lehrerin, den Grund für das Auftreten eines charakteristischen Fehlers aufzudecken, dann hat sie einen Ansatzpunkt für eine gezielte Förderung zur Überwindung der Fehlvorstellungen.
Bei der Auswertung der Zahlenfolgen-Aufgaben stach besonders ein Fehlertyp heraus.
Er trat sowohl in der Bearbeitung aller drei untersuchten Zahlenfolgen als auch bei der Bearbeitung durch unterschiedliche Schülerinnen und Schüler auf und bedarf daher der Thematisierung an dieser Stelle.
Eigenaktivität
Sehen Sie sich die folgenden Schülerlösungen an. Welcher Fehlertyp zeigt sich in all diesen Dokumenten?
Welche Fehlvorstellung der Schülerinnen und Schüler lässt sich daraus ableiten?
Was ist eine mögliche Erklärung?
Wie viele kleine Quadrate hat wohl die 20. Figur?
Zusätzlich zur Rechnung ist jeweils die Tabelle abgebildet, die die Kinder zuvor ausgefüllt hatten und für diese Aufgabe als Grundlage nutzen konnten.
Folge: DREIECKSZAHLEN (Carolin):
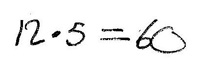
Folge: QUADRATZAHLEN (Felix):

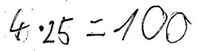
Folge: T-FORM (Carolin):

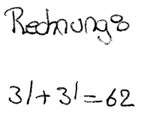
Folge: QUADRATZAHLEN (Leonie):
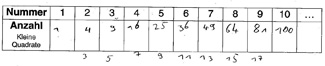
Hier finden Sie die jeweilige Begründung durch den Schüler sowie eine mögliche Erklärung.
Verwandte Themen
Prozessbezogene Kompetenzen
Entdeckendes Lernen
Leistungsstarke Kinder
Material
Interviewleitfaden inklusive Aufgabenblätter
Weitere Informationen zum Thema natürliche Differenzierung und Lernumgebungen:
Krauthausen & Scherer (2010). Umgang mit Heterogenität.
Literatur
© Anne Smirek für das KIRA-Team
