Gerade wenn es um individuelle Förderung im Mathematikunterricht geht, werden die leistungsstarken Kinder bisweilen außen vor gelassen - sie würden den Stoff ja schon beherrschen. Doch bietet man diesen Kindern keine Möglichkeiten, ihre Begabung auszuleben und weiterzuentwickeln, so kann dies schnell zu einer Unterforderung und zu Langeweile im Unterricht führen. Die Kinder verlieren dadurch möglicherweise jede Freude an der Mathematik.
Um auch den mathematisch begabten Kindern gerecht werden zu können, werden Sie auf dieser Seite über mathematische Leistungsstärke und Begabung informiert. Insbesondere die typischen Merkmale von leistungsstarken Kindern im Mathematikunterricht sollen hier näher durchleuchtet werden.
Helena berechnet die 30. Dreieckszahl
Addiert man die Summe aufeinanderfolgender natürlicher Zahlen (1 + 2 + ... +n), so erhält man die sogenannten Dreieckszahlen. Während die Berechnungen der ersten Dreieckszahlen noch leicht durchführbar sind, sind mit den Mitteln der Grundschüler für die Berechnung hoher Dreieckszahlen geschickte Rechenwege notwendig, um nicht "stundenlang" addieren zu müssen. Ein herausforderndes Problem - besonders für die leistungsstarken Kinder im Mathematikunterricht - wie das folgende Beispiel zeigt:

Die Drittklässlerin Helena ermittelt die 30. Dreieckszahl
Helenas Bearbeitung wirkt zwar auf den ersten Blick sehr unübersichtlich, setzt man sich jedoch genauer mit ihrem Lösungsweg auseinander, so wird deutlich, dass sie ein sehr geschicktes und strukturiertes Vorgehen an den Tag gelegt und dabei viel Ausdauer gezeigt hat. Unten links in dem obigen Dokument notierte sie schließlich das richtige Ergebnis: 465.
Es ist zu beachten, dass sich Helena an zwei Stellen verrechnet:
- Sie rechnet: 275 + 39 = 304 (an dieser Stelle hätte sie eigentlich 37 addieren müssen. Die 39 setzt sich aus den zwei Summanden 19 und 20 zusammen. Die 20 wurde allerdings von Helena schon durch die Addition 234 + 41 einbezogen, es wurden also 20 zuviel addiert.
- Da Helena bei der Addition 275 + 39 = 304 um 10 verrechnet (=314) und bei der Rechnung 439 + 15 = 444 (=454) erneut 10 zu wenig addiert, wird die doppelte Addition der 20 ausgeglichen. Helena kommt somit trotzdem zum richtigen Ergebnis.
Wie genau die obige Lösung zustande gekommen ist, können Sie in Abschnitt 4 dieser Seite erfahren - dort finden Sie einen Videoausschnitt aus dem Interview mit Helena.
Hintergrundwissen zu leistungsstarken Kindern
Zunächst muss man sich vor Augen führen, dass ein Kind, das leistungsstark bzw. begabt in Mathematik ist, nicht unbedingt auch in anderen Fächern begabt sein muss. Eine mathematische Begabung ist also nicht mit Hochbegabung im Allgemeinen gleichzusetzen.
Eine mathematische Begabung geht meist mit einigen typischen Merkmalen einher. Dabei unterscheidet man prinzipiell zwischen allgemeinen begabungsstützenden Persönlichkeitseigenschaften und mathematikspezifischen Merkmalen (vgl. Käpnick 1998; Käpnick, Nolte & Walther 2005, S. 13):
Begabungsstützende allgemeine Persönlichkeitseigenschaften
- hohe geistige Aktivität
- intellektuelle Neugier
- Anstrengungsbereitschaft
- Freude am Problemlösen
- Konzentrationsfähigkeit
- Beharrlichkeit
- Selbstständigkeit
- Kooperationsfähigkeit
Mathematikspezifische Merkmale
- Fähigkeit zum Speichern mathematischer Sachverhalte im Kurzzeitgedächtnis unter Nutzung erkannter mathematischer Strukturen
- mathematische Fantasie
- Fähigkeit im Strukturieren mathematischer Sachverhalte
- Fähigkeit im selbstständigen Transfer erkannter Strukturen
- Fähigkeit im selbstständigen Wechseln der Repräsentationsebenen und im selbstständigen Umkehren von Gedankengängen beim Bearbeiten mathematischer Aufgaben
- mathematische Sensibilität
Aufgaben, um (mathematikspezifische) Begabungsmerkmale zu erkennen
Um bei Kindern mathematische Begabung feststellen zu können und um die Kinder im Unterricht herausfordern zu können, ohne den Unterrichtsstoff vorwegzugreifen, bedarf es besondere Aufgaben. Diese sollen das Zurückgreifen auf die o.g. Merkmale ermöglichen und mathematisch gehaltvoll sein. Dabei kann und muss natürlich nicht jede Aufgabe alle Merkmale abdecken.
Im Folgenden möchten wir Ihnen einige Aufgabenbeispiele (vgl. Käpnick 2001) aufzeigen. Ihre Aufgabe ist es, diese zunächst selbst zu lösen.
Eigenaktivität: Zahlen merken
Hier sehen Sie ein 4x4 Feld. Schauen Sie sich das Zahlenfeld 30 Sekunden lang an. Danach schreiben Sie die Zahlen, ohne auf die Vorlage zu gucken, genauso in ein neues, leeres Quadrat.
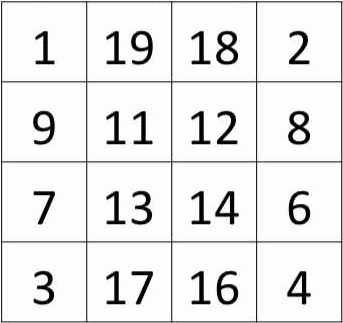
- Wie viele Zahlen konnten Sie sich merken? Wie haben Sie sich diese Zahlen merken können? Hatten Sie eine bestimmte Strategie?
- Konnten Sie Muster in dem Feld erkennen? Wenn nicht, schauen Sie noch einmal genau hin.
- Welche von den oben genannten Merkmalen von Leistungsstärke kann man mit dieser Aufgabe sichtbar machen?
- Welches Vorgehen erwarten Sie von den leistungsstarken Kindern?
Eigenaktivität: Geschickt addieren
Wie groß ist die Summe aller Zahlen der Tabelle aus Aufgabe 1? Wie kann man das Ergebnis möglichst leicht ermitteln?
- Wie haben Sie die Summe berechnet? Fällt Ihnen noch eine andere Strategie ein, die ein geschicktes Ermitteln der Summe ermöglicht?
- Haben Sie bei der Berechnung auf Erkenntnisse aus der ersten Aufgabe zurückgegriffen?
- Welche von den oben genannten Merkmalen von Leistungsstärke kann man mit dieser Aufgabe sichtbar machen?
- Welches Vorgehen erwarten Sie von den leistungsstarken Kindern?
Eigenaktivität: Dreieckszahlen
Hier sehen Sie eine Reihe von Dreiecken. Wie müsste das nächste Dreieck in der Reihe aussehen und aus wie vielen Punkten würde es bestehen?
Wie viele Punkte enthält das Dreieck, das in der untersten Reihe aus 30 Punkten besteht?

- Lösen Sie die Aufgabe auf verschiedenen Wegen.
- Wie könnten die Kinder vorgehen?
- Welche von den oben genannten Merkmalen von Leistungsstärke kann man mit dieser Aufgabe sichtbar machen?
Videoanalyse leistungsstarker Kinder
Im Folgenden können Sie sehen, wie Kinder (Zweit-, Dritt- und Viertklässler) mit den obigen Aufgaben umgehen. Die Kinder wurden jeweils auf Grundlage der Einschätzung ihrer Mathematiklehrerinnen als leistungsstarke Kinder für die Interviews ausgewählt.
Aufgabe 1: Zahlen merken
Helena
Nina
Welche Strategie benutzt das Kind, um sich die Zahlen einzuprägen?
(Versucht es die Zahlen "nur" auswendig zu lernen? Sucht es nach Mustern/Strukturen im Quadrat, die ihm die Reproduktion erleichtern?)
Aufgabe 2: Geschickt addieren
Leon
Helena
Wie bestimmen die Kinder die Summe?
Hätten Sie dieses Vorgehen erwartet?
Welche Begabungsmerkmale zeigen die Kinder?
Aufgabe 3: Dreieckszahlen
Paul
Leon
Helena
Wie sind die Kinder auf die Lösung gekommen?
Hätten Sie dieses Vorgehen erwartet?
Welche Begabungsmerkmale zeigen die Kinder?
Ausblick
Mit der Beachtung dieser Informationen zur Diagnose von Leistungsstärke bzw. mathematischer Begabung haben Sie einen wichtigen Schritt zur individuellen Förderung getan. An dieser Stelle möchten wir Ihnen noch einen kurzen Ausblick zum Umgang mit besonders leistungsstarken Kindern im Unterricht geben.
Damit sich die betroffenen Kinder im Mathematikunterricht nicht unterfordert fühlen, besteht zum einen die Möglichkeit, den Stoff für diese Kinder im Stoff vorzuziehen und ihnen Aufgaben der höheren Schuljahre zu geben. Letztlich verschiebt sich die Problematik der Unterforderung bzw. Langeweile dann aber nur auf den Zeitpunkt, wo eben dieser Stoff zum Unterrichtsthema der ganzen Klasse wird.
Eine andere Möglichkeit der Förderung leistungsstarker Schülerinnen und Schüler ist der Einsatz substantieller Aufgaben, die im Sinne einer natürlichen Differenzierung eine Bearbeitung des Problems durch alle Schülerinnen und Schüler auf ihrem individuellen Niveau zulässt (z.B. Zahlenmauern, Zahlenketten etc.). Sie biten somit auch den leistungsstarken Kindern genügend Anspruch, ohne dass sich diese besonders behandelt fühlen.
Solche Aufgaben bieten den Schülerinnen und Schülern auch die Möglichkeit, selbst Anschlussprobleme zu finden und somit ihre Kreativität und Phantasie anzuregen. Im Zusammenhang mit den Dreieckszahlen könnte man die leistungsstarken Kinder z.B. auffordern, sich selbst ein Punktmuster auszudenken.
Letztlich gilt es vor allem die Fähigkeiten der Kinder zu würdigen und Interesse an ihren Vorgehensweisen zu zeigen, um langfristig ihre Freude an der Mathematik erhalten zu können.
Material
Eine große Auswahl an substanziellen Aufgaben finden Sie z.B. auf folgenden Internetseiten:
Weitere Anregungen liefern z.B. die Bücher von Käpnick, F. (Hrsg.) (2001-2006). Mathe für kleine Asse.
Verwandte Themen
Leistungsschwache Kinder
PIKAS: Heterogenität
primakom: Leistungsstake Kinder
Käpnick, F., Nolte, M. & Walther, G. (2005). Talente entdecken und unterstützen.
Literatur
