IRI-Zahlen

Das Entdecken, Beschreiben und Begründen von Mustern und Strukturen sind die zentralen Tätigkeiten in der Mathematik und auch zentrale Bestandteile des Unterrichts in der Grundschule (vgl. KMK 2005).

Im Rahmen ihrer Bachelorarbeit hat sich Lisa Agethen deshalb mit den verschiedenen Entdeckungen von Kindern zum Thema IRI-Zahlen auseinandergesetzt.

Auf der folgenden Seite werden die wesentlichen Ergebnisse vorgestellt und anhand von Schülerdokumenten illustriert, die im Rahmen der Arbeit entstanden sind.

Ein Beispiel zum Einstieg

Bevor es um die Berechnung von Aufgaben und um die Entdeckungen in den Ergebnissen ging, sollten die Kinder verschriftlichen, warum die gegebenen Beispielzahlen IRI-Zahlen heißen.

Beispielzahlen: 575, 343, 919, 585, 424, 131, 272

Dabei fielen besonders die Antworten von Marc und Celina auf:

Eigenaktivität

Schauen sie sich die Antworten der beiden Schüler an und überlegen Sie, wie Sie mit den Antworten der Kinder im Unterricht umgehen würden.

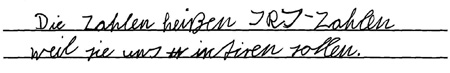
Schülerdokument von Mark: „Die Zahlen heißen IRI-Zahlen, weil sie uns irritieren sollen.“ (Rechtschreibung angepasst)
Marcs Antwort

Schülerdokument von Celina: „Weil zum Beispiel bei 343 die erste und die dritte Zahl gleich sind und bei dem Wort IRI ist es genau so nur halt mit Buchstaben.“ (Rechtschreibung angepasst)
Celinas Antwort

 

Eigenaktivität

Bevor Sie sich nun das Hintergrundwissen zu den IRI-Zahlen durchlesen, versuchen Sie doch zunächst selbst, die IRI-Zahlen zu erforschen.

  1. Wie viele verschiedene IRI-Zahlen gibt es? Warum sind Sie sich sicher, dass Sie alle gefunden haben?
  2. Aus zwei Ziffern lassen sich zwei verschiedene IRI-Zahlen bilden.

Beispiel:

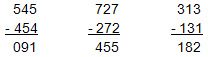
Beispielaufgaben in schriftlicher Subtraktion: „545 minus 454 = 091“, „727 minus 272 = 455“, „313 minus 131 = 182“.

Wenn Sie weitere solcher IRI-Aufgaben rechnen, werden Sie verschiedene Muster in den Aufgaben und den Ergebnissen entdecken.

Welche Muster entdecken Sie? Können Sie diese Muster auch erklären?

Hintergrundwissen: IRI-Zahlen

Das Aufgabenformat

Das Aufgabenformat der IRI-Zahlen ist eine Variation der ANNA-Zahlen (vgl. Verboom 1998) und dient dem strukturierten Üben der schriftlichen Subtraktion. Das Berechnen der Aufgaben festigt das Ausführen des schriftlichen Subtraktionsalgorithmus und bietet gleichzeitig die Möglichkeit, Muster und Zusammenhänge zu entdecken, zu beschreiben und zu begründen.

Die IRI-Zahlen sind so aufgebaut, dass jeweils die Hunderter- und Einerziffer identisch sind (zum Beispiel 727 oder 131). Es dürfen bei der Bildung der Zahlen alle Ziffern von 0-9 gewählt werden. Aus zwei Ziffern lassen sich zwei verschiedene IRI-Zahlen bilden. Subtrahiert man jeweils die kleinere von der größeren IRI-Zahl, entstehen IRI-Aufgaben.
Beispiele für IRI-Aufgaben:

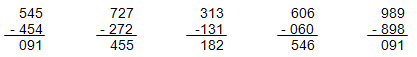
Beispielaufgaben für IRI-Aufgaben mit dem schriftlichen Subtraktionsalgorithmus: „545 minus 454 = 091, 727 minus 272 = 455, 313 minus 131 = 182, 606 minus 060 = 546, 989 minus 898 = 091“.

Insgesamt gibt es 45 verschiedene Aufgaben und als Ergebnisse einer IRI-Aufgabe erhält man immer Vielfache von 91, nämlich: 91, 182, 273, 364, 455, 546, 637, 728 und 819.

Welches Vielfache von 91 die Ergebniszahl bildet, ist abhängig von der Differenz der Ziffern. Wenn die Zifferndifferenz zum Beispiel 3 beträgt, dann lässt sich das Ergebnis der entsprechenden Aufgabe auch durch die Aufgabe 3*91 berechnen.

Eigenaktivität

Überlegen Sie, warum die Ergebnisse Vielfache von 91 sind und warum die Ergebnisse von der Zifferndifferenz abhängig sind.

Wie würden Sie diesen Zusammenhang Schülern anschaulich erklären?

Hier finden Sie Vorschläge zur Erklärung des Zusammenhangs: IRI-Zahlen: Erklärung

Entdeckungen

Bezüglich der Ergebnisse von IRI-Aufgaben lassen sich verschiedene Entdeckungen machen, die von den Schülern nicht nur beschrieben, sondern zum Teil auch begründet werden können. Dies zeigt, dass sich das Aufgabenformat zur natürlichen Differenzierung eignet, da jedes Kind auf seinem eigenen Leistungsniveau arbeiten kann.

Dabei werden einige Kinder ihre Entdeckungen nur beschreiben, wohingegen andere Kinder schon fähig sind, die gefundenen Gesetzmäßigkeiten zu begründen. Unabhängig vom Leistungsniveau jedoch ist es immer möglich, prozessbezogene Kompetenzen anzusprechen und weiterzuentwickeln.

Mögliche Entdeckungen, die von den Kindern gemacht werden können, sind:

  • Die Quersumme der Ergebnisse steigt von Ergebnis zu Ergebnis um eins an, beginnend bei zehn.
  • Die Hunderter- und Zehnerstelle der Ergebnisse ergeben jeweils als Zahl gelesen ein Vielfaches von neun.
  • Die Einerstelle des Ergebnisses liefert den Faktor, mit dem man 91 multiplizieren muss, um dieses Vielfache zu erhalten.
  • Die Hunderter- und Einerstelle der Ergebnisse werden jeweils um eins größer und die Zehnerstelle um eins kleiner.
  • Die Differenz zwischen den gewählten Ziffern gibt den Faktor an, mit dem man 91 multiplizieren muss, um das Ergebnis der IRI-Aufgaben zu erhalten.
  • Die Summe aus Hunderter- und Zehnerziffer der Ergebnisse ergibt jeweils neun.
  • Die Summe aus Zehner- und Einerziffer der Ergebnisse ergibt jeweils zehn.

Erklärungsstrategien

Bei allen Erklärungen der Kinder kann zwischen zwei verschiedenen Vorgehensweisen unterschieden werden. Einige Kinder erklären ihre Entdeckungen anhand von Beispielen, wohingegen andere Kinder ihre Entdeckungen verallgemeinern.

Im Folgenden werden die Antworten der Kinder zur Fragestellung „Warum heißen die Zahlen IRI-Zahlen?" exemplarisch vorgestellt, um daran die beiden Vorgehensweisen zu verdeutlichen.
 

beispielgebundene Erklärungen:

Schülerdokument: „IRI 575“.
("IRI 575")

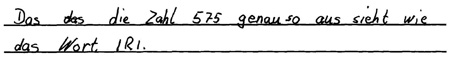
Schülerdokument: „Das die Zahl 575 genauso aussieht wie das Wort IRI.“
("Das die Zahl 575 genauso aus sieht wie das Wort IRI.")

 

Schülerdokument: „Weil zum Beispiel bei 343 die erste und die dritte Zahl gleich sind und bei dem Wort IRI ist es genau so nur halt mit Buchstaben.“
("Weil: z.b. bei 343 die erste und die dritte Zahl gleich sind und bei den Wort IRI ist es genau so nur halt mit Buchstaben")

allgemeine Erklärungen:

Schülerdokument: „Weil die Zahlen immer zwei Zahlen gleich sind.“
("Weil die Zahlen immer zwei Zahlen gleich sind")

Schülerdokument „Bei dem Wort IRI ist vorne das I und hinten auch. Bei den Zahlen ist das das gleiche.“
("Bei dem Wort IRI ist vorne das I und hinten auch. Bei den Zahlen ist das das gleiche.")

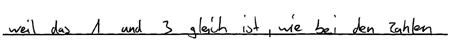
Schülerdokument: „Weil das 1 und 3 gleich ist, wie bei den Zahlen.“
("Weil das 1 und 3 gleich ist, wie bei den Zahlen")

Bei den exemplarischen Schülerantworten fallen nicht nur die beiden unterschiedlichen Erklärungsstrategien auf, sondern auch, dass es nicht immer ganz leicht ist, die Antworten zu verstehen.

Als Grund dafür lässt sich zum einen nennen, dass es einigen Schülern schwer fällt, ihre Entdeckungen in Worte zu fassen und zum anderen, dass die Kinder manchmal ganz anders denken als wir selbst. Deshalb ist es hilfreich, die Schüler ihre Antworten auch mündlich erklären zu lassen, um ihre Denkweisen zu verstehen.

Eigenaktivität

Lesen Sie sich die Antwort von Maximilian genau durch und überlegen sie, was Maximilian gemeint haben könnte.

Abbildung der Zahlen „575, 343, 919, 585, 424, 131, 272“. Darunter: „Warum heißen die Zahlen IRI-Zahlen?“ Schülerlösung: „Diese Zahlen heißen IRI-Zahlen, weil sie einen irritieren. Die Zahlen sind vorne und hinten gleich zum Beispiel 575 und manchmal ist die Zahl in der Mitte wenn man zur ersten Zahl noch zwei dazu tut, die Zahl rauskommt.“

Hier finden Sie Maximilians Erklärung zu seiner Entdeckung:

IRI-Zahlen: Maximilian erklärt

Kinder als Entdecker

Wenn es darum geht, dass die Kinder Entdeckungen bezüglich der IRI-Aufgaben machen, dann wird deutlich, dass alle Kinder etwas entdecken können. Dies spricht dafür, dass die IRI-Zahlen ein substantielles Aufgabenformat sind, an dem alle Kinder auf ihrem Niveau arbeiten können.

Dabei machen einige Kinder mehr Entdeckungen als andere. Grundsätzlich haben alle Kinder entdeckt, dass einige Ergebnisse mehrfach vorkommen. Im Folgenden zeigen die Dokumente die weiteren Entdeckungen der Kinder.

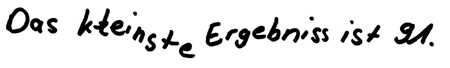
Schülerdokumente: „Das kleinste Ergebnis ist 91. Wenn die Ergebnisse gleich sind, ist es immer derselbe Abstand bei den Aufgaben. Die Ergebnisse werden um 91 größer. Das bei den Hundertern Ergebnissen immer der Einer größer ist als der Hunderter. Die Ergebnisse sind vorne und hinten nicht doppelt. Wenn der Ziffernunterschied gleich ist kommt das gleiche Ergebnis raus. Wenn der Unterschied 5 ist kommt 455 raus. Wenn der Unterschied 4 ist kommt 364 raus. Wenn der Unterschied 2 ist kommt 182 raus. Wenn der Unterschied 3 ist kommt 273 raus. Wenn der Unterschied 1 ist kommt 91 raus. Die Quersumme wird immer 1 größer die kleinste ist 10. Die Hunderter und einer beim Ergebnis sind aus der Neunerreihe. Der Zehner und Einer sind zusammen immer 10.“

 

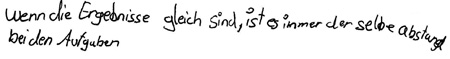
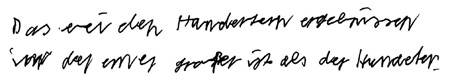
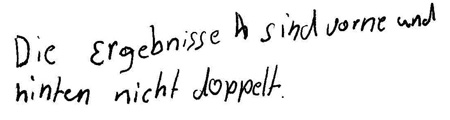
Verwandte Themen

Prozessbezogene Kompetenzen
Reihenfolgezahlen
Schöne Päckchen
Zahlengitter
Triff die 50
schriftliche Subtraktion

PIKAS: Gute Aufgaben (u. a. zu "Umkehrzahlen")

Weitere Informationen zum produktiven Üben mit verschiedenen Zahlenmustern finden Sie in Produktives Üben mit ANNA-Zahlen und anderen Zahlenmustern (Verboom 1998, S. 48f.)

Material

Interviewleitfaden mit Arbeitsblättern

Literatur

© Lisa Agethen für das KIRA-Team 

Kurz-URL: https://kira.dzlm.de/node/140

QR-Code downloaden