„Was fällt dir auf?" und „Warum ist das so? Begründe!" sind Aufgabenstellungen, die Kinder zum Entdecken, Beschreiben und Begründen von Mustern und Strukturen anregen und dadurch prozessbezogene Kompetenzen wie das Argumentieren fördern sollen.
Auch Kinder aus den unteren Jahrgangsstufen sind dazu bereits in der Lage. Wie unterschiedlich sie mit diesen Anforderungen umgehen, wollen wir Ihnen auf dieser Seite am Beispiel des Aufgabenformats „Schöne Päckchen" (vgl. Wittmann & Müller 2004) aufzeigen.
"Wenn klein und groß sich verbinden, dann sind das immer 10"
Laut den Bildungsstandards und dem Lehrplan des Landes NRW sollen die Kinder bis zum Ende von Klasse 4 lernen, „Vermutungen über mathematische Sachverhalte (Gesetzmäßigkeiten, Beziehungen, Ausnahmen) aufzustellen und anhand von repräsentativen Beispielen oder von allgemeinen Überlegungen zu bestätigen oder zu widerlegen" (Selter 2004, S. 23).
Eigenaktivität
Im folgenden Video sehen Sie, wie der Zweitklässler Önder ein sogenanntes schönes Päckchen bearbeitet.
Welche der oben genannten Teilkompetenzen zeigt er dabei bereits?
Önder
Prozessbezogene Kompetenzen im Kontext von schönen Päckchen
Wie Sie auf der Seite „Prozessbezogene Kompetenzen - eine Einführung" nachlesen können, unterscheidet man im Mathematikunterricht zwischen inhaltsbezogenen und prozessbezogenen Kompetenzen.
Während bei klassischen Rechenpäckchen (von Wittmann 1994 auch als „Graue Päckchen" bezeichnet) nur das reine Ausrechnen geübt wird, bieten die sogenannten schönen Päckchen (vgl. Wittmann & Müller 2004) bereits in den unteren Jahrgangsstufen die Möglichkeit, sich mit Zahlbeziehungen und mathematischen Gesetzmäßigkeiten auseinanderzusetzen, sodass sowohl inhalts- als auch prozessbezogene Kompetenzen auf vielfache Weise angesprochen werden.
Unter schönen Päckchen versteht man eine Serie von Aufgaben, die nicht willkürlich zu einem Rechenpäckchen zusammengefasst worden sind, sondern die in einem bestimmten Zusammenhang stehen, indem sie sich etwa von Aufgabe zu Aufgabe operativ verändern. Das dadurch entstehende Muster muss dabei noch nicht einmal sonderlich kompliziert sein, wie auch das folgende Beispiel zeigt:
Graues Päckchen
6 + 1 = 7
8 + 3 = 11
2 + 7 = 9
9 + 5 = 14
4 + 4 = 8
Schönes Päckchen
5 + 5 = 10
6 + 4 = 10
7 + 3 = 10
8 + 2 = 10
9 + 1 = 10
So lassen sich an diesem schönen Päckchen beispielsweise folgende Muster bzw. operative Veränderungen entdecken:
- Der 1. Summand wird von Aufgabe zu Aufgabe immer um eins größer.
- Der 2. Summand wird von Aufgabe zu Aufgabe immer um eins kleiner.
- Das Ergebnis bleibt bei allen Aufgaben gleich.
Schöne Päckchen regen die Kinder somit zum Entdecken und zum Erforschen (einfacher) mathematischer Zusammenhänge an, für die die Kinder anschließend Vermutungen und erste Begründungen entwickeln.
Die bei schönen Päckchen entstehenden Muster der Ergebnisse bieten zudem eine gute Möglichkeit der Selbstkontrolle. Denn die Kontrolle erfolgt hier nicht von außen (z.B. durch die Lehrerin oder extra Lösungskärtchen), sondern unmittelbar „aus der Sache heraus". Im obigen Beispiel erkennen die Kinder schnell, wenn ein Ergebnis nicht in das Muster „immer 10" passt. Das Rechnen wird beim Lösen des Päckchens ganz automatisch geschult.
Dem Erkennen und Nutzen von Mustern und Strukturen kommt eine wesentliche Rolle im Mathematikunterricht zu. Muster und Strukturen bestimmen häufig die einzelnen Themenbereiche und können zur Verdeutlichung zentraler mathematischer Grundideen genutzt werden. Von daher werden sie [...] nicht als eigener Bereich ausgewiesen, sondern sind integraler Bestandteil aller Bereiche.
MSW NRW 2008, S. 56
Wie das obige Zitat aus dem Lehrplan zeigt, kann das Erkennen und Nutzen von Strukturen bei schönen Päckchen unterschiedlichen Bereichen des Lehrplans zugeordnet werden. Im Folgenden möchten wir dies vordergründig mit dem Fokus auf prozessbezogene Kompetenzen betrachten.
In Hinblick auf den Arbeitsauftrag im obigen Video („Was fällt dir auf?") werden insbesondere Teilaspekte der prozessbezogenen Kompetenz des Argumentierens angesprochen, denn das Kind wird durch diese Aufgabenstellung angeregt, mathematische Zusammenhänge oder Auffälligkeiten innerhalb des schönen Päckchens zu entdecken und erste Vermutungen darüber anzustellen (vgl. MSW NRW 2008, S. 60).
So fällt Önder im Einstiegsbeispiel zunächst auf, dass sich die Summanden von Aufgabe zu Aufgabe jeweils um 1 vergrößern bzw. verkleinern, und er beschreibt dies im Rahmen seiner sprachlichen Mittel:
„Das (zeigt von oben nach unten auf die ersten Summanden) ist immer 1 mehr und das (zeigt von oben nach unten auf die zweiten Summanden) ist immer 1 weniger."
Des Weiteren können die Kinder bei diesem Aufgabenformat durch Fragestellungen wie z.B. „Warum ist das so? Begründe!" dazu angeregt werden, die in schönen Päckchen enthaltenen Beziehungen und Gesetzmäßigkeiten an Beispielen zu begründen (vgl. ebd.).
Önders Aussage „Wenn klein und groß sich verbinden, dann sind das immer 10" zeigt, dass er nun versucht, seine vorher entdeckten Beziehungen auch zu begründen. Dies macht er an dem konkreten Beispiel dieses speziellen schönen Päckchens fest. Ob er daraus eine allgemeine Überlegung entwickeln könnte („Immer wenn ..., dann ..."), darüber lässt sich hier keine Aussage tätigen.
Denn um diesen Aspekt des Argumentierens (folgern) anzuregen, wäre es notwendig, ihn weitere analoge Päckchen untersuchen zu lassen und ihn ggf. explizit zu fragen „Ist das immer so? Warum?".
Önders Äußerungen lassen sich bereits, zumindest aus Erwachsenensicht, gut nachvollziehen. Deiktische Ausdrücke wie „Das" und das gleichzeitige Zeigen auf die Stelle, die Önder meint, sind jedoch noch ungenau und würden etwa bei der Bearbeitung schriftlicher Aufgaben nicht eindeutig sein.
Es gilt daher, im Sinne der prozessbezogenen Kompetenz des Darstellens und Kommunizierens, ihn auf lange Sicht dazu anzuregen, mathematische Fachbegriffe und Konventionen zu verwenden (vgl. MSW NRW 2008, S. 60). Dies ist trotz aller Individualität wichtig, um eine gemeinsame Sprache im Mathematikunterricht zu etablieren und Missverständnisse zu vermeiden.
Wie sich Beschreibungen von Kindern sprachlich unterscheiden können, hat Link (2007) am Beispiel von schriftlichen Dokumenten zu schönen Päckchen bzw. Entdeckerpäckchen untersucht.
In der folgenden Abbildung (Link 2007) sehen Sie die Antworten einiger Drittklässler zu der Frage „Was fällt dir auf?".
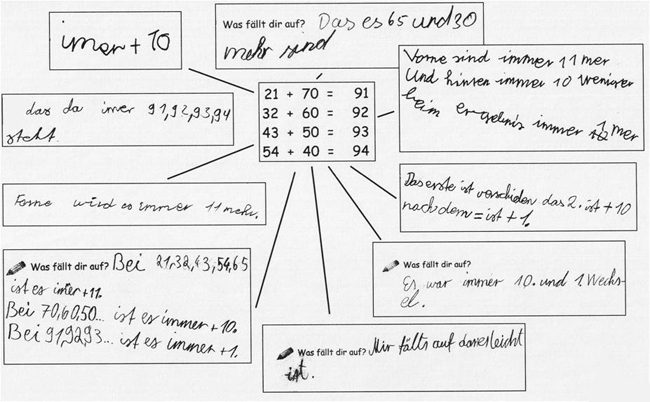
Eigenaktivität
Was fällt Ihnen an den Schülerdokumenten auf?
- Welche Kompetenzen sehen Sie in den einzelnen Antworten der Kinder?
- Welche Verbesserungsmöglichkeiten sehen Sie in einzelnen Antworten?
- Welche Gemeinsamkeiten und Unterschiede gibt es?
Hier finden Sie einige Ergebnisse von Link (2007) zu einer möglichen Kategorisierung der obigen Antworten:
Schöne Päckchen: Beispiele Link
Die Ergebnisse von Link (2007) zeigen auf, dass sich eine mathematische Fachsprache nicht von selbst und auch nicht von heute auf morgen entwickelt. Vielmehr muss sie von Beginn an und über die gesamte Schulzeit angebahnt und gefördert werden.
Videoanalyse
Während Sie in den Dokumenten von Link (2007) schriftliche Äußerungen von Drittklässlern betrachten konnten, können Sie sich nun mit mündlichen Beschreibungen sowie Begründungen von Zweitklässlern auseinandersetzen.
Dazu haben wir den Kindern im Interview folgendes schönes Päckchen vorgelegt:
2 + 6 =
3 + 6 =
4 + 6 =
5 + 6 =
__+ __=
__+ __=
Eigenaktivität
Betrachten Sie die Videos unter folgenden Aspekten:
- Welche Auffälligkeiten beschreiben die Kinder?
- Inwiefern gelingt es ihnen, diese Auffälligkeiten auch zu begründen und sich dabei von der „beschreibenden Ebene" zu lösen?
- Wie formulieren die Kinder ihre Entdeckungen?
- Ziehen Sie dazu die Kategorien von Link heran.
- Inwiefern sehen Sie Unterschiede zwischen den mündlichen Beschreibungen und Begründungen der Kinder in den Interviews und den obigen schriftlichen Antworten?
Önder
Carla
Nils
Daniel
Weiterführende Aufgaben
Schöne Päckchen als Eigenproduktion
Wenn die Kinder das Grundprinzip der schönen Päckchen verstanden haben, kann die Aufgabenstellung auch lauten „Erfinde ein eigenes schönes Päckchen". Denn wenn Kinder zu dieser Art von Eigenproduktionen angeregt werden, wird zusätzlich die prozessbezogene Kompetenz des Problemlösens/Kreativseins angesprochen, da nun die Kinder ermutigt werden, eigene Aufgaben zu erfinden und das Wissen über die Strukturhaltigkeit schöner Päckchen auf ein eigenes zu übertragen (vgl. MSW NRW 2008, S. 59).
Die Kinder können dadurch auf ihrem jeweiligen Niveau zeigen, was sie können und die Lehrperson erhält zusätzliche, oftmals sehr aufschlussreiche und interessante Informationen über das Kind.
Mögliche Beobachtungshilfen könnten bspw. sein:
- Welche Zahlenwerte wählt das Kind? (Zahlenraum, Aufgaben mit/ohne Zehnerübergang o.ä. Herausforderungen)
- Welche Rechenoperation wählt das Kind?
- Welche Art von Muster wählt das Kind? (z.B. einfaches oder anspruchsvolleres Muster, durchgängiges Konstruktionsprinzip, ...)
- Wie geht das Kind bei der Konstruktion des Musters vor?
- Inwiefern kann das Kind sein eigenes Päckchen lösen?
- Inwiefern nutzt das Kind sein eigenes Muster aus, um die einzelnen Ergebnisse zu bestimmen?
- Inwiefern kann das Kind das Muster in dem eigenen Päckchen erklären?
- ...
Bei all diesen Beobachtungen ist ein kompetenzorientierter Blick unumgänglich:
Um die Leistungen der Kinder zu würdigen, sollte die Lehrperson erst einmal in den Blick nehmen, was die Kinder schon können und welche individuellen Stärken sie zeigen, bevor die Schwierigkeiten der Kinder betrachtet werden.
Die Schwierigkeiten sollen auch hier natürlich nicht ignoriert, aber auch nicht übergeneralisiert werden: nur weil ein Kind ein einfaches Muster wählt, heißt es nicht automatisch, dass es nicht in der Lage ist, ein schwierigeres Muster zu erfinden. Es zeigt erst einmal nur, dass sich das Kind mit dem einfachen Muster sicher zu fühlen scheint.
Eigenaktivität
Im Folgenden sehen Sie drei Kinder, die ihr jeweils eigenes schönes Päckchen erfinden.
Welche individuellen Besonderheiten lassen sich durch die Eigenproduktion bei jedem Kind ausmachen? Die o.g. Beobachtungshilfen können Ihnen dabei Orientierung geben.
Daniel
Önder
Janina
Mögliche Interpretationen zu den drei Eigenproduktionen finden Sie hier:
Schöne Päckchen: Interpretation Eigenproduktionen
Schöne Päckchen zur Selbstkontrolle
Im Hintergrundwissen wurde bereits kurz angedeutet, dass sich schöne Päckchen besonders gut zur Selbstkontrolle „aus der Sache heraus" eignen. Wie Kinder dies nutzen, d.h. ihre Rechnungen selbst noch einmal überprüfen und verbessern, können Sie hier bei Carla und Önder sehen. Beide bearbeiten das schöne Päckchen 5-5, 6-4, 7-3, 8-2, usw.
Carla
Carla hat zuvor das schöne Päckchen 5+5, 6+4, 7+3, 8+2, usw. bearbeitet. Sie erkennt, dass das Päckchen 5-5, 6-4, 7-3, 8-2 fast das gleiche Päckchen wie vorher ist, nur jetzt minus anstatt plus gerechnet werden soll.
Bei der Frage der Interviewerin, was Carla als Ergebnisse bei dem Minuspäckchen erwarte, überträgt sie ihre zuvor gemachten Entdeckungen des Pluspäckchens „Ergebnis immer gleich 10" auf das Minuspäckchen und äußert als Vermutung, dass das Ergebnis immer „0" sein müsste. Ohne zu rechnen schreibt sie „0" dann auch bei den Aufgaben als Ergebnis hin.
Erst als sie das Päckchen weiter führt und 10-0 rechnen will, bemerkt sie ihren Denkfehler und verbessert die Ergebnisse. Dabei schleicht sich ein Rechenfehler ein. Diesen Fehler entdeckt sie allerdings durch die Beobachtung, dass das Ergebnis immer um zwei größer wird.
Önder
Önder macht beim Lösen der Aufgabe 7-3=5 einen Rechenfehler. Als er dann das Päckchen weiterführt, bemerkt er, dass die Ergebnisse keine direkte „Reihenfolge" bilden (wie z.B. 8, 9, 10, 11, 12), sondern die Ergebnisse in Zweierschritten größer werden: „0, 2, 4, 6, 8, 10". Sein Ergebnis 7-3=5 stört jedoch dieses Muster.
Er kontrolliert seine Rechnung noch einmal und verbessert das Ergebnis, sodass es nun ein ‚echtes' schönes Päckchen wird. In seiner Beobachtung, wie sich die Minuenden („das geht so hoch") und die Subtrahenden („und das geht von hoch zu tief") verändern, liegt zudem bereits ein Versuch einer Begründung dafür, warum das Ergebnis genau um zwei größer wird.
Verwandte Themen
Kompetenzen im Mathematikunterricht
Zahlengitter
Reihenfolgezahlen
PIKAS: Entdecken, Beschreiben, Begründen (u. a. ahnand schöner Päckchen)
PIKAS: Sprachbildung
PIKAS: Sprachförderung im Mathematikunterricht
PIKAS: Gute Aufgaben
Material
Interviewleitfaden
Literatur
