Die Null ist eine besondere Zahl. Ob geschichtlich betrachtet, im alltäglichen Sprachgebrauch oder beim Rechnen: Sie unterscheidet sich von den anderen Zahlen und stellt deshalb Kinder im Mathematikunterricht immer wieder vor Herausforderungen. Was genau die Null so besonders macht und wie die Kinder mit diesen Besonderheiten umgehen, erfahren Sie auf dieser Seite.
„Beim Rechnen ist es nichts, ..."
Im Folgenden sehen Sie einen Interviewausschnitt, in dem wir zwei Kinder am Ende des 1. Schuljahres zu ihrem Verständnis der Zahl Null befragt haben.
Eigenaktivität
Bevor Sie sich das Video anschauen, überlegen Sie, wie Sie einem Kindergartenkind erklären würden, was die Null bedeutet.
Hintergrundwissen zur Besonderheit der Null
Die Null im Alltag
In unserem Alltag begegnet uns die Null in vielerlei Hinsicht: Die Doppelnull „00" steht als Hinweis für „das stille Örtchen", die Zahlenfolge „007" assoziieren wir mit einem Superagenten, die Null in Redewendungen steht beispielsweise für einen Neuanfang („Wir fangen noch mal bei Null an.") oder auch als Ausdruck der Geringschätzung („Du bist `ne Null").
Zeigt uns ein Thermometer 0° C an, wissen wir, dass die Straßen glatt werden könnten, und dass wir uns besser warm anziehen. Doch was genau bedeutet die Null aus mathematischer Sicht und somit für den Mathematikunterricht? Erste Aufschlüsse darüber gibt ein Blick auf die Geschichte der Null.
Zur Geschichte der Null
Die Null lässt sich nicht auf einen „einzigen Erfinder" zurückführen. Vielmehr lassen sich in den verschiedenen Hochkulturen unterschiedliche Entwicklungen ausmachen. Lange Zeit kam man ohne das Zahlsymbol „0" aus, erst durch die Einführung von Stellenwertsystemen wurde es notwendig.
Anfangs wurden nicht besetzte Stellen zunächst einfach leer gelassen. So wurde um die Zeit 2000 v. Chr. beispielsweise die 308 noch wie folgt geschrieben: 3 8. Für die Betrachter stellte sich dadurch aber immer die Frage, ob die Lücke zwischen den Zahlen beabsichtigt, oder ob der Abstand zwischen zwei Ziffern nur etwas groß geraten ist (vgl. Volkert 1996, S. 100).
Um dieses Problem zu lösen und um auch fehlende Einheiten eindeutig bezeichnen zu können, wurden nach und nach Symbole für die bis dahin leeren Stellen entwickelt, die in den verschiedenen Kulturen höchst unterschiedlich waren - erste Vorgänger unseres heutigen Zahlsymbols „0" waren somit entstanden.
Gemeinsam war ihnen, dass diese Zahlsymbole (Ziffern) für die Null erst einmal nur eine Platzhalter-Funktion hatten. Vermutlich erst später entwickelte sich eine Vorstellung von der Null als Zahlenwert (eine Menge mit null Elementen; „nichts") (vgl. Ifrah 1991). Wann genau sich dieser „Sprung" von der Null als Platzhalter (Ziffer) hin zu der Vorstellung der Null als Zahl vollzog, ist bislang nicht bekannt.
Folgende Abbildung (entnommen aus: Ifrah 1991, S. 483) gibt einen Überblick über die verschiedenen Symbole und die Entwicklung der Null in den verschiedenen Kulturen:
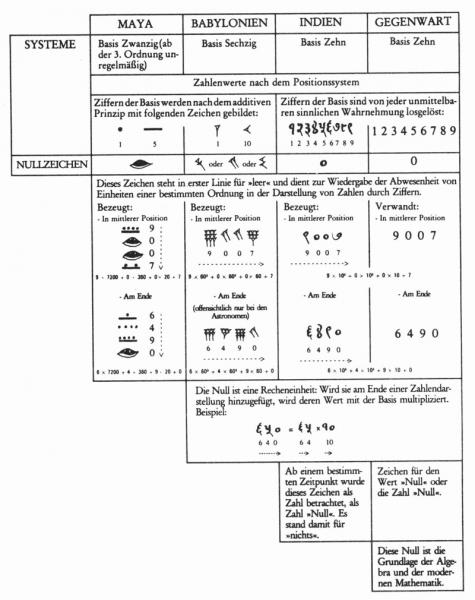
Vergleich der verschiedenen Nullen der Geschichte
Inwiefern sich die Entwicklungen der Null in den verschiedenen Kulturen gegenseitig bedingt haben, oder ob sie unabhängig voneinander zu sehen sind, darüber gibt es bisweilen keine sicheren Quellen (vgl. Ifrah 1991, S. 503).
Bedeutung der Null
Wie sich schon in der Geschichte der Null gezeigt hat, muss man zwischen der Null als Ziffer und der Null als Zahl unterscheiden. Die Null als Ziffer hat ihre Bedeutung vor allem im Hinblick auf Zahldarstellungen. Erst die Erfindung der Null als Ziffer hat es möglich gemacht, mit nur zehn Symbolen sämtliche Zahlen eindeutig darzustellen und ist somit unverzichtbar.
Welche Bedeutung die Null insbesondere als Zahl hat, wird deutlich, wenn man die Null aus der Perspektive der verschiedenen Zahlaspekte betrachtet. In diesem Zusammenhang zeigt sich auch, dass es im Vergleich zu anderen Zahlen einige Besonderheiten gibt:
- Die Frage „Wie viele?" (Kardinalzahlaspekt) wird durch Anzahlen beantwortet. Für die Null gilt dabei die Besonderheit, dass sie jedoch nicht das Produkt einer Zählhandlung ist, sondern Ausdruck dessen, dass „nichts" zum Zählen da ist. Diese Eigenschaft unterscheidet die Null von den anderen endlichen Zahlen (vgl. Hefendehl-Hebeker 1981, S. 241 ff.). Darüber hinaus wird die Null im täglichen Sprachgebrauch oft durch Synonyme ersetzt, die sprachlich gesehen natürlicher erscheinen. Zum Beispiel wird die Frage „Wie viele Äpfel haben wir noch?" nicht mit „0 Äpfel" beantwortet, sondern mit „keine Äpfel".
- Für den Operatoraspekt („Wie oft?") gilt entsprechendes. Die Frage beispielsweise, wie oft Sie dieses Jahr schon den Mount Everest bestiegen haben, werden Sie vermutlich mit „gar nicht" beantworten und nicht mit dem mathematischen Ausdruck „0 mal" (vgl. ebd.).
- Die Null findet natürlicherweise keine ordinale Verwendung (Ordinalzahlaspekt). Im Sprachgebrauch finden sich dennoch Ausdrücke wie „nullte Stunde", „nullte Stufe", „nulltes Kapitel". Hiermit soll meist etwas (einer eigentlich betrachteten Rangfolge) Vorangestelltes bezeichnet werden (vgl. ebd.).
- Im Maßzahlaspekt verwendete Zahlen beziehen sich auf Größen. Ein leeres Konto wird beispielsweise mit dem Betrag 0,00 € verbucht. Fragen wie „Wie lang?" oder „Wie teuer?" werden mit Hilfe von Zahlen in Kombination mit einer geeigneten Maßeinheit beantwortet. Im alltäglichen Sprachgebrauch jedoch finden sich auch hier Synonyme wie „kostenlos" oder „gratis" für den Ausdruck, dass 0 € gezahlt werden müssen (vgl. ebd.).
- Der Codierungsaspekt ist der einzige Zahlaspekt, in dem der Null keine besondere Rolle zukommt. So hat sie beispielsweise in Telefonnummern oder Hausnummern eine gleichwertige Bedeutung wie jede andere Zahl auch (vgl. ebd.).
- Mit der Null kann auch gerechnet werden (Rechenzahlaspekt). Welche Besonderheiten, aber auch Stolpersteine dies mit sich bringt, wird im nächsten Abschnitt erläutert.
Insgesamt zeigt sich, dass wir im alltäglichen Sprachgebrauch auch ohne die Null als Zahl(-wort) auskommen, was zur Folge haben kann, dass man die Null zwar als Ziffer, aber nicht zwingend als Zahl sieht. Eine Problematik, die sich nicht nur in der Geschichte der Null, sondern auch beim Lernen von Mathematik widerspiegelt.
Rechnen mit der Null
Beim Rechnen nimmt die Null insofern eine besondere Rolle ein, als dass für sie besondere Rechenregeln gelten:
Denn jede Addition einer beliebigen Zahl x mit Null ergibt stets wieder x, jede Multiplikation einer beliebigen Zahl x mit Null immer Null und eine Division durch Null ist gar nicht möglich - somit unterscheidet sich die Null wesentlich von allen anderen Zahlen.
Umgang der Kinder mit der Null
Kinder erklären die Null
Im Einstiegsbeispiel haben Sie bereits einen ersten Eindruck davon gewonnen, welche Vorstellungen Kinder von der Null haben. So erklärt Michele im obigen Video: „Beim Rechnen ist es nichts, aber wenn man es schreibt, sieht es so aus (zeigt auf das Zahlsymbol 0)". Sie unterscheidet hier also ganz konkret zwischen dem Zahlsymbol und der Rechenzahl 0. Eine Bedeutung hat die Null für sie jedoch nur als Zahlsymbol („Dann ist die Null eine richtige Zahl").
Im Folgenden sehen Sie ein Video, in dem weitere Kinder ihre Vorstellungen zur Null erläutern.
Eigenaktivität
Welche Eigenschaften der Null finden Sie in den Erläuterungen der Kinder wieder?
Kinder rechnen mit der Null
Im Folgenden können Sie sich anschauen, wie Kinder bei verschiedenen Rechenoperationen mit der Null umgehen und welche Schwierigkeiten und/oder Fehlvorstellungen sie dabei (noch) haben.
Die Interviews orientieren sich an den Erkundungsaufgaben zum „Rechnen mit der Null" von Selter und Spiegel (1997, S. 138 f.). Dort finden Sie auch eine Begründung der Aufgabenauswahl.
Eigenaktivität
Stellen Sie heraus, was die einzelnen Kinder schon über die Besonderheiten der Null beim Rechnen wissen und welche Schwierigkeiten sie gegebenenfalls noch haben.
Michele und Nina (1. Sj.)
Anna-Lisa (2. Sj.)
Anja (4. Sj.), Teil 1
Anja (4. Sj.), Teil 2
Mathias (4. Sj.)
Lars (4. Sj.)
Hier finden Sie Interpretationsvorschläge zu den einzelnen Videos in Hinblick auf die obige Fragestellung:
Michele und Nina Anna-Lisa Anja (Teil 1 und 2) Mathias Lars
Konsequenzen für den Unterricht
Wie die obige Videoanalyse aufgezeigt hat, kommt es häufig bei den Kindern beim Rechnen mit der Null unter anderem zu Verallgemeinerungen der Art, dass die Null entweder fortwährend als neutral betrachtet wird („Die Null ist nichts und hat somit keine Auswirkung auf das Ergebnis") oder dass Rechenoperationen mit der Null stets zum Ergebnis 0 führen.
Wie kann man solchen Schwierigkeiten im Umgang mit der Null im Unterricht begegnen?
Die Behandlung der Null im Unterricht ist umstritten. Volkert (1996) meint, dass die Null nicht verfrüht thematisiert werden sollte, da „vom Systematischen her kein zwingender Bedarf" bestehen würde (Volkert 1996, S. 103).
Vor allem sieht er ein Problem darin, dass die Null als Zahl nicht sinnvoll über Alltagsbezüge erarbeitet werden kann. Er kritisiert insbesondere (Schulbuch-)Aufgaben wie „In einem Käfig sind 5 Vögel. 5 fliegen weg. Wie viele bleiben übrig?". Denn Umschreibungen wie „keine" führen bei den Kindern in der Regel nicht zu der Einsicht, dass man hier zur Beantwortung der Frage eine Zahl braucht.
So kommt Volkert zu dem Schluss, dass die Einführung der Null als Zahl erst mit der Thematisierung des Dezimalsystems sinnvoll ist und orientiert sich somit an der geschichtlichen Entwicklung der Zahl Null (vgl. ebd.).
Auch Hefendehl-Hebeker (1981) und Hasemann (2007) sehen eine Einführung über Aufgaben wie die oben genannte kritisch. Dennoch erachten sie eine Erarbeitung der Null als Zahl bereits im ersten Schuljahr für notwendig, um Fehlvorstellungen (wie dem ‚Nichts-Charakter‘ der Null) von Anfang an entgegen zu wirken. Dieser Meinung schließt sich auch Padberg (2005) an.
Insbesondere Hefendehl-Hebeker plädiert dabei für einen natürlichen Zugang: „Dort, wo im Unterricht die Gelegenheit besteht, sind ihre Besonderheiten gegenüber anderen Zahlen in altersgemäßer Form herauszustellen" (Hefendehl-Hebeker 1981, S. 247). So bietet sich beispielsweise eine Art Umfrage an.
Die Kinder können aufgefordert werden abzuzählen, wie viele 5-Jährige, 6-Jährige, ..., 9-Jährige usw. in der Klasse sind und die Anzahlen entsprechend zu notieren. Auch hier muss man mit Antworten wie „keine" rechnen, aber hier bietet sich die sinnvolle Gelegenheit, deutlich zu machen, „dass die Null hier zum Aufschreiben einer Anzahl verwendet" (Hasemann 2007, S. 87 f.) und vor allem gebraucht wird.
Ergänzend kann der Zahlcharakter der Null noch weiter verdeutlicht werden, indem man bewusst über die Null als Rechenzahl spricht. Dies kann man mit Kindern z.B. an geeigneten schönen Päckchen thematisieren, in denen die Null sowohl als Operand als auch als Ergebnis auftritt (vgl. Hefendehl-Hebeker 1981, S. 247 ff.; Hasemann 2007, S. 87 f.):
5 – 4 = 1
5 – 3 = 2
5 – 2 = 3
5 – 1 = 4
5 – 0 = 5
Null als Subtrahend
6 – 1 = 5
6 – 2 = 4
…
6 – 6 = 0
Null als Ergebnis
5 – 5 = 0
6 – 4 = 2
7 – 3 = 4
8 – 2 = 6
…
Null als Ergebnis
0 + 1 =
0 + 2 =
0 + 3 =
0 + 4 =
0 + 5 =
Null als Summand
usw.
Verwandte Themen
Schöne Päckchen
Mehr zum mathematischen Hintergrund zum Rechnen mit der Null und damit bedingten Schwierigkeiten sowie typischen Fehlern finden Sie in:
Hefendehl-Hebeker, L. (1981). Zur Behandlung der Zahl Null im Unterricht, insbesondere in der Primarstufe. mathematica didactica, (4), 243-246.
Material
Aufgabenkarten
Literatur
