Im mathematischen Anfangsunterricht ist neben dem handelnden Umgang mit Materialien oder konkreten Erfahrungen zunächst das Arbeiten mit bildlichen Darstellungen ein wichtiges Mittel, um Zahl- und Operationsvorstellungen zu entwickeln.
Worauf man beim Einsatz bildlicher Darstellungen jedoch achten sollte und welche Schwierigkeiten dabei auftreten können, wird auf dieser Seite illustriert.
Welche Aufgabe passt zu dem Bild?

In einem Interview wird der Zweitklässlerin Luisa die obige Darstellung vorgelegt.
Es ergibt sich folgende Situation:
I: Hast du so ein Bild schon einmal gesehen?
L: Ich kann das nicht mehr so richtig. Ich konnte das mal ... vor den Ferien.
I: Welche Rechenaufgabe könnte denn zu diesem Bild passen?
L: Mmh, 9+13?
I: Warum passt das gut?
L: Weil hier ist ne 9 und hier 13 (zeigt auf die beiden Zahlen)... und von dort (zeigt auf die 9) tut man 13 dazu.
I: Ein anderes Kind meinte, 9+4 würde gut passen. Was meinst du dazu?
L: Nee, also die 4 ist ja hier (zeigt auf die 4) und die 9 da (zeigt auf die 9).
Eigenaktivität
Wie kommt Luisa zu ihrer Annahme? Es liegt doch auf der Hand, dass der Pfeil von der 9 zur 13 die Rechnung 9 + 4 = 13 veranschaulichen soll. Oder?
Chancen und Probleme des Einsatzes bildlicher Darstellungen
Eine wesentliche Aufgabe des Mathematikunterrichts in der Grundschule ist der Aufbau grundlegender Zahl- und Operationsvorstellungen. Dafür ist ein sicheres Bewegen auf und zwischen allen Darstellungsformen (handelnd, bildlich, sprachlich und symbolisch) unumgänglich.
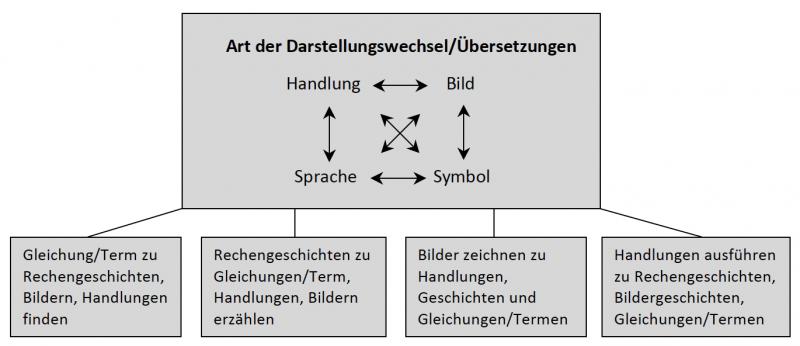
(Kaufmann & Wessolowski 2006, S. 25)
Mathematische Begriffe und Operationen können durch Handlungen mit Material, durch Bilder, Sprache und mathematische Symbole dargestellt werden. Die verschiedenen Darstellungen stellen einerseits eine wichtige Lernhilfe dar, andererseits sind sie aber auch Lerngegenstand mit eigenen Anforderungen für die Schülerinnen und Schüler, die Bedeutungen und Formen des Gebrauchs erlernen müssen.
Letzteres ist ein wesentlicher Aspekt beim Einsatz bildlicher Darstellungen.
So wichtig sie für die Entwicklung von Zahl- und Operationsvorstellungen auch sind, Veranschaulichungen stellen immer auch einen neuen Lernstoff für die Schülerinnen und Schüler dar, der insbesondere für leistungsschwächere Kinder eine neue Lernhürde sein kann. Des Weiteren sind Veranschaulichungen prinzipiell mehrdeutig:
Sie rufen nicht (wie es in vielen Schulbüchern erwartet wird) automatisch und zweifelsfrei die Deutung des Bildes in Form eines ganz bestimmten Zahlensatzes bei den Kindern hervor.
In den Schulbüchern findet man eine Vielzahl an bildlichen Darstellungen, die Zahlen und Operationen über konkrete Dinge oder Situationen veranschaulichen. Der Einsatz dieser Veranschaulichungen ist in der Grundschule unentbehrlich, bedarf aber großer Sensibilität und Bewusstheit.
Eigene Erkundung zu bildlichen Darstellungen
Eigenaktivität
Bevor Sie sich im Folgenden damit auseinander setzen, wie Erst- und Zweitklässler bildliche Darstellungen deuten, schauen Sie sich zunächst selbst einmal diese Bilder an.
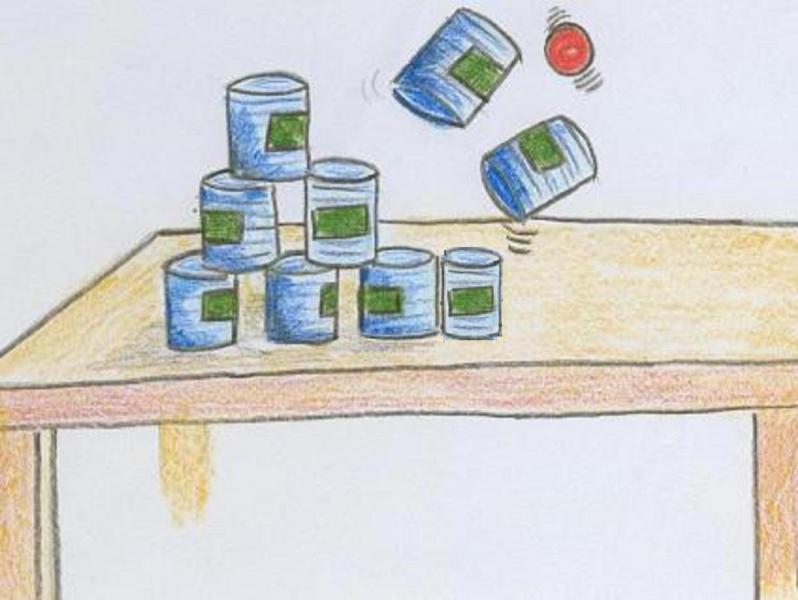
Dosenwerfen

Entchen (Köpfchen unter Wasser)

Punktmengen
- Welche passende Rechenaufgabe kommt Ihnen beim Betrachten der einzelnen Bilder als erstes in den Sinn? Wie könnte man sie noch deuten?
- Welche Interpretationen der Bilder erwarten Sie bei Erst- und bei Zweitklässlern? Begründen Sie Ihre Annahme.
So deuten Kinder bildliche Darstellungen
Die folgenden Videos zeigen exemplarisch, wie Erst- und Zweitklässler die drei Bilder tatsächlich gedeutet haben. Sie illustrieren noch einmal, dass Veranschaulichungen für Kinder nicht so eindeutig und selbstverständlich sind, wie wir (oder Schulbücher) es möglicherweise erwarten.
Möglicherweise werden Sie einige Reaktionen der Kinder auch überraschen. Dies kann manchmal auch an der Veranschaulichung selbst liegen. Der Einsatz von bildlichen Darstellungen wirft deshalb immer auch Fragen auf, wie z.B.: Ist die Veranschaulichung wirklich klar, eindeutig und selbsterklärend? Macht sie (für die Kinder) Sinn?
Schauen Sie sich dazu die mitunter sehr kreativen Interpretationen der Kinder zu dem Punktmengenbild an:
Punktmengen
Insbesondere das Nennen/Aufschreiben einer passenden Rechnung zu Veranschaulichungen der Subtraktion stellt für einige Kinder eine Schwierigkeit dar. Beobachten Sie beispielsweise die Kinder in diesem Video zum Bild "Dosenwerfen":
Dosenwerfen
Sie werden beim Betrachten der Videos festgestellt haben, dass die Kinder auch dieses Bild unterschiedlich deuten. Einige Kinder erklären die Situation Dosenwerfen so wie intendiert und nennen auch die entsprechende Rechenaufgabe. Andere Kinder erklären zwar die Situation vollkommen richtig, geben im Anschluss daran jedoch nicht die Rechenaufgabe an, die zu ihren Erklärungen und zu dem Bild eigentlich passen würde.
Sobald sie den Kontext "Dosenwerfen" verlassen und nur noch die passende Rechenaufgabe nennen sollen, versuchen sie, die Anzahl der Zahlen miteinander zu verknüpfen. Die Gesamtmenge der Dosen, die vor dem Wurf aufgebaut war, lassen sie dann außer Acht. Teilweise deuten die Kinder die Operation auch gar nicht so, wie sie gedacht ist (als eine typische Subtraktionssituation), sondern als Addition.
Interessante Erklärungen von Kindern, warum die im Schulbuch erwartete Aufgabe 6-6=0 zum Entenbild ihrer Meinung nach nicht passt, können Sie sich hier anschauen:
Enten (Köpfchen unters Wasser)
Die Videos sollen nicht den Eindruck erwecken, dass Veranschaulichungen von Rechenoperationen unsinnig sind. Im Gegenteil: Sie sind in der Grundschule ein wesentlicher Bestandteil zur Entwicklung grundlegender Zahl- und Operationsvorstellungen. Die Videos sollen vielmehr zeigen, dass Lehrerinnen und Lehrer bei Auswahl und Einsatz sensibel und bewusst vorgehen sollten.
Hier finden Sie noch weitere Videos zur eigenen Analyse:
Kirschen
Wippe
Schmetterlinge
Würfelbilder
Weiterführende Aufgaben
Sichere Zahl- und Operationsvorstellungen zeigen sich durch ein sicheres Bewegen auf und zwischen den verschiedenen Darstellungsformen (vgl. Abbildung aus Abschnitt 2). Bei den oben aufgeführten Beispielen handelt es sich um die Übersetzung von der ikonischen in die symbolische Darstellungsform.
Im Folgenden soll nun auch die Übersetzung von der symbolischen in die ikonische Darstellungsform betrachtet werden. Radatz hat dazu 1989 eine Untersuchung (vgl. Radatz 1989) zu den Vorstellungen bzw. Vorstellungsbildern von Kindern zu den Rechenoperationen Addition und Subtraktion durchgeführt.
Bevor Sie sich dazu mit Kinderdokumenten auseinander setzen, informieren Sie sich bitte hier über diese Untersuchung.
In Anlehnung an die Untersuchung von Radatz haben auch wir Kindern die Aufgabe gestellt: "Male/Zeichne ein Bild zu der Aufgabe 7 - 2 = 5 (bzw. 4 + 3 = 7). Auch ein chinesisches Kind, das unsere Zahlen und Buchstaben nicht kennt, soll es verstehen können." Hier finden Sie verschiedene Kinderdokumente dazu:
Bildliche Darstellungen: Kinderdokumente
Eigenaktivität
Versuchen Sie, die Darstellungen der Kinder nachzuvollziehen. Was hat sich das Kind bei seiner Darstellung wahrscheinlich gedacht?
Ordnen Sie Darstellungen der Kinder den vier Hauptklassen nach Radatz zu. Begründen Sie Ihre Zuordnung.
Wenn Sie Ihre Zuordnung überprüfen möchten, finden Sie hier eine mögliche Lösung.
Verwandte Themen
Rechnen im 20er-Raum
Veranschaulichungen als "neuer Lernstoff" und "Mehrdeutigkeit"
Materialien
InterviewleitfadenInterviewprotokoll bildliche Darstellungen
Literatur
