Die halbschriftliche Division ist die letzte halbschriftliche Rechenstrategie, die die Kinder im Mathematikunterricht erlernen. Auf dieser Seite bekommen Sie die Möglichkeit, sich mit den verschiedenen Vorgehensweisen und Schwierigkeiten der Kinder bei Aufgaben zur halbschriftlichen Division auseinanderzusetzen und diese anhand von Schülerdokumenten, die im Rahmen einer Studie von Pletz & Sperling (2010) entstanden sind, zu analysieren.
Eine Aufgabe - viele verschiedene Lösungswege!
Wie unterschiedlich die Kinder die Eigenheiten der Zahlen ausnutzen und so zu verschiedenen Rechenwegen gelangen, können Sie am folgenden Beispiel erkennen:
Eigenaktivität
Schauen Sie sich die Vorgehensweisen der Kinder an und versuchen Sie, die Besonderheiten dieser nachzuvollziehen.
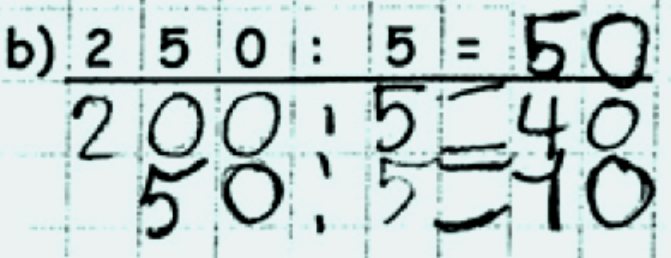
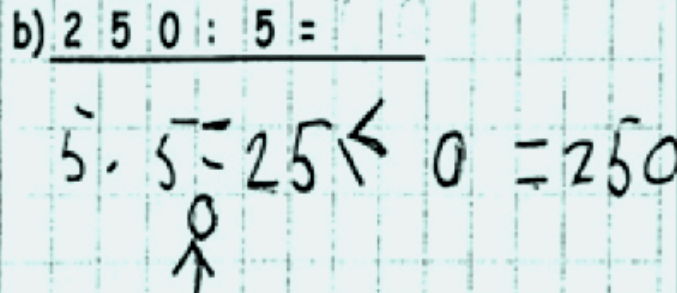


Hintergrundwissen zum halbschriftlichen Rechnen
Bei sehr großen Zahlen oder bei einer wachsenden Anzahl von erforderlichen Merkprozessen stoßen die Kinder beim Kopfrechen in absehbarer Zeit an ihre Grenzen. An dieser Stelle ist es sinnvoll, Teilschritte oder Zwischenergebnisse zu notieren, wobei die jeweiligen Vorgehensweisen sowie Art und Umfang der Notizen zu Beginn sehr unterschiedlich sind. „Diese Notizen unterstützen das Kopfrechnen" (Padberg 2005, S. 159).
In der Literatur wird diese Art des Rechnens als halbschriftliches Rechnen bezeichnet. Beim halbschriftlichen Rechnen ist keine bestimmte Notationsform vorgeschrieben. Vor allem sollten die Besonderheiten der Zahlen ausgenutzt und flexible Rechenstrategien eingesetzt werden. Dies ist nur möglich, da es sich um ein Rechnen mit Zahlenganzheiten handelt (vgl. Padberg & Benz 2011, S. 170).
Das halbschriftliche Rechnen bietet eine Verknüpfung des mündlichen Rechnens mit dem schriftlichen und dient dabei als Grundlage für die Einführung des schriftlichen Rechnens. Diese Notationsformen helfen, „die dem Algorithmus zugrunde liegenden Regelhaftigkeiten aufzudecken [und] seine Systematik wirklich mit Sinn zu füllen" (Krauthausen 1995, S. 15).
Typische Vorgehensweisen bei der halbschriftlichen Division
Bei der halbschriftlichen Division unterscheidet man zwei Hauptstrategien: das schrittweise Rechnen und die Hilfsaufgabe. Während die Strategie ''Schrittweise'' universell einsetzbar ist, bietet sich die Nutzung einer Hilfsaugabe zwar oftmals, aber nicht immer an (vgl. Padberg & Benz 2011, S. 188 f.).
Des Weiteren gibt es die Strategien des gleichsinnigen Veränderns (vgl. Graumann 2002, S. 59 f.) sowie der Umkehraufgabe.
Diese Strategien werden aber nur sehr selten genutzt, da sie sich für die meisten Aufgaben überhaupt nicht anbieten. Viele Kinder entdecken zudem ihre eigenen Wege, sodass Mischformen verschiedener Strategien entstehen (vgl. Krauthausen 1995, S. 15).
Im Folgenden werden die einzelnen halbschriftlichen Divisionsstrategien verdeutlicht.
1. Schrittweise
Hier gibt es zwei Schreibweisen. Eine, die auf die additive Zerlegung des Dividenden hinweist und eine weitere, die auf der multiplikativen Zerlegung des Divisors beruht.
Beispiel:
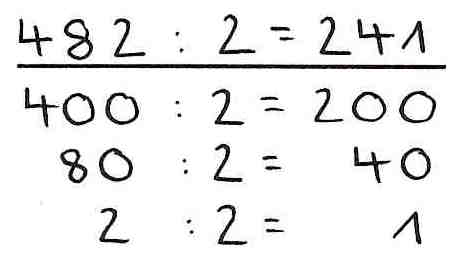
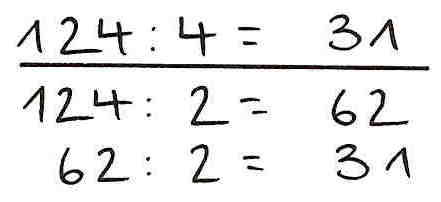
2. Hilfsaufgabe
Die Hilfsaufgabe ist eine ähnliche Aufgabe, die jedoch einfacher zu lösen ist. Hierbei nutzt man meist benachbarte oder Analogieaufgaben.
Beispiel:
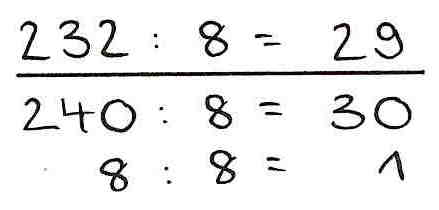
3. Vereinfachen
Der Dividend und der Divisor sind durch die gleichen Zahlen teilbar bzw. lassen sich mit der gleichen Zahl multiplizieren, ohne dass sich das Ergebnis ändert.
Beispiel:
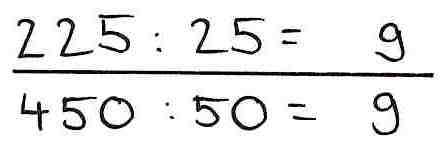
4. Umkehraufgabe
Hierbei wird aus der Divisionsaufgabe die passende Multiplikationsaufgabe gebildet.
Beispiel:
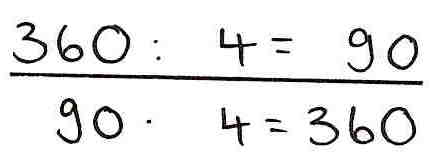
Hier finden Sie eine mögliche Zuordnung.
Typische Fehler bei der halbschriftlichen Division
Allgemein ist festzuhalten, dass es gerade bei der halbschriftlichen Division oftmals viele verschiedene und sehr individuelle Fehler auftreten. Im Rahmen der Studie von Pletz & Sperling (2010) konnten einige mehr oder weniger typische Fehler der Kinder ausgemacht werden. Nachfolgend können Sie die vorkommenden Fehler der Kinder sehen.
1. Verständnisfehler - ungünstige Zerlegung des Dividenden
In diesem Beispiel wird der Dividend so zerlegt, dass sich Teilrechnungen ergeben, die nicht ohne Rest gelöst werden können. Aus diesem Grund wird der Rechenweg häufig abgebrochen und nicht fortgeführt.
Beispiel:
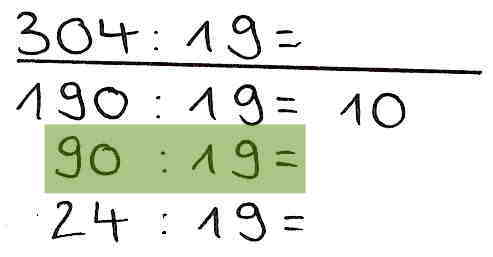
2. Verständnisfehler - gegensinniges Verändern von Dividend und Divisor
Das Gesetz von der Konstanz des Quotienten wird falsch angewendet, wenn Dividend und Dividor nicht gleichsinnig verändert werden.
Beispiel:
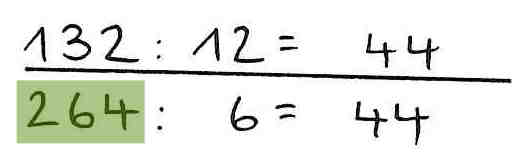
3. Verständnisfehler - fehlerhafte Verknüpfung von Teilergebnissen
Trotz korrekter Zerlegung des Divisors (2 ⋅ 4 = 8) sowie korrekter Ausführung der einzelnen Teilrechungen werden die Zwischenergebnisse verknüpft (116 - 29 = 87), obwohl bereits 29 das Endergebnis darstellt.
Beispiel:
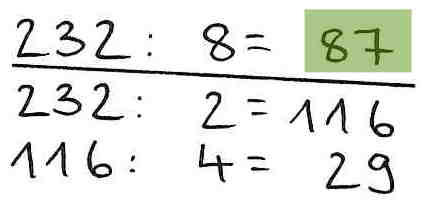
4. Rechenfehler - fehlerhaftes Streichen von Nullen
Bei diesem Beispiel ist das Ergebnis nicht stellengerecht, da bei der Division glatter Hunderter- und Zehnerzahlen vergessen wurde, eine weitere Null zu streichen.
Beispiel:
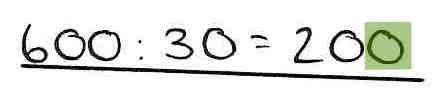
Eigenaktivität
Betrachten Sie die unten abgebildeten fehlerhaften Kinderdokumente und versuchen Sie zu verstehen, wie die Kinder zu ihren Lösungen gekommen sind.
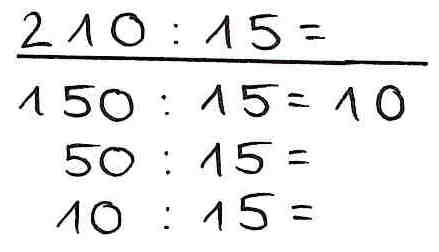
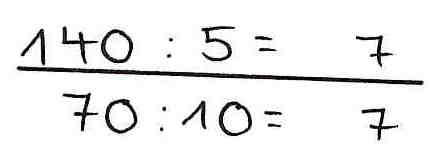
Hier finden Sie eine mögliche Erklärung.
Analyse des sinnvollen und flexiblen Strategieeinsatzes
Ein flexibler Einsatz von Rechenstrategien ist sinnvoll, da es häufig Aufgaben gibt, die sich mit einer bestimmten Strategie besonders leicht lösen lassen; eine andere Strategie hingegen kann sich bei dieser Aufgabe als besonders umständlich erweisen.
Deshalb sollten die Kinder möglichst viele verschiedene Strategien zum Lösen von Aufgaben kennen und auch einsetzen können. Natürlich nutzen Kinder gerne die Strategie, die für sie am einfachsten anwendbar ist, um mit dieser alle Aufgaben schnell lösen zu können. Dabei stoßen sie jedoch teilweise rasch an ihre Grenzen.
So ist es wichtig, dass die Kinder viele Rechenstrategien kennenlernen, damit sie bei den für die jeweilige Strategie sinnvollen Aufgaben die einfachste Strategie anwenden und so flexibel und sinnvoll rechnen können.
Eigenaktivität
Überlegen Sie zunächst selbst: Welche der oben genannten Strategien erweisen sich zur Berechnung der folgenden Aufgaben als besonders sinnvoll? Welche erweisen sich wahrscheinlich als problematisch? Warum?
57:3=
96:8=
72:8=
250:5=
133:7=
909:9=
396:4=
Hier sehen Sie eine beispiehafte Analyse.
Testen Sie Ihr Wissen zu dem Thema in unserem Kira-Check.
Verwandte Themen
Halbschriftliche Subtraktion
Halbschriftliche Addition
Aufteilen und Verteilen
Multiplikation und Division
Flexibles Rechnen
Schriftliche Division
Wollen Sie noch mehr über die Vorzüge des halbschriftlichen Rechnens erfahren, schauen Sie auf der Seite zur halbschriftlichen Addition nach.
In der Studie von Pletz & Sperling (2010) wurde mit 123 Kindern eine Standortbestimmung zur halbschriftlichen Division durchgeführt (die konkrete Standortbestimmung finden Sie unten). Es konnte festgestellt werden, dass viele der befragten Kinder auf die Strategie "Schrittweise" zurückgegriffen haben. Bei Aufgaben, die die Strategie "Hilfsaufgabe" nahelegten (z.B. 152:8 oder 57:3), haben die Kinder oftmals den Vorteil dieser Strategie erkannt und das eigentliche Ergebnis aus einer Hilfsaufgabe abgeleitet.
Arbeitsblatt Hauptstudie
Darüberhinaus haben einige Kinder auch Mischformen und Umkehraufgaben zur Lösung herangezogen. Manche Kinder haben leider keine Zwischenrechnungen notiert, sodass diese als "im Kopf gelöst" verzeichnet wurden.
Wenn Sie noch weitere Details zur Auswertung dieser 123 Standortbestimmungen erfahren wollen, können Sie hier nachsehen.
Die meisten Erwachsenen kennen aus der Schule entweder nur die schriftlichen Rechenverfahren oder nutzen im Alltag intuitiv halbschriftliche Vorgehensweisen. Als Lehrperson mit dem Fach Mathematik sollten Sie allerdings die große Vielfalt halbschriftlicher Rechenverfahren kennen und im Unterricht mit Blick auf die individuellen Vorlieben der Lernenden die eine oder andere Strategie thematisieren.
Das stellt fachfremd Unterrichtende vor eine große Herausforderung, da sie selbst in ihrer damaligen Schulzeit nur auf die schriftlichen Rechenverfahren eingetrimmt wurden. Besuchen Sie deshalb die Homepage des Projekts PriMakom („Primarstufe Mathematik kompakt“).
Dabei handelt es sich in erster Linie um eine Selbstlernplattform für Lehrerinnen und Lehrer, die Mathematik fachfremd unterrichten und sich somit fachdidaktische Kenntnisse in kompakter Form aneignen möchten. Dort erhalten Sie kompakte Hintergrundinformationen, sowie unterrichtspraktische Hinweise zu den halbschriftlichen Rechenstrategien: primakom: Inhalte: Zahlen und Operationen: Halbschrichtliches Rechnen: Einstieg.
Material
Standortbestimmung zur halbschriftlichen Division
Literatur
© Stefanie Pletz und Sabrina Sperling für das KIRA-Team
