Um mehr über die mathematischen Denkwege von Kindern zu erfahren, bedarf es besonderer Methoden wie z.B. Standortbestimmungen oder diagnostischer Gespräche. Mit der Methode allein ist es aber noch nicht getan. Der Einsatz solcher diagnostischer Methoden erfordert immer auch eine sorgfältige Aufgabenauswahl.
Rein produktorientierte Aufgaben, bei denen es nur um 'richtig' oder 'falsch' geht, ermöglichen dem Lehrer nur selten Einblicke in die Denkwege der Kinder und es ist kaum möglich, bei Fehllösungen festzustellen, ob diese "nur" auf mangelnder Konzentration oder auf Fehlvorstellungen beruhen. Gut eignen sich hingegen sogenannte "informative Aufgaben", bei denen man, wie es der Name schon sagt, mehr Informationen über die Denkwege der Kinder erhält.
Die Eigenschaften solcher Aufgaben sowie Beispiele sollen auf dieser Seite vorgestellt werden.
Informativ oder nicht?
Eigenaktivität
Inwiefern handelt es sich bei dieser Aufgabe um eine informative Aufgabe?
Was erfahren Sie anhand des Dokuments über Thomas Kompetenzen im Bereich der schriftlichen Subtraktion?

Thomas Lösung der Aufgabe
Hintergrundwissen zu informativen Aufgaben
"Durch informative Aufgaben kann man mehr über die Lösungswege der Kinder erfahren als durch herkömmliche Aufgaben. Auf dieser Grundlage können weitere Fördermaßnahmen auf individuellem Niveau eingeleitet werden.
Daher sollte in erkennbarer Nähe zu den Aufgabenstellungen Platz für Nebenrechnungen oder Erläuterungen zur Verfügung stehen oder explizit die Aufforderung erfolgen, das eigene Vorgehen zu erläutern.
Eine überlegte Aufgabenauswahl (etwa bezüglich des Schwierigkeitsgrades der Teilaufgaben, des Grades der Ähnlichkeit bzw. des Zusammenhangs oder der verwendeten Kontexte) kann darüber hinaus den Informationsgehalt von Aufgaben steigern" (Sundermann, B. & Selter, Ch. 2006, S. 79).
Idealtypisch gibt es, wie im obigen Zitat angedeutet, vier Formen informativer Aufgaben, die im Folgenden kurz dargestellt werden sollen.
Aufgabenvariationen
Von Fall zu Fall kann es sein, dass ein Kind eine Aufgabe lediglich in bestimmten Zusammenhängen beherrscht bzw. in manchen Kontexten etwas leisten kann, was es in anderen nicht zeigt. Das heißt, dass die Veränderung der Darstellung einer Aufgabe zu verschiedenen Vorgehensweisen führen kann. Konkret bedeutet das hier: Wie löst das Kind die Aufgabe 12:3 einmal in dem Kontext einer Bild-Sach-Aufgabe und einmal rein symbolisch?

(Hengartner & Röthlisberger 1999, S. 40)
Nebenrechnungen
Nebenrechnungen geben zusätzlich zu den Ergebnissen Einsicht in die Lösungswege und Fähigkeiten der Kinder. So wird im Beispiel deutlich, dass Sofia im Gegensatz zu Paul zwar alles richtig gerechnet hat, sie scheint aber weniger "Zahlensinn" zu haben als er: Sie subtrahiert jede Aufgabe erneut schriftlich, während Paul die Zusammenhänge zwischen den Aufgaben nutzt, um die Ergebnisse zu ermitteln. Dies wird erst durch die Nebenrechnungen der Kinder deutlich.

(Sundermann & Selter 2006, S. 86 f.)
Vorgehensweisen darstellen
Wenn man Kinder dazu auffordert, ihre Vorgehensweisen darzustellen, eröffnen sich häufig interessante Einblicke in ihre Denkwege. So wird im folgenden Dokument erst durch die Begründung des Kindes deutlich, dass es die Zusammenhänge zwischen den Aufgaben entdeckt und ausnutzt, was nicht selbstverständlich ist - auch wenn man dabei berücksichtigen muss, dass nachträgliche Erklärung und tatsächliches Vorgehen nicht immer übereinstimmen.
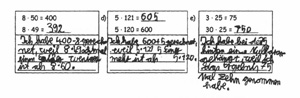
(Sundermann & Selter 2006, S. 88)
Zusammenhängende Aufgaben
Will man die Fehlermuster von Schülerinnen und Schülern aufdecken sowie verstehen, eignen sich zusammenhängende Aufgaben besonders gut. Dazu werden anhand bestimmter Kriterien systematisch Aufgaben zusammengestellt. Mögliche Kriterien sind beispielsweise aufgabentypische Schwierigkeitsmerkmale (vgl. dazu Abschnitt 3) oder die Verwandtschaft von Aufgaben (z.B. 5·90, 90·5, 450:5, 4500:50 usw.).
Sie werden im Einstiegsbeispiel festgestellt haben, dass man durch diese einzelne Schülerlösung kaum eine Aussage über Thomas Kompetenzen hinsichtlich der schriftlichen Subtraktion machen kann. So vermittelt das Dokument zunächst einmal den Eindruck, dass Thomas die schriftliche Subtraktion beherrscht, denn es sind keine Fehler zu entdecken.
Betrachtet man die Aufgabe jedoch genauer, so fällt auf, dass die Aufgabe keinerlei Stolpersteine in sich birgt - typische Fehler, wie z.B. Fehler mit dem Übertrag, können bei dieser Aufgabe gar nicht begangen werden.
Wir erfahren anhand dieses Dokuments also nur, dass Thomas in der Lage ist, schriftliche Subtraktionsaufgaben ohne jeglichen zusätzlichen Schwierigkeitsfaktor korrekt zu lösen. Über alles weitere erlaubt das Schülerdokument keine Aussage. Diese Aufgabe allein eignet sich also nicht, um etwas über Thomas Denk- und Rechenwege zu erfahren.
Zusammenhängende Aufgaben am Beispiel der schriftlichen Subtraktion - Videoanalyse
Am Beispiel von Thomas soll im Folgenden aufgezeigt werden, dass eine systematische Aufgabenauswahl hilft, bestimmte Fehler besser nachvollziehen zu können bzw. einen Hinweis darauf zu bekommen, ob es sich nur um einen Flüchtigkeitsfehler handelt oder um ein konsequentes Fehlermuster. Insbesondere bei der schriftlichen Subtraktion sind Fehler häufig abhängig von dem jeweils angewandten Algorithmus.
Im Folgenden zeigen wir Ihnen verschiedene Dokumente, in denen Thomas Aufgaben zur schriftlichen Subtraktion löst. Einige dieser Aufgaben löst er richtig, andere fehlerhaft.
Eigenaktivität: Betrachten Sie das Video bzw. Schülerdokument zur Lösung der Aufgabe 701 - 698 von dem Viertklässler Thomas, der das Ergebnis 103 anstelle von 3 ermittelt.*
Thomas
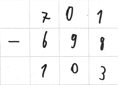
Wenn Sie sich wundern, dass Thomas diese Aufgabe überhaupt schriftlich rechnet, obwohl es doch viel leichter wäre durch die Nähe von Minuend und Subtrahend (im Kopf) zu ergänzen: Wir haben die Kinder diese Aufgabe ganz bewusst schriftlich lösen lassen, da die Aufgabe in diesem Zusammenhang durch die erforderlichen Überträge und die Null besonders fehleranfällig ist. Im Übrigen betrachten wir den fehlenden Strich, der das Gleichheitszeichen ersetzt, hier nicht als Fehler.
Hier finden Sie eine mögliche Interpretation zu Thomas Lösung 701 - 698 = 103.
Eigenaktivität: Betrachten Sie nun die weiteren Schülerdokumente bzw. Videos.
Inwiefern bestätigen sich die obigen Vermutungen?

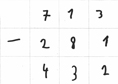



Hier finden Sie eine mögliche Interpretation.
Verwandte Themen
- Diagnostische Gespräche
- Orientierung im Hunderterraum
- Schriftliche Subtraktion
- Verfahren schriftlicher Subtraktion nach Padberg (2005)
PIKAS: Lernstände wahrnehmen
PIKAS: Aufgaben adaptieren
primakom: Leistungen feststellen
Übersicht zu den verschiedenen Verfahren der schriftlichen Subtraktion z.B. bei:
Padberg, F. (2005). Didaktik der Arithmetik für Lehrerausbildung und Lehrerfortbildung, S. 221-250.
