Das Ziel eines jeden Unterrichts sollte die bestmögliche Förderung aller Kinder sein. Auch wenn Kinder manchmal Fehler machen oder Schwierigkeiten haben, sollte man nicht nur diese Fehler im Blick haben. Die Kinder machen zugleich auch vieles richtig, auf das man im weiteren Unterrichtsverlauf aufbauen kann, sodass die Kinder eine zielgerichtete Förderung erhalten.
Denn erst wenn die Ursachen der Schwierigkeiten und Fehler mit Hilfe des kompetenzorientierten Blicks erkannt werden, kann man die Kinder gezielt fördern, sodass sie ihre Fehler überwinden können (vgl. Sundermann & Selter 2006, S.13 f.).
Auf dieser Seite werden Sie wesentliche Hintergrundinformationen zum Thema schriftliche Addition bekommen. So erhalten Sie einen Überblick über wichtige Voraussetzungen zur Einführung des Themas. Des Weiteren werden Sie mit den typischen Fehlermustern der schriftlichen Addition vertraut gemacht werden, sodass Sie im Anschluss daran Ihren kompetenzorientierten Blick und Ihre Diagnosefähigkeit anhand verschiedener Schülerdokumente testen können.
Sophia rechnet schriftlich 876+145
Im Beispiel sehen Sie, wie Sophia die Aufgabe 876+145 löst.
Eigenaktivität
Wie könnte Sophia zu dem Ergebnis gekommen sein? Was vermuten Sie?
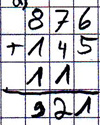
Hier finden Sie eine kompetenzorientierte Analyse von Sophias Lösung.
Hintergrundwissen zur schriftlichen Addition
Das erste schriftliche Rechenverfahren, das die Kinder in der Schule lernen und anwenden ist die schriftliche Addition. Vor einigen Jahren war es wichtig, dass die Schülerinnen und Schüler dieses Verfahren „im Schlaf" ausführen konnten (vgl. Schipper 2009, S. 180).
Heute jedoch - im Zeitalter des Taschenrechners und des Computers - wird viel mehr Wert darauf gelegt, dass die Kinder das Verfahren verstehen, dass sie Beziehungen der Mathematik in den Aufgaben entdecken können und dass sie sich bewusst machen, warum es manchmal nicht sinnvoll ist, mit diesem Verfahren zu rechnen (z.B. bei Aufgaben wie 199+2 oder auch 252+41).
Vergleicht man den Algorithmus der schriftlichen Addition, mit denen der schriftlichen Subtraktion, Multiplikation oder Division, dann steht fest, dass er der unkompliziertere Algorithmus ist (vgl. Radatz u.a. 1999, S. 121).
Dennoch können verschiedene Fehler bei den Kindern auftreten, wenn sie den Algorithmus mechanisch ausführen können, ihn jedoch nicht verstanden haben. Deswegen ist es von großer Wichtigkeit dass die Kinder, bevor sie den Algorithmus lernen, das kleine Einspluseins gut und sicher beherrschen.
Ebenso muss das Verständnis des Bündelungsprinzips und der Stellenschreibweise gefestigt sein (vgl. Radatz u.a. 1999, S. 120), da die schriftliche Addition an die Vorkenntnisse der Schülerinnen und Schüler im Bereich der halbschriftlichen Addition anknüpft (vgl. Fuchs u.a. 2005, S. 139). Dennoch müssen die Kinder einen neuen Zahlensinn entwickeln, da das schriftliche Rechnen ein reines Ziffernrechnen ist (vgl. Aster 2005, S. 232).
So verlangt z.B. der Lehrplan für das Land NRW, dass die Schülerinnen und Schüler das Verfahren nicht nur sicher ausführen können, sondern es auch verstehen, sodass sie das Verfahren mit eigenen Worten erläutern können (vgl. MSW NRW, S. 62).
Deswegen ist es unverzichtbar, dass die Lehrperson die Vorgehensweisen der Kinder nachvollziehen kann, um eine bestmögliche Förderung für jedes Kind zu ermöglichen.
Die Schreibweise der schriftlichen Addition wurde nicht wie bei der Subtraktion, Multiplikation und Division explizit festgelegt, ist aber, bis auf ein paar kleine Unterschiede, international weitestgehend gleich (vgl. Padberg & Benz 2011, S. 227).
Typische Fehler und Schwierigkeiten
Die schriftliche Addition ist das einfachste schriftliche Rechenverfahren und viele Kinder scheinen es schnell und richtig anwenden zu können. Bei manchen Kindern aber tauchen gehäuft typische Fehler auf, die oftmals als Flüchtigkeitsfehler akzeptiert werden, obwohl sie oft nicht durch Flüchtigkeit entstanden sind und deswegen thematisiert werden müssten (vgl. Gerster 1982, S. 14), da sich sonst die Fehler bei den Schülerinnen und Schülern festigen könnten.
Durch diese Ignoranz der individuellen Schwierigkeiten mit dem schriftlichen Additionsalgorithmus wird gleichzeitig das Richtigstellen des Fehlers erschwert. Aus diesem Grund ist es notwendig, dass die Lehrperson mit Hilfe informativer Aufgaben das Verständnis der Kinder bzgl. der schriftlichen Addition ermittelt.
Damit die Lehrperson die Schwierigkeiten ihrer Schülerinnen und Schüler erkennt und im Unterricht thematisieren kann, ist es enorm wichtig, dass sie die Schülerdokumente nachvollziehen kann und ihr die typischen Fehler der schriftlichen Addition bekannt sind.
Im Folgenden werden Sie einige Schülerdokumente sehen, in denen sich typische Fehler der schriftlichen Addition verbergen (in Anlehnung an Gerster 1982; Padberg & Benz 2011, S. 230 f.).
Fehlertyp:
Die Berechnung wird von links nach rechts durchgeführt. Die Überträge werden dabei in die falsche Stellenwertspalte übertragen.
Beispiel: 360 + 49

Fehlertyp:
Falsches Stellenwertverständnis: Die Summanden der Aufgabe werden nicht stellengerecht untereinander notiert.
Beispiel: 587 + 34
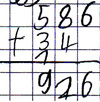
Fehlertyp:
Falsches Stellenwertverständnis: Hinzufügen einer Ziffer an die Einerstelle
Beispiel: 77 + 985
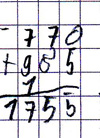
Fehlertyp:
Subtraktion statt Addition
Beispiel: 583 + 228

Fehlertyp:
Der Übertrag wurde an der falschen Stelle notiert.
Beispiel: 370 + 38
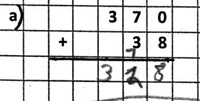
Fehlertyp:
Kein Übertrag zur Null
Beispiel: 908 + 406
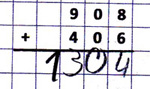
Fehlertyp:
Es wurde ein Übertrag zu viel notiert.
Beispiel: 481 + 315
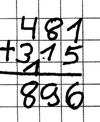
Fehlertyp:
Übertrag vergessen
Beispiel: 876 + 145
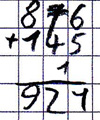
Fehlertyp:
An der Leerstelle/zusätzlichen Stelle wird kein Übertrag notiert.
Beispiel: 805 + 309
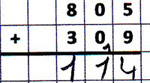
Fehlertyp:
Probleme beim Rechnen mit der Null (0 + x = 0)
Beispiel: 360 + 49
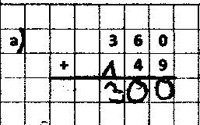

Fehlertyp:
Rechenfehler beim kleinen Einspluseins
Beispiel: 586 + 34
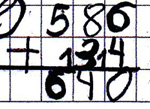
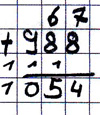
Fehlertyp:
Um 1 verrechnet, vermutlich durch falsches Weiterzählen
Beispiel: 67 + 988
Eigenaktivität
- Vermuten Sie, wie häufig die einzelnen Fehlertypen auftreten. Welche Fehler werden wohl sehr häufig zu finden sein? Welche eher selten?
- Ändern sich die Fehlerhäufigkeiten, wenn die Aufgaben aus einem für die Kinder unbekannten Zahlenraum stammen? Was vermuten Sie? Wie begründen Sie Ihre Vermutung?
Hier sehen Sie die Ergebnisse einer Bachelorarbeit von Beyoglu und Kötterheinrich (2010), die sich genau mit dieser Thematik beschäftigt hat.
Für die Lehrperson ist es nicht nur wichtig, dass ihr die einzelnen Fehlertypen bekannt sind, sondern sie diese auch erkennt und auf mögliche Ursachen zurückführen kann. Dabei ist es aber notwendig, dass vergleichbare Aufgaben bearbeitet werden, durch die die Lehrperson in der Auswertung erkennen kann, ob bei einem Schüler lediglich durch Flüchtigkeit Fehler entstanden sind, oder im Gegensatz dazu bestimmte Aufgaben oder Teilaufgaben systematisch fehlerhaft bearbeitet wurden.
Damit jeder Schüler individuell gefördert werden kann, bedarf es einer regelmäßigen Standortbestimmung, die der Lehrperson „strukturierte Informationen über Kompetenzen und Defizite einzelner Kinder" (Sundermann & Selter 2006, S. 21) geben und zur Planung des weiteren Unterrichtsverlaufs herangezogen werden kann.
Der Übertrag
Wie Sie bereits in Kapitel 3 erfahren haben, entstehen sehr viele Fehler durch fehlende, nicht beachtete oder zu viel notierte Überträge. Für das Verstehen und Anwenden des Verfahrens ist es wichtig, dass die Kinder wissen, wann ein Übertrag entsteht und auch was die kleine Übertragseins bedeutet.
Im Folgenden sehen Sie einige schriftliche Erklärungen von Schülerinnen und Schüler einer 3. Klasse zur Aufgabe „Erkläre, warum man manchmal eine 1 übertragen muss.". Bedenken Sie, dass es gewiss nicht einfach ist, eine schriftliche Erläuterung zum Übertrag zu geben.
Für die Kinder ist dies eine hohe Kompetenzanforderung, die je nach Leistungsstärke der Schüler unterschiedlich ausfällt. Doch wenn man genau hinschaut, kann man oftmals auch aus nicht eindeutigen Antworten erkennen, dass die Kinder das Richtige gemeint haben könnten.
Eigenaktivität
- Versuchen Sie mit eigenen Worten zu erklären, warum man manchmal eine 1 übertragen muss. Schauen Sie sich die Schülerdokumente an und vergleichen Sie Ihre Lösung mit denen der Schüler. Gibt es Ähnlichkeiten?
- Bei welchen Dokumenten würden Sie vermuten, dass das Kind verstanden hat, warum es manchmal eine 1 übertragen muss? Begründen Sie Ihre Vermutung.
- Wie würden Sie die Übertragseins im Unterricht thematisieren, nachdem Sie durch eine Standortbestimmung festgestellt haben, dass vermutlich noch nicht alle Kinder verstanden haben, was die Übertragseins bedeutet?

Michelle

Mareike

Jan
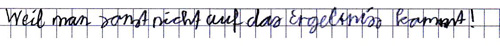
Lukas
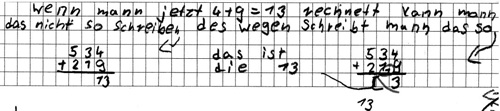
Lareen

Stefan

Timo
Analyse verschiedener Schülerdokumente
Um den Unterrichtsverlauf so gestalten zu können, dass er an die Kompetenzen der Schülerinnen und Schüler anknüpft, sollte die Lehrperson regelmäßig Schülerdokumente analysieren. So kann sie mögliche Schwierigkeiten der Kinder erkennen und auf diese im weiteren Unterrichtsverlauf eingehen.
Im Folgenden können Sie anhand verschiedener Schülerdokumente Ihre Diagnosefähigkeit testen.
Eigenaktivität
Betrachten Sie die Schülerdokumente und beschreiben Sie, was das Kind gut gemacht hat, aber auch in welchem Bereich die Kinder gefördert werden müssen, wenn sie die Fehler systematisch begehen würden.
Hier finden Sie zu jedem Dokument eine mögliche Analyse:
Analyse
Verwandte Themen
Schriftliche Subtraktion
Halbschriftliche Addition
Schriftliche Division
Informative Aufgaben
Um die Rechenwege der Schülerinnen und Schüler besser nachvollziehen zu können, können Sie sich hier mit dem Normalverfahren vertraut machen.
Wenn Sie etwas zum Thema „Schriftliche Addition im Unterricht" erfahren wollen, empfehlen wir Ihnen die Seiten 190ff. „Handbuch für den Mathematikunterricht an Grundschulen" von Wilhelm Schipper (2009).
Materialien zum Thema 'Rechnen auf eigenen Wegen' sowie 'Vom halbschriftlichen zum schriftlichen Rechnen' finden Sie auf der Website des Projekts PIK AS in PIKAS: Haus 5: Individuelles und gemeinsames Lernen.
Material
Aufgabenblatt
Literatur
© Gülay Beyoglu und Jasmin Kötterheinrich für das KIRA-Team