Mathematisches Modellieren ist eine der prozessbezogenen Kompetenzen, die sowohl in den Bildungsstandards als auch im neuen Lehrplan Mathematik NRW gefordert wird. Aber was bedeutet eigentlich Modellieren? Und wie gehen Kinder dabei vor?
Diese Seite versucht einerseits Antworten auf Fragen dieser Art zu geben, lädt andererseits aber auch zur Auseinandersetzung mit dem Modellierungsprozess am Beispiel der Bauernhofaufgabe ein.
"Man braucht 25 Kühe..." - oder?
Eigenaktivität
„Wie viele Kühe bräuchte man, um die ganze Schule eine Woche lang mit Milch zu versorgen?"
Diese Frage haben wir Kindern eines 3./4. Schuljahres gestellt. Eine Gruppe hat ihren Lösungsweg dabei folgendermaßen notiert:

An welchen Stellen würden Sie ähnlich/anders vorgehen? Warum?
Inwiefern wären auch andere Lösungen denkbar?
Was versteht man unter Modellieren?
Mathematisches Modellieren ist eine der prozessbezogenen Kompetenzen, die in den Bildungsstandards und im Lehrplan Mathematik des Landes NRW beschrieben werden. Darin wird unter Modellieren verstanden, Mathematik auf konkrete Aufgabenstellungen aus der eigenen Erfahrungswelt anzuwenden.
Dabei werden Sachsituationen erfasst, in ein mathematisches Modell übertragen und mithilfe mathematischer Kenntnisse und Fertigkeiten bearbeitet. Die gefundene Lösung wird anschließend wieder auf die Sachsituation bezogen. Modellieren stellt damit das „Bindeglied zwischen Umwelt und Mathematik" dar. Im Lehrplan für das Land NRW wird Modellieren wie folgt konkretisiert: Kinder in der Grundschule sollen ...
- Sachsituationen und Sachaufgaben Informationen entnehmen und dabei zwischen relevanten und nicht relevanten Informationen unterscheiden (erfassen).
- Problemstellungen aus Sachsituationen in ein mathematisches Modell übersetzen (z.B. Gleichung, Tabelle, Zeichnung) und mithilfe des Modells zu einer Lösung kommen (lösen).
- ihr Ergebnis wieder auf die Sachsituation beziehen und es auf Plausibilität prüfen (validieren).
- zu gegebenen mathematischen Modellen (z.B. in Form von Gleichungen, Tabellen oder Zeichnungen) passende Problemstellungen finden und im Rahmen von Sachsituationen eigene Fragestellungen entwickeln (zuordnen).
(vgl. MSW NRW 2008, S. 10)
Im Sek I Bereich findet man als Darstellung dieser Teilkompetenzen im Modellierungsprozess häufig einen sogenannten Modellierungskreislauf, der sich sicherlich auch auf den Grundschulunterricht übertragen lässt:
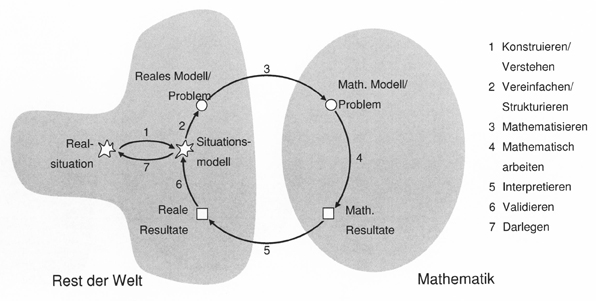
Modellierungskreislauf nach Blum & Leiß (2006)
Vereinfacht gesagt geht es immer darum, zunächst die Aufgabe zu verstehen, dann ein Modell zu erstellen, die Mathematik zu benutzen und schließlich die gefundene Lösung zu erklären. Es sollte an dieser Stelle jedoch hinzugefügt werden, dass tatsächliche Modellierungsprozesse nicht so geradlinig ablaufen, wie dieser Kreislauf sie idealtypisch darstellt.
Eigene Erkundung zum Modellierungsprozess am Beispiel einer Fermi-Aufgabe
Eine Möglichkeit (nicht die einzige!), um das Modellieren bei Kindern besonders gut zu beobachten, stellen Fermi-Aufgaben dar.
Typische Fermi-Aufgaben sind zum Beispiel:
- Wie viele km legt ein Fußballspieler während eines Fußballspiels zurück?
- Wie viele Flugzeuge starten zwischen 12.00 Uhr und 13.00 Uhr von allen Flughäfen in NRW?
- Wie viele Schulen gibt es in Deutschland?
- Wie viele Bücher kann ich in einem Jahr lesen?
- Wie viele Menschen sind in einem 6 km langen Stau?
- Um wie viele Tage wird mein Leben kürzer, wenn ich die Zeit, die ich vor dem Fernseher verbringe, abziehe?
Grundsätzlich sollte man bei einer Verwendung von Fermi-Aufgaben auch immer darüber nachdenken, ob die Fermi-Aufgabe ggf. auch zur Erziehung zur mathematischen Mündigkeit im Sinne des Sachrechnens als Lernziel (vgl. Winter 1994, S. 31 ff.) beitragen kann. So können Fermi-Aufgaben wie z.B.
- Wie viel Müll verbraucht ein Vierpersonenhaushalt pro Woche?,
- Wie viel Wasser verbrauchen wir pro Monat?
dazu beitragen, dass die Kinder über Müllvermeidung oder auch Wassereinsparungen nachdenken.
Eigenaktivität
Suchen Sie sich eine der Fermi-Aufgaben aus und lösen Sie diese.
Beobachten Sie dabei Ihr Vorgehen. Wie passen die von Ihnen unternommenen Einzeltätigkeiten zum Lösen der Aufgabe in den Modellierungskreislauf hinein?
Videoanalyse: Wie bearbeiten Kinder die Bauernhofaufgabe?
Hier können Sie nun beobachten, wie ernsthaft und ausdauernd Kinder des 3. und 4. Schuljahres sich mit der Bauernhofaufgabe beschäftigen.
Eigenaktivität
- Beschreiben Sie anhand des Videos die einzelnen Phasen des Modellierungsprozesses (vgl. Lehrplan Mathematik für das Land NRW und Modellierungskreislauf nach Blum & Leiß 2006), den die Kinder zum Lösen der Aufgabe durchlaufen.
- Warum ist es sinnvoll, Fermi-Aufgaben in Gruppen zu bearbeiten?
- Überlegen Sie, welche prozessbezogenen Kompetenzen bei der Bearbeitung dieser Aufgabe noch zum Tragen kommen.
Anmerkung: Das Video ist relativ lang und der Lösungsprozess der Kinder auch ziemlich komplex. Stoppen Sie das Video am besten zwischendurch oder schauen Sie es sich ggf. sogar mehrmals an.
(Wenn Sie sich das Video anschauen, werden Sie sicherlich auch verstehen, warum wir die Aufgabe „Bauernhofaufgabe" genannt haben.)
Kinder bearbeiten die Bauernhof-Aufgabe (Gruppe B)
Hier finden Sie eine mögliche Beschreibung des Modellierungsprozesses, den die Kinder in dem Video zum Lösen der Aufgabe durchlaufen:Modellierungskreislauf
Weiterführende Aufgabe: Ein anderer Lösungsweg
Gerade bei so offenen Aufgaben wie Fermi-Aufgaben gelangen die Kinder häufig zu ganz unterschiedlichen Lösungen. Schauen Sie sich deshalb an, wie die Kinder aus dem Eingangsbeispiel zu ihrer Lösung „Wir brauchen 25 Kühe ..." gelangt sind.
Eigenaktivität
- Beschreiben Sie auch anhand dieses Videos die einzelnen Phasen des Modellierungsprozesses, den die Kinder hier zum Lösen der Aufgabe durchlaufen.
- Vergleichen Sie insbesondere die verwendeten Zahlenwerte und den Verlauf des Modellierungsprozesses der beiden Gruppen. Wo sehen Sie die Hauptunterschiede?
Kinder bearbeiten die Bauernhof-Aufgabe (Gruppe A)
Nach der Bearbeitung der Bauernhofaufgabe haben die Kinder ihre Lösung und ihren Lösungsweg auf einem Plakat notiert und den anderen Kindern der Klasse präsentiert. Ergebnisse wurden dabei diskutiert, überprüft, verglichen und bewertet. Diese Unterrichtsphase soll mit dem folgenden Video exemplarisch an der Präsentation von Gruppe A demonstriert werden.
Präsentation und Diskussion der Lösung von Gruppe A
Verwandte Themen
Kompetenzen im Mathematikunterricht
Kapitänsaufgaben
Knobelaufgaben
Stützpunktvorstellungen
Zeitungsmathematik
Hier können Sie sich über Sie sich über Fermi-Aufgaben und über ihren Einsatz im Unterricht informieren.
Informations-, Unterrichts- und Fortbildungsmaterial zum Thema 'Prozess- und inhaltsbezogene Kompetenzen' finden Sie auch im PIKAS: Fortbildungsmodul: 'Entdecken, Beschreiben, Begründen' unseres Partnerprojekts PIK AS. Im PIKAS: Fortbildungsmodul: 'Gute Aufgaben' werden außerdem - neben der Förderung von prozessbezogenen Kompetenzen - weitere Charakteristika und unterrichtliche Einsatzmöglichkeiten 'guter Aufgaben' thematisiert und anhand verschiedenster Beispiele illustriert.
Konkrete Unterrichtsideen, wie Sachrechenkompetenzen gefördert werden können, finden sie in primakom: Inhalt: Größen und Messen: Einstieg.
Material
Kindersachbücher zum Thema (nur eine kleine Auswahl):
- Arlon, P. & Obermaier, A.(Hrsg) (2004). Tierlexikon für Kinder. Dorling Kindersley.
- Berger, U. (2004). Was Kinder wissen wollen. Wie macht die Kuh die Milch? Verblüffende Antworten über den Bauernhof. Velber.
- Dreher, K. E. (2004). Der Kinder Brockhaus - Mein erstes Wissen. Auf dem Bauernhof. Brockhaus.
- Stable, M. & Gamlin, L. (2004). Tiere. Wissen für Kinder. Naumann & Göbel.
- Weinberger R. (Hrsg.) (2006). Das Große Tierlexikon. 2000 Arten und ihre Lebensräume. Dorling Kindersley.
- Droop, C.: (2007). Auf dem Bauernhof (Wieso? Weshalb? Warum). Ravensburger Buchverlag.
- Dorling Kindersley (2006). Wissen mit Links: Tiere: Das Schülerlexikon. Dorling Kindersley.
- Wohlert, M. (2004). Was ist was? Bauernhof. Bd. 117. Tessloff.
Internetadressen für Kinder zum Thema (nur eine kleine Auswahl):
www.medienwerkstatt-online.de/lws_wissen/
www.kinder-tierlexikon.de
Weitere Kontexte zum Modellieren:
Bennemann, D., Spiegel, H. & Wenning, A. (1991). Wir verbrauchen zu viel Wasser. Die Grundschulzeitschrift, (42), 11-13 & 60-63. Verfügbar unter: http://math-www.uni-paderborn.de/~hartmut/Eigene_Texte/Wasserverbrauch.pdf [Abruf am: 06.07.2011]
Erichson, Ch. (2003). Von Giganten, Medaillen und einem regen Wurm. Geschichten, mit denen man rechnen muss. Verlag für pädagogische Medien.
Spiegel, H. & Wenning, A. (1991). Lückenhafte Zeitungsmeldungen - Sachmathematik einmal anders. SMP, (19), 114-122. Verfügbar unter: http://math-www.uni-paderborn.de/~hartmut/Eigene_Texte/Lueckenhafte_Zeitungsm.pdf [Abruf am: 06.07.2011]
Literatur