Die schriftliche Division ist in vielen Bundesländern ab dem zweiten Halbjahr des 4. Schuljahres ein Thema des Mathematikunterrichts und wie bei allen anderen schriftlichen Algorithmen treten auch bei diesem Algorithmus spezifische Probleme und Fehler auf.
Im Rahmen ihrer Bachelorarbeit haben sich Bianca Arbogast & Kathrin Dürwald (2011) daher mit typischen Fehlern und deren Entstehung bei der schriftlichen Division auseinandergesetzt, indem sie Arbeitsblätter entworfen und mit diesen eine Studie in fünften Klassen durchgeführt haben. Die Durchführung der Studie fand im ersten Schulhalbjahr statt, weshalb sie nicht in der Grundschule durchgeführt werden konnte.
Auf dieser Seite werden die wesentlichen Erkenntnisse der Arbeit vorgestellt und anhand von Schülerdokumenten illustriert.
Burak rechnet: 1211:7=1613
Der Fünftklässler Burak rechnet die Aufgabe 1211:7 schriftlich. Es scheint ihn wenig zu stören, dass sein Ergebnis 1613 größer ist als der Dividend 1211.
Eigenaktivität
Wie kommt Burak zu seinem Ergebnis 1613? Wie könnte man Burak unterstützen, diesen Fehler in Zukunft zu vermeiden?
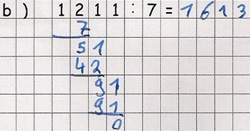
Buraks Lösung
Eine mögliche Erklärung finden Sie hier:
Erklärung Einstiegsaufgabe
Hintergrundwissen zur schriftlichen Division
Der Standardalgorithmus der schriftlichen Division gilt allgemein als der schwierigste der schriftlichen Rechenverfahren, da zahlreiche Anforderungen an die Kinder gestellt werden (vgl. Gerster 1982, S. 164).
Der ohnehin schon umfassende Algorithmus birgt zusätzliche Fehlerquellen, insbesondere des Multiplizierens, des Stellenwertverständnisses und des Subtrahierens (vgl. Padberg & Benz 2011, S. 302 ff.). Zudem erfolgt die Rechenrichtung, anders als bei den anderen schriftlichen Verfahren, von links nach rechts (vgl. Schipper u.a. 2000, S. 118).
Vielleicht ist das ein Grund dafür, dass die Bildungsstandards im Fach Mathematik für den Primarbereich zwar die geläufige Ausführung der schriftlichen Addition, Subtraktion und Multiplikation, sowie die bewusste Anwendung dieser drei Rechenverfahren bei geeigneten Aufgaben als verbindliche Anforderung festlegen, die schriftliche Division aber noch nicht einmal erwähnen (vgl. KMK 2005, S. 9).
„So weit gehen erfreulicherweise die Richtlinien und Lehrpläne der einzelnen Bundesländer allerdings doch nicht" (Padberg & Benz 2011, S. 288). So beschränkt sich z.B. der Lehrplan für das Land NRW darauf, dass die Kinder am Ende der vierten Klasse das schriftliche Divisionsverfahren für einstellige und für wichtige zweistellige Zahlen (wie z.B. 10, 12, 20, 25, 50) an Beispielen erläutern können sollen, eine sichere Ausführung wird allerdings nicht verlangt (vgl. MSW NRW 2008, S. 62).
Einzelne Schritte des schriftlichen Dividierens
Um die im nächsten Abschnitt dargestellten Fehler und Schwierigkeiten bei der schriftlichen Division besser nachvollziehen zu können, sollte man sich über die Komplexität des Algorithmus bewusst sein. Es müssen in der Regel diverse Teilschritte in einer bestimmten Reihenfolge durchlaufen werden, um den Quotienten zu ermitteln. Folgende Schritte sind nach Schipper u.a. (2000, S. 114 ff.) im Allgemeinen notwendig:
1. Überschlagsrechnung
2. Ermitteln des ersten Teildividenden
3. Schätzen der ersten Quotientenziffer
4. Multiplikation
5. Subtraktion
6. Herunterholen der nächsten Ziffer
Im Folgenden werden die oben beschriebenen Schritte anhand eines Beispiels des Fünftklässlers Josef veranschaulicht.
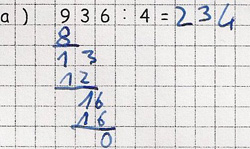
Josef
Überschlagsrechnung: 960:4 = 240
4 passt in die 9 zwei Mal
(Ermitteln des ersten Teildividenden und Schätzen der ersten Quotientenziffer)
2 mal 4 gleich 8
(Multiplikation)
9 minus 8 gleich 1
(Subtraktion)
3 herunterholen
(Herunterholen der nächsten Ziffer)
Diese Schritte werden immer wieder durchlaufen bis alle Ziffern des Dividenden einmal heruntergeholt worden sind.
Da die schriftliche Division in der Grundschule in NRW nur eingeführt wird, aber nicht sicher von den Kindern beherrscht werden muss (vgl. MSW NRW 2008, S. 62), sollte im Sinne der Fortsetzbarkeit in der Sekundarstufe darauf geachtet werden, welche Grundvorstellung der Division (Aufteilen oder Verteilen) bei der Durchführung des Algorithmus angesprochen wird.
Schipper u.a. (2000, S. 115 ff.) verdeutlichen, warum es sinnvoller ist, die Sprechweise und Vorstellung des Aufteilens (im Sinne von "Passen" wie im obigen Beispiel von Josef) für die schriftliche Division zu bevorzugen:
Zum Einen wird das Verfahren des schriftlichen Dividierens in den weiterführenden Schulen auf zwei- und dreistellige Divisoren erweitert. Diese Aufgaben sind kaum mehr im Sinne des Verteilens zu lösen. Zum Anderen profitieren auch schwächere Schüler von dieser Sprechweise.
Manche Kinder beherrschen in der vierten Klasse das kleine 1x1 noch nicht vollständig. Für sie ist das schrittweise Herantasten an den Teildividenden eine große Hilfe, da sie dabei operative Beziehungen ausnutzen können. Wenn zum Beispiel die Aufgabe „34:8" gerechnet werden soll, können die Kinder durch schrittweises Annähern die Lösung finden.
- 3 mal 8 gleich 24 ⇒ 8 passt in die 24 drei Mal;
- 24 + 8 = 32 ⇒ 8 passt in die 32 vier Mal;
- 32 ist das größte Vielfache von 8, welches in 34 enthalten ist, ⇒ also ist die Quotientenziffer 4
(vgl. Schipper u.a. 2000, S. 116 f.)
Typische Fehler
Arbogast & Dürwald (2011) haben im Rahmen ihrer Bachelorarbeit 222 Kindern aus fünften Klassen Aufgaben (im Sinne einer Standortbestimmung) zur schriftlichen Division vorgelegt.
Im Folgenden werden typische Fehler aufgezeigt, die häufig bei der schriftlichen Division auftreten (vgl. Padberg & Benz 2011, S. 302 ff.). Diese werden anhand von Schülerdokumenten aus der oben genannten Bachelorarbeit veranschaulicht.
1. Orientierungsfehler
(Schwierigkeiten beim Zusammenfassen des Teildividenden)
Fehlertyp: Ziffer wird an falscher Stelle heruntergeholt
Beispiel:

Nach der ersten Teildivision hat Nirsine die Differenz „2" mit der heruntergeholten Ziffer 2 zusammengefasst, anstatt die Ziffer 5 herunterzuholen.
Fehlertyp: Zu viele Ziffern zusammengefasst
Beispiel:

Basti hat 93 als Teildividend zusammengefasst, anstatt nur die 9 als Teildividend zu betrachten.
Orientierungsfehler (Kleinschrittiges Suchen des ersten Teildividenden)
Beispiel:
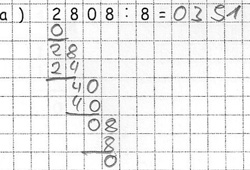
Nina erkennt nicht sofort, welche Ziffern zum ersten Teildividenden zusammengefasst werden müssen. Deshalb teilt sie erst die erste Ziffer (2), sodass der Teilquotient 0 notiert wird. Das Ergebnis ist zwar richtig, jedoch besteht bei diesem Vorgehen das Risiko, die ersten Ziffern des Dividenden falsch abzuschreiben.
Orientierungsfehler (Schwierigkeiten beim Notieren der Zahlen/Ziffern)
Fehlertyp: In der Spalte verrutscht
Beispiel:
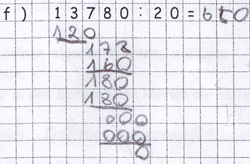
Philipp ist beim Notieren der Differenz „17" eine Spalte nach rechts verrutscht. Die Ziffer 8 hat er richtig heruntergeholt. Allerdings ist er bei der Differenz nach links verrutscht und hat deshalb schon die 0 heruntergeholt. Da nun zwei Teildivisionen untereinander stehen, dividiert er einen Teildividenden davon nicht.
Fehlertyp: Teilquotienten zu viel notiert
Beispiel:

Cedric hat den Teilquotienten „3" zwei Mal notiert.
Fehlertyp: Teilquotient fehlt
Beispiel:
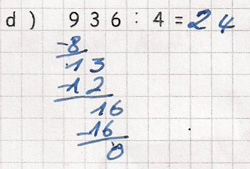
Maria hat den Teilquotienten zur zweiten Teildivision nicht notiert.
2. Fehler beim Überschlagen der Quotientenziffer
Fehlertyp: Quotientenziffer wird zu groß/klein überschlagen
Beispiel:

Wie in der Einstiegsaufgabe wurde auch hier übersehen, dass der Divisor in den zweiten Teildividenden „178" noch einmal mehr hineingepasst hätte. Die Quotientenziffer wurde also zu klein überschlagen. Dadurch wird die nächste Teildivision unnötig schwer und das Ergebnis falsch.
3. Fehler beim Berechnen eines Teilprodukts
Fehlertyp: Schwierigkeiten beim Multiplizieren
Beispiel:

Laura hat den Divisor korrekt überschlagen: „7 passt in die 43 sechs Mal". Jedoch ist die anschließende Multiplikation nicht korrekt („6 mal 7 gleich 41").
4. Fehler bei der Subtraktion
Fehlertyp: Schwierigkeiten beim Subtrahieren
Beispiel:
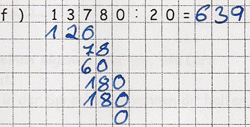
Der Fehler geschah bei der Subtraktion des ersten Teilprodukts.
5. Fehler im Zusammenhang mit Nullen (Schwierigkeiten mit der Zwischennull im Quotienten)
Fehlertyp: Zwischennull im Quotienten wird nicht notiert
Beispiel:

Paul hat das Ergebnis der Teildivision 4:5 nicht im Quotienten notiert. Die Zwischennull im Quotienten fehlt.
Fehler im Zusammenhang mit Nullen (Schwierigkeiten mit der Endnull im Dividenden)
Fehlertyp: Endnull im Dividenden wird nicht dividiert
Beispiel:

Celina hat die Teildivision „0 durch 6" notiert, aber nicht durchgeführt. Daher fehlt die Endnull im Quotienten.
6. Fehler beim Umgang mit dem Rest
Fehlertyp: Rest wird falsch/gar nicht notiert
Beispiel:

Marlene notiert den Rest hinter dem Quotienten nach Einfügen eines Kommas.
Fehleranalyse
Im Folgenden finden Sie Schülerdokumente, in denen mehrere Fehler gleichzeitig auftreten.
Eigenaktivität
Vollziehen Sie nach, wie die Kinder gedacht und gerechnet haben. Welche typischen Fehler sehen Sie in den jeweiligen Kinderdokumenten?
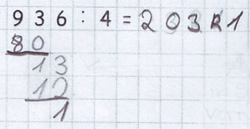
Lars

Chantal
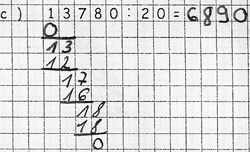
Lelaina
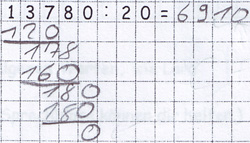
Kurtulus
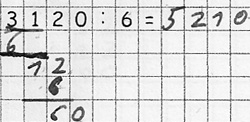
Sören
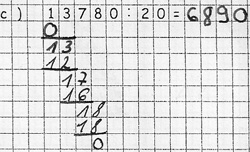
Aylin
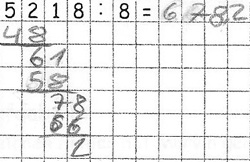
Maren
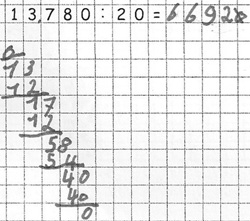
Lucas
Mögliche Interpretationen finden Sie, wenn Sie auf die entsprechenden Namen klicken:
Lars
Chantal
Lelaina
Kurtulus
Sören
Aylin
Maren
Lucas
Schüler erklären Fehler anderer Schüler
Um Fehlvorstellungen vorzubeugen, bietet es sich an, fehlerhafte Rechenwege von anderen (fiktiven) Kindern zu präsentieren und über deren fehlerhafte Rechnungen zu diskutieren (vgl. Padberg & Benz 2011, S. 306).
Derartige Aufgaben stellen einen konkreten Gesprächsanlass über die Funktionsweise des schriftlichen Divisionsalgorithmus dar. In der Studie von Arbogast & Dürwald (2011) wurde Fünftklässlern die fehlerhafte Rechnung des fiktiven Schülers Marvin vorgelegt.

In dieser Aufgabe soll ersichtlich werden, inwieweit Kinder Fehler identifizieren können:
- Erkennen die Kinder den Fehler?
- Wie beschreiben sie ihn?
- Nennen sie die richtige Lösung?
Eigenaktivität
- Analysieren Sie zunächst selbst den Fehler auf dem obigem Arbeitsblatt (Marvins Fehler).
- Bevor Sie weiterlesen: Wie könnten mögliche Antworten von Viert- oder Fünftklässlern lauten?
Eine mögliche Antwort zu Frage 1 finden Sie hier:
Analogie zur Einstiegsaufgabe
Folgende Antworten der Kinder sind besonders interessant:

Maximilians Antwort
Eine mögliche Interpretation dieser Antwort finden Sie hier:
Interpretation Maximilian

Fabians Antwort
Fabian hat erkannt, dass der Teildividend 18 zu klein gewählt wurde und nennt den korrekten Teildividenden und den dazugehörigen Teilquotienten.
Schlussbemerkungen
Die häufigsten Fehler bei der schriftlichen Division sind Fehler im Zusammenhang mit Nullen. Insbesondere die Endnull im Dividenden und die Zwischennull im Quotienten führen häufig zu Fehlern. Zudem gibt es nicht selten Schwierigkeiten beim Finden des ersten Teildividenden.
Außerdem sind das Überschlagen der Quotientenziffer und anschließendes Multiplizieren häufige Fehlerquellen (vgl. Padberg & Benz 2011, S. 302 ff.).
Diese Themen und mögliche Fehlerquellen sollten also gesondert im Unterricht besprochen und thematisiert werden.
Falls Sie sich für weitere Leitideen interessieren, finden Sie hier einige Anregungen:
Weitere Anregungen für den Unterricht
Testen Sie Ihr Wissen zu dem Thema in unserem Kira-Check.
Verwandte Themen
Grundvorstellungen zur Division - Aufteilen und Verteilen
Division mit Rest
Halbschriftliche Division
Schriftliche Addition
Schriftliche Multiplikation
Schriftliche Subtraktion
Falls Sie sich für die Häufigkeiten der jeweiligen Fehlertypen interessieren, die im Rahmen der Bachelorarbeit diagnostiziert wurden, finden Sie diese unter "Häufigkeit der Fehlertypen".
Häufigkeit von Fehlertypen
Materialien zum Thema 'Rechnen auf eigenen Wegen' sowie 'Vom halbschriftlichen zum schriftlichen Rechnen' finden Sie auf der Website des Projekts PIK AS im PIKAS: Fortbildungsmodul: 'Lernen auf eigenen Wegen'.
Material
Arbeitsblätter schriftliche Division
Literatur
© Bianca Arbogast und Kathrin Dürwald für das KIRA-Team