Zur Verdeutlichung der halbschriftlichen Additionsstrategien werden im Folgenden typische Charakteristika anhand von Videos und Schülerdokumenten präsentiert, die Ihnen eine genauere Beobachtung ermöglichen und somit den Einblick in die Vorgehensweisen der Schülerinnen und Schüler erleichtert. Auch werden Ihnen typische Schwierigkeiten bei der halbschriftlichen Addition vorgestellt.
Halbschriftliches Rechnen: Eine Aufgabe - viele Lösungswege
Wir haben Grundschulkindern die Aufgabe 19 + 39 gestellt. Die drei Kinder Timo, Julius und Sabrina haben diese Aufgabe auf sehr verschiede Arten gelöst.
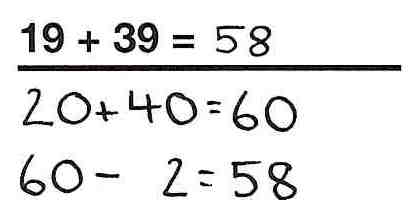
Timo
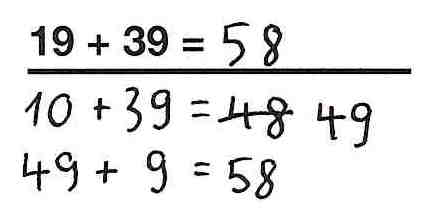
Julius
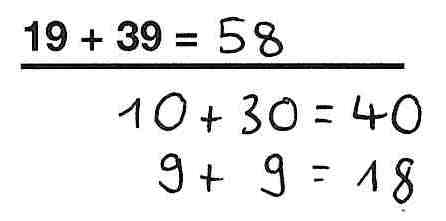
Sabrina
Eigenaktivität
Verstehen Sie, wie die Kinder gerechnet haben? Sie können Ihre Einschätzung überprüfen, indem Sie sich das entsprechende Video ansehen.
Hintergrundwissen: Halbschriftliches Rechnen
Traditionell unterscheiden wir in der Mathematik zwischen drei Hauptmethoden des Rechnens: dem mündlichen, dem halbschriftlichen und dem schriftlichen Rechnen. Als weitere Methode wird heute auch die Berechnung von Aufgaben mithilfe des Taschenrechners hinzu gezählt.
Alle Methoden haben Vor- und Nachteile (vgl. Sundermann & Selter 1995). Schülerinnen und Schüler sollten im Verlauf der Grundschulzeit lernen, sie abhängig von der Aufgabe, aber auch von eigenen Präferenzen flexibel einsetzen zu können (vgl. Selter 1999).
Beim halbschriftlichen Rechnen werden im Kopf durchgeführte Berechnungen durch schriftliche Aufzeichnungen unterstützt. Man spricht daher auch von gestütztem Kopfrechnen (vgl. Radatz u.a. 1998, S. 42).
Das zentrale Kennzeichen des halbschriftlichen Rechnens ist (wie die obigen Beispiele zeigen) das Zerlegen von Aufgaben in leichtere Teilaufgaben. Einzelne Rechenschritte werden notiert, bis am Schluss das Ergebnis ermittelt ist (vgl. Selter 1999, S. 6). Da die Kinder beim halbschriftlichen Rechen mit Zahlenganzheiten und nicht mit Ziffern rechnen, ordnet man es ebenso wie das mündliche Rechnen dem Zahlenrechnen zu.
Das halbschriftliche Rechnen ist im Wesentlichen durch drei spezifische Charakteristika gekennzeichnet, die auch beim Lösen von Additionsaufgaben zu beobachten sind und im Folgenden anhand des Einführungsvideos verdeutlicht werden:
1. Die Rechenwege sind beim halbschriftlichen Rechnen im Gegensatz zu den schriftlichen Algorithmen nicht verbindlich vorgegeben. So sieht man in dem Einstiegsvideo, dass Sabrina und Julius zwei sehr unterschiedliche Zerlegungen der Zahlen nutzen, um das Ergebnis zu ermitteln. (Eine Übersicht zu häufig genutzten Strategien finden Sie im 4. Abschnitt.)
2. Die Notationsweise ist ebenfalls nicht festgelegt. Die Kinder notieren, wie es bei Julius Vorgehen zu sehen ist, nicht unbedingt alle Teilschritte. Das Notieren der Schritte dient lediglich als Merkhilfe. Welche Schritte die Kinder notieren bleibt ihnen selbst überlassen.
Dies führt teilweise dazu, dass das Vorgehen der Kinder nicht immer nachvollziehbar ist und daher erfragt werden muss. (Im 5. Abschnitt finden Sie Beispiele, die verschiedene Notationsweisen zu einer Aufgabe illustrieren.)
3. Welche Lösungsstrategie besonders sinnvoll ist, hängt von der jeweiligen Aufgabe ab. Es ist beispielsweise wenig sinnvoll, 399 +141 in Stellenwerte zu zerlegen. Die Kinder sollen im Unterricht daher vielmehr eine Reihe von Strategien kennenlernen und diese in Abhängigkeit von der gegebenen Aufgabenstellung und der eigenen Präferenz flexibel einsetzen können. Man spricht in diesem Kontext häufig vom Flexiblen Rechnen (vgl. Selter 1999).
Im Einstiegsvideo lässt sich bei Timo erkennen, dass er die Wahl seiner Lösungsstrategie an die Aufgabe anpasst. (Im 6. Abschnitt können Sie anhand von Videos die Vorgehensweisen von Kindern bei verschiedenen Aufgaben genauer betrachten und beobachten, inwiefern die Kinder Strategien flexibel anwenden).
Eigenaktivität
Additionsaufgaben halbschriftlich lösen
- Lösen Sie die Aufgaben 19 + 39 und 399 + 473 halbschriftlich und beschreiben Sie Ihren Rechenweg.
- Welche weiteren Möglichkeiten könnte es geben, um das Ergebnis zu ermitteln? Notieren Sie diese ebenfalls und versuchen Sie, ihren Vorgehensweisen aussagekräftige Namen zu geben.
- Vergleichen Sie Ihre Lösungswege (wenn möglich) mit anderen. Welche Gemeinsamkeiten und Unterschiede entdecken Sie?
Typische Vorgehensweisen bei der halbschriftlichen Addition
Obwohl die Rechenwege beim halbschriftlichen Rechnen nicht vorgeschrieben werden, sind diese keineswegs willkürlich. Wenn die Lösungen der Kinder einen bevorzugten Rechenweg erkennen lassen, so nutzen sie häufig eine der Hauptstrategien des Zahlenrechnens.
Dabei unterscheidet man beim halbschriftlichen Rechnen zwischen einem stellen- oder schrittweisen Vorgehen oder dem Nutzen von Ableitungsstrategien.
Für die Addition ergeben sich, beispielhaft konkretisiert für den Tausenderaum, die folgenden Vorgehensweisen:
1. Stellen extra (auch: Stellenweise)
Beide Summanden werden in Stellenwerte zerlegt:
Z+Z, dann E+E,
oder
E+E, dann Z+Z
Anschließend wird die Gesamtsumme ermittelt.
Beispiel:
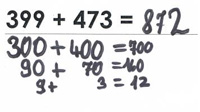
Paul
2. Schrittweise
Ein Summand wird in der Regel in seine Stellenwerte zerlegt:
ZE+Z dann +E
oder
ZE+E dann +Z
Beispiel:
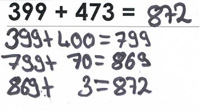
Özge
3. Vereinfachen
Vereinfachungen werden beispielsweise durch das gegensinnige Verändern der beiden Summanden vorgenommen. Demnach rechnen die Kinder unter Ausnutzung von Konstanzgesetzen eine einfachere Aufgabe, die aber das gleiche Ergebnis wie die eigentliche Aufgabe hat.
Beispiel:
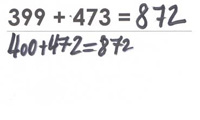
Can
4. Hilfsaufgabe
Die Kinder suchen sich ähnliche Aufgaben, bei denen es leichter ist das Ergebnis zu ermitteln und verändern eine Zahl (oder beide Zahlen) zum vollen Zehner. Dann erfolgt eine nachträgliche Korrektur.
Beispiel:
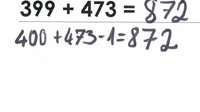
Ali
5. Mischform aus Stellen extra und Schrittweise
Beide Summanden werden zunächst in Stellenwerte zerlegt, die Zehner oder Einer miteinander verknüpft, dann folgt schrittweises Vorgehen:
Bsp.: erst Z+Z, dann E1, dann E2
Beispiel:
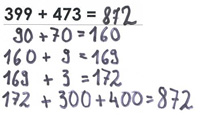
Tim
Typische Vorgehensweisen bei der halbschriftlichen Addition
Eigenaktivität
Zur Vertiefung
- Betrachten Sie erneut Ihre Lösungsstrategien und ordnen Sie Ihre Vorgehensweisen in die obige Tabelle ein. Begründen Sie Ihre Zuordnung.
- Unten finden Sie weitere Kinderdokumente. Ordnen Sie diese den genannten Strategien zu.
AB Zuordnung Hauptstrategien halbschriftliche Addition
Sollten Sie Schwierigkeiten bei der Zuordnung haben, so finden Sie hier einen Vorschlag für die Einordnung der Schülerlösungen:
Lösungen AB Zuordnung Hauptstrategien halbschriftliche Addition
Typische Fehler bei der halbschriftlichen Addition
Beim halbschriftlichen Lösen von Additionsaufgaben treten einige Fehler vermehrt auf. Meseth & Selter (2002, S. 55 ff.) haben in ihrer Studie solche typischen Fehler kategorisiert.
Es ist wichtig zu identifizieren, inwiefern es sich um Merk-, Rechen- oder Verständnisfehler beim halbschriftlichen Addieren handelt. Denn je nach Art des Fehlers und den dahinterliegenden (fehlerhaften) Vorstellungen, müssen diese unterschiedlich aufgearbeitet werden.
Einige Fehler werden in der folgenden Tabelle exemplarisch im Tausenderraum erläutert, um einen ersten Einblick zu gewähren.
1. Verständnisfehler - Anwendung der Umkehroperation
Anstatt zu addieren wird der 2. Summand schrittweise vom 1. Summanden subtrahiert. Das bedeutet, es wird durchgängig die falsche Rechenoperation, nämlich die Umkehroperation, genutzt.
Beispiel:
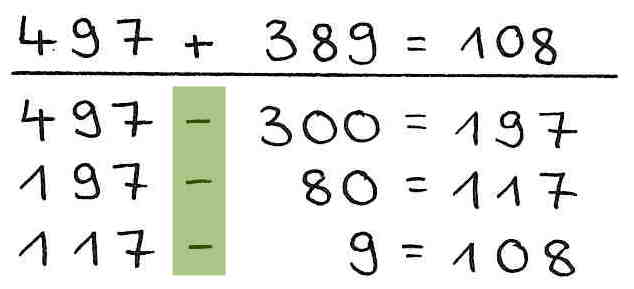
2. Verständnisfehler - fehlerhafte Korrektur der Hilfsaufgabe
Die nachträgliche Korrektur der Hilfsaufgabe findet in die falsche Richtung statt.
Beispiel:
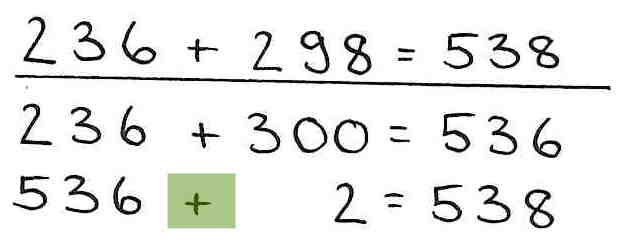
In diesem Beispiel findet die nachträgliche Korrektur der Hilfsaufgabe in die falsche Richtung statt (+ 298 → + 300; - 2).
3. Rechenfehler - ,,Plus-Eins-Fehler''
Zur Ermittlung der Summe der Additionsaufgabe wird ein Zehner überschritten. Analog ist es auch denkbar, dass ein Hunderter überschritten wird. In diesem Zusammenhang ergeben sich oft ,,Plus-Eins-Fehler''.
Beispiel:
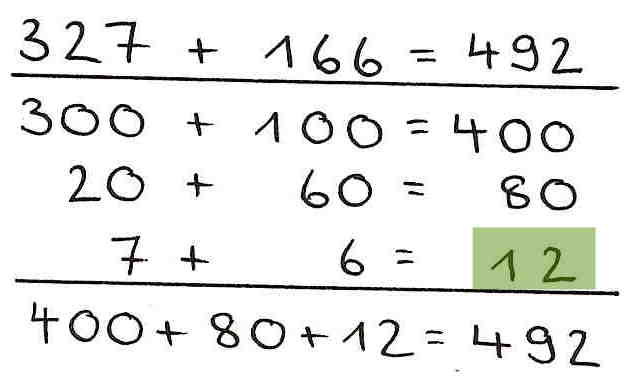
4. Rechenfehler - Vernachlässigung der Stellenwerte
In diesem Beispiel wird bei der zweiten Teilrechnung statt 120 12 als Zwischenergebnis notiert und verrechnet. Der Fehler liegt entweder im Stellenwertverständnis oder einer flüchtigen Notation.
Beispiel:
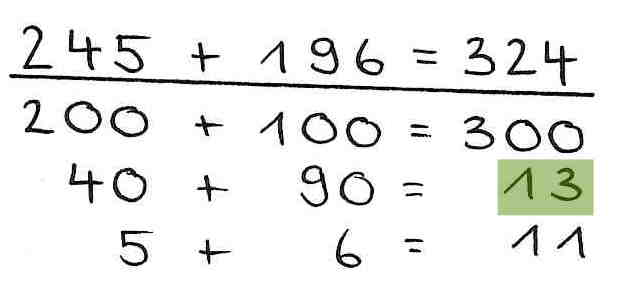
5. Merkfehler
Die Additionsaufgabe wird stellenweise gelöst. Allerdings bleiben Teile des 2. Summanden (hier die Zehner) unberücksichtigt.
Das Vergessen kann ebenfalls die Ermittlung von Zwischenergebnissen betreffen.
Beispiel:
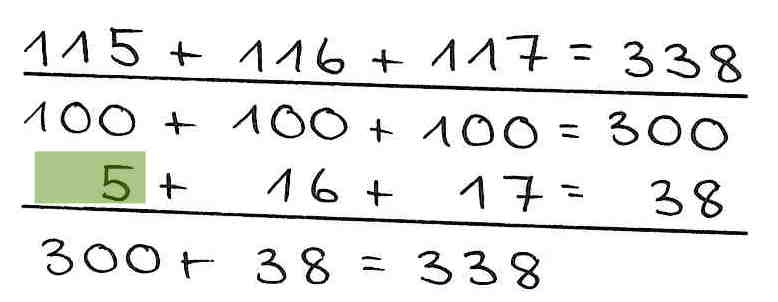
Rechne geschickt: Ein Kind - verschiedene Lösungswege
Wie eingangs erwähnt hängt es von der jeweiligen Aufgabe ab, welche Lösungsstrategie besonders sinnvoll ist. Eine Studie von Selter (1999) zeigt, dass beim halbschriftlichen Rechnen etwa 80% der Kinder die Strategien „Stellen extra" und „Schrittweise" verwenden, auch bei Aufgaben, bei denen die Strategien „Hilfsaufgabe" oder „Vereinfachen" häufig geschickter wären (vgl. Aufgabe: 398 + 241)!
Eigenaktivität
Welche der oben genannten Strategien erweisen sich zur Berechnung der folgenden Aufgaben als besonders sinnvoll? Welche erweisen sich wahrscheinlich als problematisch? Warum?
- 26 + 25 =
- 29 + 12 =
- 15 + 15 =
- 33 + 49 =
- 23 + 45 =
- 19 + 39 =
Eigenaktivität
Betrachten Sie die Videos und überlegen Sie: Welche Rechenstrategie wählt das jeweilige Kind aus? Welche besonderen Vorteile oder Schwierigkeiten ergeben sich aus der Wahl der Strategie?
Julius
Annika
Klaus
Timo
Hier können Sie können Sie sehen, wie die Kinder des zweiten und dritten Schuljahres die verschiedenen Aufgaben im Hunderterraum lösen.
Testen Sie Ihr Wissen zu dem Thema in unserem Kira-Check.
Verwandte Themen
Halbschriftliche Subtraktion
Schriftliche Addition
Addition im Tausenderbuch
Materialien zum Thema 'Rechnen auf eigenen Wegen' sowie 'Vom halbschriftlichen zum schriftlichen Rechnen' finden Sie auf der Website des Projekts PIK AS im PIKAS: Fortbildungsmodul: 'Lernen auf eigenen Wegen'.
Die meisten Erwachsenen kennen aus der Schule entweder nur die schriftlichen Rechenverfahren oder nutzen im Alltag intuitiv halbschriftliche Vorgehensweisen. Als Lehrperson mit dem Fach Mathematik sollten Sie allerdings die große Vielfalt halbschriftlicher Rechenverfahren kennen und im Unterricht mit Blick auf die individuellen Vorlieben der Lernenden die eine oder andere Strategie thematisieren. Das stellt fachfremd Unterrichtende vor eine große Herausforderung, da sie selbst in ihrer damaligen Schulzeit nur auf die schriftlichen Rechenverfahren eingetrimmt wurden.
Besuchen Sie deshalb die Homepage des Projekts PriMakom („Primarstufe Mathematik kompakt“). Dabei handelt es sich in erster Linie um eine Selbstlernplattform für Lehrerinnen und Lehrer, die Mathematik fachfremd unterrichten und sich somit fachdidaktische Kenntnisse in kompakter Form aneignen möchten. Dort erhalten Sie kompakte Hintergrundinformationen, sowie unterrichtspraktische Hinweise zu den halbschriftlichen Rechenstrategien in primakom: Inhalte: Zahlen und Operationen: Halbschriftliches Rechnen: Einstieg.
Literatur
