Kinder bringen nicht nur Vorwissen mit, wenn sie als Erstklässler in die Schule kommen. Auch wenn ab Mitte des zweiten Schuljahres Multiplikation und Division thematisiert werden, können die Kinder häufig schon mehr als erwartet. Deshalb gilt es zu Beginn der Einführung mithilfe geeigneter Aufgaben die Standorte der Kinder zu bestimmen, um an die Vorkenntnisse anknüpfen und diese ausbauen zu können.
Auf dieser Seite zeigen wir Ihnen, wie vielfältig und bemerkenswert die Lösungsstrategien der Kinder sein können, aber auch wie sich diese informellen Vorgehensweisen im Laufe der Zeit weiterentwickeln.
Wie viele Riegel bekommt jedes Kind?
Diese Divisionsaufgabe (Hengartner & Röthlisberger, 1999, S. 39) haben wir Kindern des zweiten Schuljahres noch vor der Einführung der Division vorgelegt.

(Hengartner & Röthlisberger, 1999, S. 39)
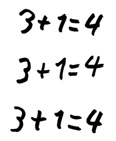
Karolas Lösung

Janinas Lösung
Welche Kompetenzen zeigen Karola und Janina bei der Lösung dieser Aufgabe?
Hintergrundwissen zum Vorwissen zur Multiplikation und Division
Geeignete Aufgaben finden
Bei der Erhebung des Vorwissens von Kindern sollten die verwendeten Aufgaben in etwa das bevorstehende Unterrichtsspektrum umfassen (vgl. Hengartner & Röthlisberger 1999, S. 36). Neben offenen Aufgaben wie z.B. „Schreibe alle Malaufgaben auf, die du schon kennst" bieten sich des weiteren Kontexte an, die an die Lebenswirklichkeit der Kinder anknüpfen, sodass deren Vorwissen und informellen Strategien direkt aktiviert wird.
Will man das Vorwissen ohne zu großen Zeitaufwand in einer ganzen Klasse (schriftlich) erheben, ist es außerdem wichtig, dass die Aufgaben möglichst selbsterklärend sind. Hengartner & Röthlisberger (1999) haben gemeinsam mit Studentinnen und Studenten den Versuch unternommen, solche kontextgebundenen Aufgaben zu entwickeln und damit die Standorte von Kindern zu bestimmen.
Dabei ist ein Satz an Bildaufgaben entstanden, so wie die Aufgabe im Eingangsbeispiel, die die Multiplikation bzw. Division nahelegen, die aber auch auf andere, informelle Weise gelöst werden können.

(Hengartner & Röthlisberger, 1999, S. 39)
Besonders charakteristisch für die Aufgaben ist, dass die Bilder, anders als „gewöhnliche" Text- und Bildaufgaben, Zählvorgänge erschweren und eine strukturierte Anzahlerfassung begünstigen (ebd.).
So sind in der obigen Abbildung rechts beispielsweise nicht alle Fenster sichtbar, sodass es nahezu unvermeidbar ist, die Struktur der Fensteranordnung zu erkennen und zu nutzen, was für die Multiplikation und Division eine wichtige Kompetenz darstellt.
Wichtig ist, dass die Lehrperson die informellen Strategien der Kinder einzuordnen und zu schätzen weiß. Denn primäres Ziel einer solchen Standortbestimmung ist es nicht, zu überprüfen, was die Kinder in Sachen Multiplikation noch nicht können, sondern welche Voraussetzungen und welches Wissen über die Multiplikation (Division) sie schon mitbringen.
Dazu gehört auch, dass die Lehrkraft versuchen muss, das Unbewusste bewusst zu machen, um einen möglichst umfassenden Eindruck über die informellen Fähigkeiten und Vorerfahrungen zur Multiplikation und Division des Kindes zu bekommen (vgl. hierzu: Interviews durchführen).
Informelle Lösungsstrategien
Multiplikation
Die Vorkenntnisse zur Multiplikation standen bereits im Fokus vieler Studien (Padberg & Benz 2011, S. 124 f.). Wenngleich die Vielfalt der in den Studien genannten Strategien sehr hoch ist, so lassen sich doch einige „typische" Lösungsstrategien festhalten (ebd., S. 126 f.). Einige dieser Strategien sollen im Folgenden illustriert werden:
1. Lösungsstrategie: Direktes Modellieren/vollständiges Auszählen
Beispiel:
Meike
2. Lösungsstrategie: Rhythmisches Zählen in gleichgroßen Teilabschnitten (mit oder ohne Material)
z.B. 1, 2, 3, 4, 5, 6, ..., 31, 32, 33 für 13 · 3
Beispiel:
Justus
3. Lösungsstrategie: Benutzung von Zahlenfolgen (mit oder ohne Material)
z.B. 3, 6, 9, 12
Beispiel:
Meike
4. Lösungsstrategie: Wiederholstes Addieren gleicher Summanden
z.B. 3 + 3 + 3 + 3
Beispiel:
Melinda
5. Lösungsstrategie: Multiplikative Rechnungen
z.B. 4 · 4
Beispiel:
Justus
Division
Teilweise abhängig von den Aspekten des Verteilens und Aufteilens (vgl. Aufteilen und Verteilen) lassen sich auch bei der Division noch vor der systematischen Einführung bestimmte Lösungsstrategien bei Kindern beobachten (Padberg & Benz 2011, S. 151 f.):
1. Lösungsstrategie: Einzelnes Verteilen/Vollständiges Auszählen
Beispiel:
Janina
2. Lösungsstrategie: Wiederholte Addition (bei Verteilaufgaben nur in Verbindung mit Schätzstrategien)
Beispiel:
Zarah
3. Lösungsstrategie: Wiederholte Subtraktion (vorwärts oder rückwärts, bei Verteilaufgaben nur in Verbindung mit Schätzstrategien)
Beispiel:
Meike
4. Lösungsstrategie: Rückgriff auf Multiplikation
Zur Zeit liegt kein Video vor.
Analyse von Schülerdokumenten und Videos
Wir haben die Aufgaben in Anlehnung an Hengartner & Röthlisberger (1999) und Gloor & Peter (1999) neu aufbereitet und Kindern des zweiten Schuljahres im klinischen Interview vorgelegt, noch bevor die Multiplikation und Division im Unterricht thematisiert wurde. Einige der so entstandenen Videos konnten Sie bereits weiter oben betrachten.
Während dort aber bestimmte Vorgehensweisen illustriert wurden, gilt es nun, dass Sie selbst einmal versuchen, die Vorkenntnisse der Kinder einzuordnen. Bedenken Sie dabei, dass die Kinder die Aufgaben noch längst nicht lösen können müssen!
Heterogenität von Lösungswegen
In den folgenden Videos sehen Sie verschiedene Kinderlösungen zu einer Aufgabe.
- Welche der oben genannten informellen Strategien lassen sich erkennen?
- Inwiefern nutzen die Kinder bereits Fachsprache der Multiplikation (z.B. "mal", "Reihe", ...)?
- Welche Gemeinsamkeiten und welche Unterschiede sehen Sie in den Vorgehensweisen und dem Vorwissen der drei Kinder?
Sinnhaftigkeit von Lösungswegen trotz falscher Ergebnisse
Im Folgenden finden Sie Kinderlösungen zu verschiedenen Aufgaben, die nicht immer zum korrekten Ergebnis geführt haben.
- Wie können Sie die entstandenen Fehler erklären?
- Welche Kompetenzen können Sie dennoch erkennen?
Janina
Karola
Maurits
Lernentwicklungen
Manchen der Kinder, die wir bereits im Herbst interviewt haben, haben wir die gleichen Aufgaben (entnommen aus: Hengartner & Röthlisberger 1999) ein halbes Jahr später erneut vorgelegt, als die Multiplikation gerade seit einigen Wochen im Unterricht behandelt wurde.
Hier sehen Sie nun Videoausschnitte, in denen das Vorgehen von Laura vor der Einführung der Multiplikation und während der unterrichtlichen Behandlung zu sehen ist.
- Beschreiben Sie die Lernentwicklung des Kindes.
- Wie würden Sie sich die hier gemachten Beobachtungen zu Nutzen machen, um das Kind individuell zu fördern?

(Hengartner & Röthlisberger, 1999, S. 39)
Vor der unterrichtlichen Behandlung der Multiplikation:
Während der unterrichtlichen Behandlung der Multiplikation:

(Hengartner & Röthlisberger, 1999, S. 39)
Vor der unterrichtlichen Behandlung der Multiplikation:
Während der unterrichtlichen Behandlung der Multiplikation:
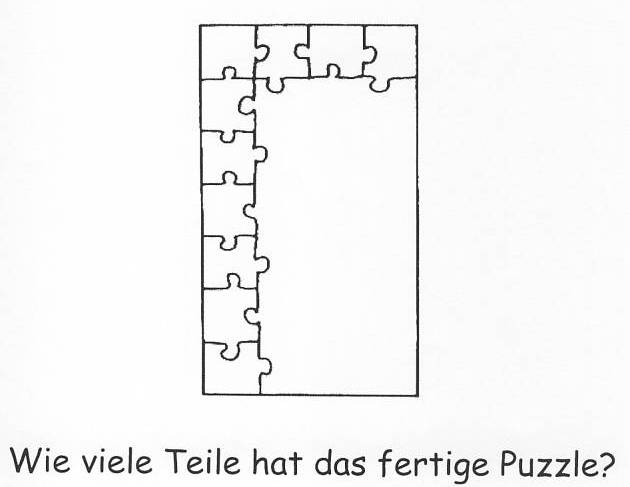
(Hengartner & Röthlisberger, 1999, S. 39)
Vor der unterrichtlichen Behandlung der Multiplikation:
Während der unterrichtlichen Behandlung der Multiplikation:

(Hengartner & Röthlisberger, 1999, S. 40)
Vor der unterrichtlichen Behandlung der Multiplikation:
Während der unterrichtlichen Behandlung der Multiplikation:
Testen Sie Ihr Wissen zu dem Thema in unserem Kira-Check.
Verwandte Themen
Interviews durchführen
Grundvorstellungen zur Division - Aufteilen und Verteilen
Rechenfähigkeit am Beispiel Schachtelaufgaben
Orientierung im Zahlenraum bis 100
Auf der Website des Projekts PIK AS finden Sie im PIKAS: Fortbildungsmodul: 'Lernstände wahrnehmen' weitere Materialien zum Thema 'Standortbestimmungen'.
Der Aufbau mentaler Vorstellungen von den Operationen und das Erkennen von Zusammenhängen zwischen einzelnen Aufgaben, kann durch Materialhandlungen deutlich unterstützt werden und führt langfristig zu einem größeren Lernerfolg. Wie dies am Beispiel des kleinen 1x1 geschehen kann, erfahren Sie in primakom: Übergreifendes – Prinzipien – Gestütztes Üben – Einstieg.
Literatur