Diese Seite bietet Ihnen Einsicht in die Vorgehensweisen von Erstklässlern bei der Bearbeitung von Additions- und Subtraktionsaufgaben. Vollziehen Sie die verschiedenen Strategien der Kinder beim Lösen der Aufgaben nach und verdeutlichen Sie sich die Vielfalt an Vorgehensweisen, welche dieses Themengebiet mit sich bringt.
Davids Rechentrick bei der Aufgabe 5+6
In einem Interview wurden dem Erstklässler David verschiedene Additionsaufgaben gestellt. Es entstand folgender Dialog:
I: Und was sind 5 und 6?
D: (Überlegt wenige Sekunden) 11
I: Woher weißt du das?
D: Wenn der andere auch 6 wäre, dann wären es ja 12. Und einer weniger macht 11.
Hintergrundwissen zum additiven und subtraktiven Rechnen im 20er-Raum
Die Addition und Subtraktion sind in der Regel die ersten Rechenarten, mit denen sich Kinder - auch schon vor Schulbeginn - auseinandersetzen (vgl. z.B. Spiegel 1992, Selter 1995, Deutscher 2011).
Im ersten Schuljahr werden diese beiden Operationen vor dem Hintergrund der zum Teil weitreichenden Vorerfahrungen der Kinder als Hauptthemengebiet des Mathematikunterrichts behandelt. Meist werden die beiden Grundrechenarten aufgrund ihrer engen Beziehung als Operation (Addition) und Umkehroperation (Subtraktion) parallel eingeführt.
Somit werden die Schülerinnen und Schüler auf den Zusammenhang der Operationen aufmerksam gemacht und zum reversiblen Denken angeregt (vgl. Hasemann 2007, S. 92; Padberg & Benz 2011, S. 114).
Additions- und Subtraktionsaufgaben werden im Anfangsunterricht auf ganz verschiedene Weisen von Kindern bearbeitet. Man kann dabei zwischen drei Hauptstrategien unterscheiden: dem 1) Zählen , dem 2) Rechnen und dem 3) (Auswendig-)Wissen (vgl. Padberg & Benz 2011, S. 88-101 sowie S. 111-117).
Ziel des Unterrichts ist es, bei den Kindern zunächst ein Verständnis der Rechenoperationen aufzubauen, um anschließend effiziente Lösungsstrategien gemeinsam zu entwickeln, die bis zu einer Automatisierung der Aufgaben im Zwanzigerraum führen. Der Aufbau eines adäquaten Zahl- und Operationsverständnis steht hierbei im Mittelpunkt.
Gerade in der Einführungsphase werden daher Anschauungsmaterialien verwendet, die die Schülerinnen und Schüler bei der Bearbeitung von Rechenaufgaben nutzen können um solide Zahl- und Operationsvorstellungen aufzubauen (Was heißt "plus"? Was heißt "minus"? Was passiert mit der Summe, wenn ein Summand um Eins erhöht wird? ...).
Die Anschauungsmaterialien (wie z.B. Plättchen oder das Zwanzigerfeld) machen es den Kindern möglich, an konkreten Objekten zu handeln oder sich die Rechnung anhand einer bildlichen Darstellung zu verdeutlichen (vgl. Hasemann 2007, S. 94). Somit können sich die Schülerinnen und Schüler die Anzahlen und Operationen veranschaulichen und diese zunehmend verinnerlichen (vgl. ebd., S. 94).
Nur wenn die Schülerinnen und Schüler über hinreichende verständnisbasierte Sicherheit in der Ausführung der Operationen im Zahlenraum bis 20 verfügen, macht es Sinn, den Zahlenraum zu erweitern.
Eigene Erkundungen: Das Operieren mit Zahlen aus Sicht der Kinder
Um die Vorgehensweisen und Schwierigkeiten der Kinder bei der Addition und Subtraktion besser nachvollziehen zu können, eignet es sich, selbst einmal in einem fremden Zahlensystem zu rechnen.
Stellen Sie sich folgendes Zahlensystem vor:
Die Ziffern 0-9 werden durch die Buchstaben a-j ersetzt. Die Zahl 0 heißt in diesem Zahlensystem daher a, die 1 nun b, die 2 c usw..
Versuchen Sie die folgenden Additions- und Subtraktionsaufgaben zu lösen, ohne auf das Ihnen bekannte Zahlensystem zurückzugreifen:
c + b =
d + e =
f - c =
i - e =
Reflektieren Sie Ihr Vorgehen: Welche Strategien haben Sie verwendet, um das Ergebnis zu ermitteln? Bei welchen Aufgaben konnten Sie das Ergebnis leicht bestimmen, bei welchen fiel dies schwerer und warum?
Bei diesem Experiment kann auch geübten Rechnern deutlich werden, was Kinder beim Lösen von Additions- und Subtraktionsaufgaben leisten, und welche Gedankengänge vollzogen werden müssen, sofern sie mit Zahlen und den entsprechenden Operationen erst wenig vertraut sind.
Addition unter Zuhilfenahme von Plättchen
Steht Kindern bei der Bearbeitung von Additionsaufgaben Material zur Verfügung (man spricht dann auch vom gestützten Üben), können sie konkret an diesem handeln. Sie können die Operation des Hinzufügens (als eine Grundvorstellung der Addition) hieran ausführen und dabei die Objekte und deren Anzahlen im Blick behalten. Ob und in welcher Weise die Kinder das Material nutzen, kann sehr unterschiedlich sein.
Eigenaktivität
Schauen Sie sich folgendes Video an und beobachten Sie, wie die Kinder die Additionsaufgaben lösen:
- (Inwiefern) Nutzen die Kinder die Veranschaulichung der Aufgaben durch Plättchen?
- Welche Möglichkeiten ergeben sich für die Kinder durch das Material?
Das Rechnen mit Plättchen stellt für viele Kinder eine Hilfestellung bei der Erfassung und Durchführung von Operationen dar. Die Spannbreite der Nutzungsweisen des Materials ist dabei sehr groß. Sie reicht vom vollständigen Abzählen der Plättchen bis zum geschickten Umlegen dieser in eine übersichtlichere Rechnung bzw. Zahldarstellung.
Für den Anfangsunterricht eignen sich Plättchen um erste Rechnungen darzustellen. Aufgrund der Gefahr, dass sich durch das alleinige Arbeiten mit Plättchen das zählende Rechnen verfestigen kann, sollten Kinder nicht zu lange bei diesem Anschauungsmaterial verweilen, sondern Material verwenden, das die ‚Kraft der Fünf' ausnutzt (Rechenrahmen, Zwanzigerfeld etc.).
Vorgehensweisen bei der (formalen) Addition
Auch ohne Zuhilfenahme von Material können Additionsaufgaben auf ganz verschiedene Weisen gelöst werden. Kinder greifen hierbei auf ihre Erfahrungen mit Zahlen und Operationen zurück und gehen aufgrund ihrer Vorkenntnisse der einen oder anderen Lösungsstrategie nach. Für Lehrerinnen und Lehrer ist es wichtig, mögliche Lösungsstrategien zu kennen, um Kinder in ihrem Vorgehen zu verstehen und ggf. gezielte Unterstützung anbieten zu können.
Eigenaktivität
Ordnen Sie die Vorgehensweisen der Kinder den einzelnen Strategien zu. Informieren Sie sich zuvor, wenn nötig, über die drei Hauptstrategien (und ihre Unterstrategien) "Zählen", "Rechnen" und "Wissen" aus Kapitel 2.
Okan
Marie
Sören
Maurice
Hier sehen Sie eine mögliche Zuordnung.
Vorgehensweisen bei der kontextgebundenen Subtraktion
Um Kindern einen leichteren Zugang zu einer Rechnung zu ermöglichen, können Aufgaben in einen Sachkontext eingebettet werden. Dadurch können die Kinder sich die Situation und damit auch die Operation konkret vorstellen und gedanklich durchführen. Bei Sachaufgaben zur Addition wird das Hinzufügen durch den Sachbezug verdeutlicht, das Wegnehmen steht im Zentrum von Sachaufgaben zur Subtraktion, wobei diese auch durch die Strategie des Ergänzens gelöst werden können (vgl. hierzu: Halbschriftliche Subtraktion).
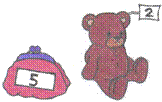
„Du hast 5 Euro und du kaufst dir einen Teddy für 2 Euro. Wie viele Euro hast du dann noch übrig?"
(Die Sachsituation wurde den Kindern hierbei zusätzlich anhand der Abbildung verdeutlicht)
Eigenaktivität
Schauen Sie sich die Videos an und beobachten Sie, welche Strategien die Schülerinnen und Schüler verwenden. Informieren Sie sich zuvor, wenn nötig, über die drei Hauptstrategien (und ihre Unterstrategien) "Zählen", "Rechnen" und "Wissen" aus Kapitel 2.
Gabriel
Lila
Max
Hier können Sie überprüfen, welchen Strategien die Kinder nachgehen.
Testen Sie Ihr Wissen zu dem Thema in unserem Kira-Check.
Verwandte Themen
Halbschriftliche Addition
Halbschriftliche Subtraktion
Bildliche Darstellungen
Im PIKAS Fortbildungsmodul: 'Rechenschwierigkeiten' finden Sie Informationen zum Thema. Im PIKAS: Unterrichtsmodul: 'Zahlen und Operationen: Addition üben' sowie im PIKAS: 'Unterrichtmodul: 'Zahlen und Operationen: Blitzrechnen', finden Sie Materialien zur Automatisierung dieser wichtigen Basiskompetenzen.
Ein zentraler Inhalt im Mathematikunterricht der Grundschule ist, dass die Kinder alle vier Grundrechenarten beherrschen und ausführen können. Um tragfähige Vorstellungen aufzubauen, benötigen die Kinder verschiedene Teilkompetenzen. Am Beispiel der Subtraktion wird in primakom: Inhalte – Zahlen und Operationen – Operationsverständnis aufbauen – Einstieg dargestellt, wie ein Operationsverständnis aufgebaut werden kann.
Literatur