Aufgaben zur Wahrscheinlichkeit bieten vielfältige Möglichkeiten, prozessbezogene Kompetenzen anzubahnen. Arbeitsaufträge wie „Begründe deine Entscheidung!" und „Warum kannst du dir sicher oder nicht sicher sein, dass deine Entscheidung stimmt?", fordern Kinder dazu auf, ihre Entscheidungen zu prüfen und mathematisch zu begründen.
Im Folgenden bekommen Sie die Möglichkeit, eigenständig Wahrscheinlichkeiten im Zufallsexperiment einzuschätzen und zu begründen und ihre Erkenntnisse mit Schülerlösungen zu vergleichen. Abschließend sollen die Begründungen im Hinblick auf die individuellen Vorstellungen des Wahrscheinlichkeitsbegriffs geprüft werden.
Zur Darstellung der Ergebnisse werden Schülerdokumente aus einem 4. Schuljahr verwendet, die im Rahmen der Masterarbeit von Anne Tente (2012) entstanden sind.
Wer hat aus welchem Säckchen gezogen?

Eigenaktivität
- Lösen Sie die Aufgabe und begründen Sie Ihre Entscheidung. Wichtig: Das Begründen mit höher mathematischen Überlegungen ist erlaubt, zusätzlich sollten Sie dann aber eine weitere grundschulgemäße Begründung formulieren.
- Reflektieren Sie Ihre Begründungen: Sind Ihre Begründungen aussagekräftig? Notieren Sie die wichtigsten Merkmale Ihrer Begründung. Vergleichen Sie Ihre Begründungen mit Janoschs Erläuterung (siehe unter Aufgabe 3).
- Diskutieren Sie Ihre Begründungen ggf. mit Ihren Kommilitoninnen und Kommilitonen bzw. Kolleginnen und Kollegen. Vergleichen Sie Ihre Merkmale und versuchen Sie, Gemeinsamkeiten und Unterschiede herauszuarbeiten. Beziehen Sie auch Janoschs Begründung mit ein.
Janosch: "Ich glaub Paul hat aus dem [tippt mit dem Finger auf das Säckchen mit 20 roten und 80 blauen Perlen] [...] weil da sind mehr Blaue drin."
Hintergrundwissen
Das Vergleichen von Wahrscheinlichkeiten für Ereignisse in Zufallsexperimenten zählt zu den inhaltsbezogenen Kompetenzen des Lehrplans von NRW (2008). Am Ende der vierten Klasse sollen die Schülerinnen und Schüler laut diesem Lehrplan Wahrscheinlichkeiten von einfachen Ereignissen sicher beschreiben (sicher, wahrscheinlich, unmöglich, immer, häufig, selten, nie) (vgl. MSW NRW 2008, S. 66) können.
Im folgenden Abschnitt wird zunächst die mathematische Bedeutung des Wahrscheinlichkeitsbegriffs verschiedenen Schülervorstellungen gegenübergestellt. Im Anschluss werden im Überblick die Wahrscheinlichkeiten im Urnenmodell bestimmt, zugeordnet und begründet.
Wahrscheinlichkeitsbegriff
Mathematische Begriffserklärung
In der Stochastik kommt dem Wahrscheinlichkeitsbegriff eine andere Bedeutung zu als im Alltagsgebrauch (vgl. Eichler & Vogel 2009, S. 171). Neubert (2009) erklärt, dass der Begriff in der Stochastik immer im Zusammenhang mit Ereignissen erfolgt, die unter bestimmten Bedingungen eintreten können, aber nicht eintreten müssen, bei denen also mehrere Ausgänge möglich sind. Solche Ereignisse werden als zufällige Ereignisse bezeichnet.
Die Wahrscheinlichkeit bezeichnet somit das Maß an Sicherheit für das Eintreten von Ereignissen bei Zufallsversuchen (vgl. Neubert 2009). Die Chance für das Eintreten eines Ereignisses kann durch einen Wert zwischen 0 und 1 angegeben werden.
Der Wert 1 steht dabei für ein „sicheres Ergebnis", das auf jeden Fall eintreten wird. Der Wert 0 bezeichnet hingegen ein „unmögliches Ergebnis", das auf keinen Fall eintreten wird. Der Begriff „wahrscheinlich" deckt alle Fälle ab, die zwischen diesen beiden Extremen liegen (vgl. Hahn, Kahnt & Maurer 2009, S. 10 ff.).
Vergleich mit Schülervorstellungen
Wahrscheinlichkeiten: Interviewleitfaden
In einer Interview-Studie (vgl. Tente 2012) sind die Kinder einer vierten Klasse in Einzelinterviews aufgefordert worden, den Begriff „wahrscheinlich" zu erläutern. In ihren Erklärungen traten häufig alltagsbezogene Begriffe und Erklärungen auf:
Henning: "Vielleicht, dass wahrscheinlich, dass man wahrscheinlich diese Perlen, dass man wahrscheinlich diese Farbe zieht. Joa (...) dass es wahrscheinlich ist, dass man nicht die Blaue zieht zum Beispiel, wenn man jetzt nur in ein Säckchen mit nur Roten."
Marvin: "Also em ich versteh darunter, also em dass man also so wie schätzen, also wahrscheinlich - em - sind da - em - sind das Hundertsechzig oder so. Wenn man sich nicht sicher ist."
Lena: "Also ähm, so genau weiß ich das jetzt nicht, aber wahrscheinlich bedeutet eigentlich, dass em man so zu sagen ‚vielleicht‘ glaub ich. Also das man mh, wahrscheinlich jetzt sag ich mal (...) [zieht die Schultern hoch] Ich mach mal ein Beispiel. [...] Wenn man - em - man Geburtstag oder so hat und ne Party machen will (lacht) dann kann man das vielleicht, wenn man lieb war, auch wahrscheinlich bekommen - also - also so ein gutes Beispiel ist das nicht, aber ein anderes fällt mir nicht ein."
Janosch: "JA, so wie ne Vermutung, also wahrscheinlich ergibt das das."
Fabian: "Wahrscheinlich, em (...) weil vielleicht em - das em - also weil em wahrscheinlich halt so ein Wort ist em das - dass wahrscheinlich in der Mathematik, vielleicht wenn em - wenn ein äh - wenn ein äh Mathematiker sagt em dann würd - in der späteren Zeit wird dies und das und das passieren. Und dann und dann sagt er ja wahrscheinlich, weil er das ja nicht richtig voraussagen kann."
Nina: "Äh, also das es -äh (stöhnt) [...] mh, dass das em, dass ich das (...) bestimmt ziehe."
Im Vergleich zu der oben dargestellten Begriffsklärung weichen die alltagsbezogenen Synonyme sowie Erklärungen der Kinder insofern ab, als dass die Wahrscheinlichkeit meist als etwas Mögliches dargestellt wird, was aber nicht fester bestimmt werden kann. Die Kinder erklären den Begriff eher als eine vage Vermutung oder Schätzung.
Weitere Hinweise zur näheren Analyse und Bewertung der dargestellten Schülerdokumente erhalten Sie hier:
Wahrscheinlichkeiten: Bewertung der Schülerlösungen
Ob die Grundvorstellungen der Kinder ihre Begründung der Zuordnung der Wahrscheinlichkeit aus der Einstiegsaufgabe beeinflusst, soll in der Analyseaufgabe (vgl. Abschnitt 3) näher untersucht werden.
Wahrscheinlichkeiten am Urnenmodell bestimmen, zuordnen und begründen
Im Hinblick auf die Einstiegsaufgabe wird zunächst das Urnenmodell in Kürze vorgestellt. Des Weiteren wird ein Zugang zur Wahrscheinlichkeit aufgezeigt und die Möglichkeiten des Argumentierens im Kontext der Wahrscheinlichkeitsrechnung dargelegt, bevor abschließend mögliche Begründungsebenen für die Zuordnung von Wahrscheinlichkeiten dargestellt werden.
Urnenmodell
Das Urnenmodell ist ein Oberbegriff für eine Vielzahl an Aufgaben, in denen grundsätzlich Gegenstände gleicher Form aus einem Gefäß gezogen werden. Diese Gegenstände werden immer zufällig gezogen (vgl. Dehn, Mayer, Weisbach & Neubert 2007, S. 34). Somit dient es als ein Modell für verschiedene Zufallsgeneratoren. Neben vielfältigen Situationen kann das Urnenmodell auch auf verschiedene Aufgabenstellungen angewandt werden.
In der Interview-Studie ist den Kindern unter anderem die oben dargestellte Einstiegsaufgabe gegeben worden. Sie sind aufgefordert worden, die zwei verschiedenen Ziehungen den zwei verschiedenen Urneninhalten zuordnen und ihre Entscheidungen zu begründen. Wie Wahrscheinlichkeiten bestimmt werden können, wird im Folgenden kurz aufgezeigt.
Wahrscheinlichkeiten bestimmen
Der Zugang zur Wahrscheinlichkeit ist prinzipiell auf zwei verschiedenen Wegen denkbar: Zum einen über den empirisch-statistischen und zum anderen über den klassisch-kombinatorischen Weg (vgl. Dehn, et al. 2007, S. 35).
Bei der Einstiegsaufgabe ist der empirisch-statistische Zugang von Bedeutung:
Beim empirisch-statistischen Zugang wird ein Zufallsexperiment, hier am Beispiel des Urnenmodells, in mehreren Durchgängen wiederholt. Schließlich kann anhand einer Serie von Experimenten die Wahrscheinlichkeit eines Ereignisses abgeschätzt werden (vgl. Dehn et al., 2007, S. 35).
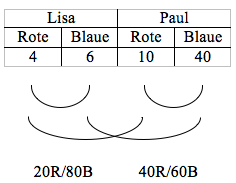
Wie oft ein Ereignis (z.B. die Ziehung der Farbe Rot) in einer Serie von Experimenten vorkommt, wird als „absolute Häufigkeit" bezeichnet (vgl. Panknin, 1972, S. 94). Beispielsweise zieht Lisa 4 rote Perlen, dann 6, dann 5 und schließlich nochmal 6.
Die absolute Häufigkeit ist jedoch nicht immer ausreichend, um Wahrscheinlichkeiten miteinander vergleichen zu können, da der Zufall dafür sorgt, dass die Ergebnisse in weiteren Wiederholungen streuen (vgl. Eichler & Vogel 2009, S. 168). Daher muss die absolute Häufigkeit im Verhältnis zur Anzahl der insgesamt durchgeführten Versuche betrachtet werden. Dieser Wert wird als relative Häufigkeit bezeichnet (vgl. Panknin 1972, S. 79):
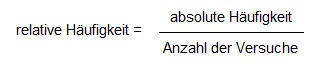
Bei der Durchführung von Zufallsexperimenten kommt man mit der gemessenen relativen Häufigkeit dem Wert für die Wahrscheinlichkeit des Auftretens eines Ereignisses umso näher, je größer der Umfang der durchgeführten Experimente gewählt ist (Gesetz der großen Zahlen) (vgl. ebd., S.84). So zeigt sich der Zufall in ausreichend Wiederholungen gar nicht mehr so „zufällig", sondern weist Muster auf (vgl. Eichler & Vogel 2009, S. 168).
"Argumentieren" in der Grundschule
Neben den inhaltsbezogenen Kompetenzen kann im Kontext des Wahrscheinlichkeitsbegriffs auch das Begründen im Kontext der prozessbezogenen Kompetenzen des Argumentierens geschult werden.
Das Argumentieren im Sinne von Beweisen ist in der Grundschule sicher nicht möglich (vgl. Krummheuer & Fetzer 2005, S. 29 ff.). In der Grundschule scheint sich eher ein Begriff des Argumentierens durchzusetzen, der in der Nähe des 'Begründens' angesiedelt ist (vgl. Fetzer 2011, S. 28). Diese Ebene des Argumentierens wird als substanzielles Argumentieren bezeichnet und geht in der Grundschule dem analytischen Argumentieren (Beweisen im deduktiven Sinne) voraus (vgl. ebd., S. 35).
Beim substanziellen Argumentieren bleibt auf argumentationstheoretischer Ebene eine gewisse Unsicherheit bestehen (vgl. Toulmin 2003, S. 116ff.). Diese Unsicherheit besteht aufgrund der Tatsache, dass die angeführte, allgemein hypothetische Aussage, nicht alle Informationen enthält, welche schließlich übermittelt werden. Im Bereich der Wahrscheinlichkeitsrechnung werden vielfältige Entdeckungen geboten, die eine Argumentationskompetenz herausfordern.
Im Kontext der Einstiegsaufgabe sollten die Kinder die Zuordnung von Wahrscheinlichkeiten begründen. Im Folgenden werden mögliche Lösungswege für die Bearbeitung der Aufgabe dargestellt.
Zuordnung von Wahrscheinlichkeiten begründen
In der dargestellten Einstiegsaufgabe werden zwei verschiedene Ziehungen aus unterschiedlichen Urneninhalten dargestellt.
Aufgabe der Kinder ist es, die Ziehungen den Inhalten zuzuordnen. Bei dieser Aufgabe handelt es sich um eine typische Aufgabe aus der Statistik. Gegeben sind zwei unbekannte Verteilungen von Perlen. Aus den Daten zweier Ziehungen soll auf die Verteilung geschlossen werden.
Es ist bemerkenswert, dass eine statistische Aussage nie mit 100%iger Sicherheit getroffen werden kann, da der Zufall immer Abweichungen zulässt (vgl. Wittmann & Müller 2009, S. 215). Es sind erst bei ausreichenden Wiederholungen Muster zu erkennen (vgl. Abschnitt ‚Wahrscheinlichkeiten bestimmen'). Jedoch kann angenommen werden, dass Lisa aus dem Säckchen mit 40 roten und 60 blauen Perlen zieht und Paul aus dem Säckchen mit 20 roten und 80 blauen Perlen.

Bei der Bearbeitung solcher Aufgabe erhält die Größe der Stichprobe eine besondere Bedeutung, da Lisa und Paul insgesamt unterschiedlich viele Perlen gezogen haben. Dies zeichnet auch den besonderen Schwierigkeitsgrad der Aufgabe aus. Denn aufgrund der verschiedenen Stichprobengröße lassen sich die einzelnen Perlenfarben nicht anhand der absoluten Häufigkeiten miteinander vergleichen. Sie müssen im Verhältnis zur Gesamtmenge betrachtet werden.
Schüler begründen Wahrscheinlichkeiten
Begründungstyp: Differenzvergleich zwischen den Ziehungen
Die Kinder vergleichen die beiden Differenzen der beiden Ziehungen.
Darstellung:
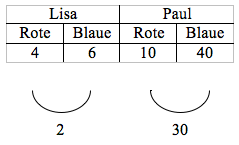
Beispiel:
Fabian: Paul hat aus dem Säckchen mit 20 roten und 80 blauen Perlen gezogen und Lisa aus dem Säckchen mit 40 roten und 60 blauen Perlen, denn Paul hat mehr von den blauen und nur ganz wenig von den roten Perlen. Lisa hat zwar auch mehr von den blauen und weniger von den roten Perlen, aber dafür nur zwei Unterschied und bei Pauls gezogenen Perlen sind es ja dreißig.
Begründungstyp: Absoluter Vergleich einer Perlenfarbe
Die Kinder vergleichen die absolute Anzahl einer Perlenfarbe miteinander.
Darstellung:
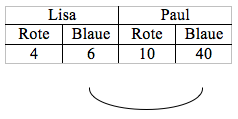
Beispiel:
Marvin: Lisa hat aus dem Säckchen mit 40 roten und 60 blauen Perlen gezogen, weil sie mehr blaue als rote Perlen hat. Bei Paul könnte das genau so sein, weil er auch mehr blaue Perlen hat.
Begründungstyp: Vergleich einer Farbe mit dem Inhalt des Säckchens
Die Kinder vergleichen eine Farbe der Ziehung mit dem Inhalt des Säckchens, indem sie die Anzahl der gezogenen Perlen einer Farbe von dem Inhalt des Säckchens einer Farbe abziehen.
Darstellung:
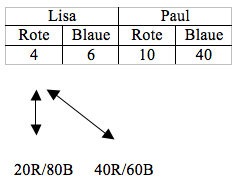
Beispiel:
Nina: Paul hat aus dem Säckchen mit 40 roten und 60 blauen Perlen gezogen, weil Lisa hat ja nur ganz wenige Rote gezogen und in dem Säckchen mit 20 roten und 80 blauen Perlen sind ja auch weniger rote Perlen drin.
Begründungstyp: Vergleich einer Farbe in Abhängigkeit von weiterer Farbe
Die Kinder betrachten beide gezogenen Perlenfarben in Beziehung zu beiden Säckchen.
Darstellung:
Beispiel:
Lena: Da Lisa im Verhältnis mehr rote Perlen hat, so muss sie aus dem Säckchen mit 40 roten und 60 blauen Perlen gezogen haben, auch wenn sie trotzdem mehr blaue Perlen hat. Paul hat aus dem anderen Säckchen gezogen, weil er mehr blaue (40) als rote (10) Perlen hat
Eigenaktivität
Vergleichen Sie die Begründungstypen miteinander und stellen Sie Unterschiede und Gemeinsamkeiten heraus.
Wo lassen sich Ihre Begründungen und die von Janosch einordnen (Anfangsbeispiel)?
Welche Probleme verbergen sich hinter diesen Begründungstypen? Warum sind die Begründungen der Kinder nicht ausreichend?
Verwenden die Kinder ihre Begriffserklärung aus Kapitel 2.1.2 zur Begründung der Zuordnung der Wahrscheinlichkeiten? Woran kann das liegen?
Probleme der einzelnen Begründungstypen finden Sie hier:
Wahrscheinlichkeiten: Probleme Begründungstypen
Insgesamt soll die vorliegende Seite deutlich machen, welche Rolle die prozessbezogene Kompetenz des Argumentierens im Kontext des Wahrscheinlichkeitsbegriffs spielen kann und dass man den Schülern genau zuhören muss, um zu verstehen, wie sie argumentieren.
Die größten Probleme zeigten sich im Zusammenhang mit den unterschiedlich großen Stichproben. Insbesondere die große Anzahl in der Stichprobe von Paul machte den Kindern das Problem bewusst. So gingen die Kinder sehr unterschiedlich dabei vor, ihre Entscheidungen, warum wer aus welchem Säckchen gezogen hat, zu begründen.
Festzuhalten ist jedoch, dass die meisten Versuche auf der Ebene der absoluten Häufigkeiten unternommen wurden und nur wenige Kinder den Vergleich zur Gesamtmenge heranzogen. Daher steht im Einstiegsbeispiel auch Janosch als Vertreter für viele Kinder, die ihre Entscheidung anhand des absoluten Vergleichs einer Perlenfarbe begründen. Weiterhin konnten die Beispiele in Abschnitt 2.1.2 zeigen, dass die Begründungen der Kinder meist alltagsbezogen waren und daher bei der Begründung zur Wahrscheinlichkeitszuordnung nicht zielführend sind.
Verwandte Themen
Kombinatorik
Kompetenzen im Mathematikunterricht
Zahlengitter
Reihenfolgezahlen
Schöne Päckchen
Weitere Anregungen zur Förderung prozessbezogener Kompetenzen im Kontext des Wahrscheinlichkeitsbegriffs finden Sie in den folgenden Texten:
Dehn, C., Mayer, S., Weisbach, D. & Neubert, B. (2007). Was ist wahrscheinlicher? Glücksrad- und Urnenaufgaben für die Grundschule. Grundschulunterricht, (2), 33-36.
Kurz, A. & Hoffart, E. (2008). „Da hat man einen Apfel mehr Glück." Schülerlösungen lösen Aufgaben zur Wahrscheinlichkeit. Grundschulunterricht Mathematik, (2), 29-32.
Pfeil, C. (2010). „Mit welchem WÜRFEL ist deine Gewinnchance größer?" Argumentieren und Verbalisieren zur Wahrscheinlichkeit. Grundschulunterricht, (2), 22-25.
Im PIKAS: Fortbildungsmodul: 'Entdecken, Beschreiben, Begründen' unseres Partnerprojekts PIK AS finden Sie Informations-, Unterrichts- und Fortbildungsmaterial zum Thema 'prozess- und inhaltsbezogene Kompetenzen'. Im PIKAS: Unterrichtsmodul: 'Daten, Häufigkeiten und Wahrscheinlichkeiten' unseres Partnerprojekts PIK AS finden Sie Unterrichtsmaterial und zahlreiche Anregungen.
Literatur
© Anne Tente für das KIRA-Team
