Auf den Seiten zu den Kapitänsaufgaben und zu „Kann das stimmen?" (Zeitungsmathematik) können Sie erfahren, dass Kinder häufig dazu neigen, schematisch mit Textaufgaben umzugehen. Sie schalten ihren gesunden Menschenverstand im schulischen Sachrechnen scheinbar aus.
Allerdings müssen wir Erwachsene bei der Interpretation der Kinderlösungen aufpassen, denn nicht selten steckt hinter den Lösungen der Schüler mehr, als es auf den ersten Blick erscheint. Im Folgenden können Sie interessante und auch verblüffende Schülerlösungen zu Textaufgaben zur Division mit Rest sehen und Sie werden erfahren, dass Kinder manchmal einfach anders denken.
Drei Eltern müssen stehen
Erstklässlern wurde folgende Aufgabe gestellt (vgl. Selter 2001):
Zu einem Elternabend kommen 81 Eltern. Es können immer 6 Eltern an einem Tisch sitzen. Wie viele Tische werden benötigt?
Der Erstklässler Max hat die Aufgabe wie folgt gelöst:

(Selter 2001, S. 167)
Eigenaktivität
- Wie würden Sie diese Aufgabe lösen?
- Betrachten Sie die Lösung von Max. Wie würden Sie im Unterricht mit Max Lösung umgehen?
Hintergrundwissen zur Division mit Rest
Im traditionellen Mathematikunterricht werden Textaufgaben dazu verwendet, erworbene Kenntnisse und Fertigkeiten anzuwenden, nachdem sie erklärt und an Aufgaben eingeübt wurden. Die Grundfertigkeiten werden auf diese Weise automatisiert (vgl. Rasch 2003, S. 4).
Hingegen sollen Textaufgaben im aktiv-entdeckenden Unterricht zu eigenständigem Überlegen und Lösen anregen. Dementsprechend sollten sie keine Routineaufgaben sein, vielmehr sollte das Lösen von Aufgaben des obigen Typs einen anspruchsvollen geistigen Vorgang darstellen, der eine gewisse Kompetenz an Problemlösevermögen erfordert.
Zahlreiche Studien (vgl. Silver et al. 1993; Verschaffel et al. 1994; Selter 2001) belegen, dass Kinder Schwierigkeiten mit problemorientierten Textaufgaben haben. Dabei äußern sich die Schwierigkeiten weniger in mangelnden rechnerischen Kompetenzen, sondern einerseits eher darin, die in der Aufgabe beschriebene Situation zu verstehen und sie in eine mathematische Gleichung umzusetzen (vgl. Stern 1992, S. 9).
Andererseits bereitet es den Kindern z.T. Probleme, die erzielten Ergebnisse zurück auf den Sachkontext zu beziehen (vgl. Selter 2001, S. 164). Als Gründe dafür werden die stereotype und einfache Natur der Mehrheit der schulischen Textaufgaben und die Art und Weise der Vermittlung genannt.
So wundert es nicht, dass Kinder dazu geneigt sind, Kapitänsaufgaben zu lösen, denn sie haben im Mathematikunterricht gelernt, dass jede Aufgabe eine Lösung haben muss. Befragt man aber die Kinder zu ihren Lösungen, erhält man erstaunliche Antworten (vgl. Selter & Spiegel 1997, S. 30 ff.).
Ähnlich verhält es sich bei Aufgaben zur Division mit Rest, denn hier wird aus den Kinderlösungen eine schematische Bearbeitung schnell offenbart (vgl. Selter 2001, S. 166).
„Im Gegensatz zu vielen anderen Textaufgaben ist hier nämlich mehr nötig als bloß die korrekte Ausführung der erforderlichen Rechnungen: Die eigentliche Schwierigkeit besteht häufig darin, den Rest situationsabhängig zu deuten bzw. überhaupt erstmal die Notwendigkeit zu erkennen, dieses zu tun" (Selter 2001, S. 166).
Trotz dieser Erkenntnisse muss beachtet werden, dass sich die Kinder gewiss Gedanken über die Aufgaben machen. Allerdings unterscheiden sich die Denkwege der Kinder oftmals und deutlich von denen der Erwachsenen, sodass die Erwachsenen Schwierigkeiten haben, diese zu verstehen (vgl. Selter & Spiegel 1997, S. 16 ff.).
Sie denken sprunghaft und unkonventionell, sie sind noch nicht durch Denkgewohnheiten und Denkschablonen gefesselt, „kurz: originell und kreativ" (Zehnpfennig 1995, S. 116 f.).
Das Aufgabenformat
Damit die Schüler zum Nachdenken über die Aufgaben angeregt werden, müssen die Aufgaben substanzhaltig und problemorientiert sein. Im Folgenden wird Ihnen ein mögliches Aufgabenformat vorgestellt.
Es handelt sich um Textaufgaben zur Division mit Rest, wobei für die Kinder die Schwierigkeit entsteht, den sich jeweils ergebenen Rest aufgabenangemessen zu interpretieren, d.h. den entstandenen Rest auf den Sachkontext der Aufgabe zurückzubeziehen und das Ergebnis aus dieser Perspektive zu deuten.
Der Einsatz solcher Aufgaben trägt zu einem Abbau der "Auto-Mathik" (Selter 2001, S. 165) während des Lösungsprozesses der Kinder bei und fördert die kritische Auseinandersetzung und die Aktivierung des Verstandes, wenn die Schüler die Chance erhalten, sich über ihre Vorgehensweisen auszutauschen und in einen produktiven Dialog zu treten.
Eigenaktivität
Hier sehen Sie eine kleine Auswahl solcher Textaufgaben (entnommen aus: Selter 2001) zur Division mit Rest. Überlegen Sie zunächst selbst, welche Lösungen Grundschulkinder nennen könnten.



Schülerdokumente zur Analyse
Im Folgenden sehen Sie nun verschiedene Schülerlösungen zu den oben vorgestellten Aufgaben.
Eigenaktivität
Überlegen Sie, wie die Kinder auf diese Lösungen gekommen sein könnten.
Bus-Aufgabe
Zu einem Auswärtsspiel wollen 820 Fußballfans mit dem Bus anreisen. In jedem Bus können 40 Fans mitfahren. Wie viele Busse müssen fahren?
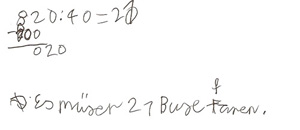
Maurice

Cedric
Feuerwehr-Aufgabe
Eine Firma stellt Feuerwehrschläuche her. Diese Firma produziert 820 Meter Schlauch pro Tag. Auf einer Rolle Feuerwehrschlauch sind 40 Meter. Wie viele Rollen stellt diese Firma pro Tag her?

Cedric

Maren
Elternabend-Aufgabe
Zu einem Elternabend kommen 81 Eltern. Sie sitzen an 13 Tischen. Wie viele Personen sitzen an einem Tisch?

Aryhan

Marie-Theres
Traktor-Aufgabe
Ein Traktor hat 294 Liter Benzin im Tank. Er verbraucht 12 Liter in einer Stunde. Wie viele Stunden kann der Traktor fahren, bis der Tank leer ist?
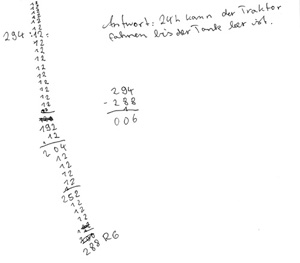
Alina
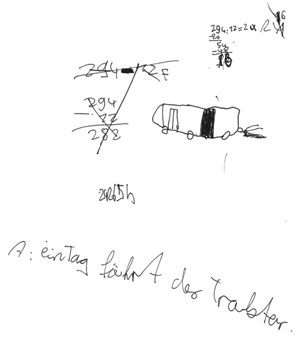
Cedric
Weiterführende Aufgabe
Eigenaktivität
Erfinden Sie selbst Aufgaben, bei denen die Kinder zu einem sinnvollen Umgang mit Textaufgaben im Mathematikunterricht angeregt werden können.
Verwandte Themen
- Kapitänsaufgaben
- Zeitungsmathematik
- Bauernhofaufgaben
Auf der Website unseres Partnerprojekts PIK AS finden Sie im PIKAS: Fortbildungsmodul: 'Gute Aufgaben' weitere Informationen sowie Fortbildungs- und Unterrichtsmaterialien zur Texterschließung und zur Bearbeitung komplexer Sachaufgaben.
Literatur
© Dena Ittmann für das KIRA-Team