Diese Seite soll Sie am Beispiel des Aufgabenformats Zahlenmauern (vgl. Wittmann & Müller 1990, S. 103 ff.) dazu anregen, sich mit der Frage auseinanderzusetzen, wie schriftliche Dokumente von Kindern zum „Entdecken, Beschreiben und Begründen" auch für die Leistungsfeststellung und -bewertung herangezogen werden können.
Prozessbezogene Kompetenzen feststellen und bewerten - eher etwas für „Einser-Kandidaten"?
Eigenaktivität: Betrachten Sie die Antworten zweier Lehrerinnen auf die Frage:
Inwiefern sollten Ihrer Meinung nach Aufgaben, die prozessbezogene Kompetenzen wie das Beschreiben und Begründen ansprechen, auch bei der Leistungsfeststellung und -bewertung eingesetzt werden?
Lehrerin 1: Ja (zögernd). Wobei es ist dann die Frage, wie stark gewichtet man die ganze Sache. Oder inwieweit sagt man so, naja das ist so was für ‚Einser-Kandidaten‘. Das man das also nicht so zum Standard für alle macht, sondern eher für denjenigen, der so eine richtig gute Zensur haben will ... So vielleicht.
Lehrerin 2: Ich weiß nicht, ob ich das konkret in einer Mathearbeit einbauen würde, weil ich glaube, dass das viele Kinder doch vom Schreiben her vom Zeitaufwand doch noch ganz schön in Beschlag nimmt, so dass dann nur wenig Zeit für die anderen Aufgaben ist.
Was würden Sie auf diese Frage antworten?
Auch prozessbezogene Kompetenzen zählen
Die Förderung von den prozessbezogenen Kompetenzen (in den Bildungsstandards wird auch von allgemeinen Kompetenzen gesprochen) hat in den letzten Jahren - nicht zuletzt durch die Inkraftsetzung der Bildungsstandards und des „neuen" Lehrplans für Mathematik in NRW - enorm an Bedeutung gewonnen.
Gemeinsam mit den inhaltsbezogenen Kompetenzen bilden sie die fachbezogenen Kompetenzen. Prozess- und inhaltsbezogene Kompetenzen stehen dabei nun gleichwertig nebeneinander und in einem wechselseitigen Zusammenhang - auch optisch verdeutlicht durch den Doppelpfeil in der folgenden Abbildung:
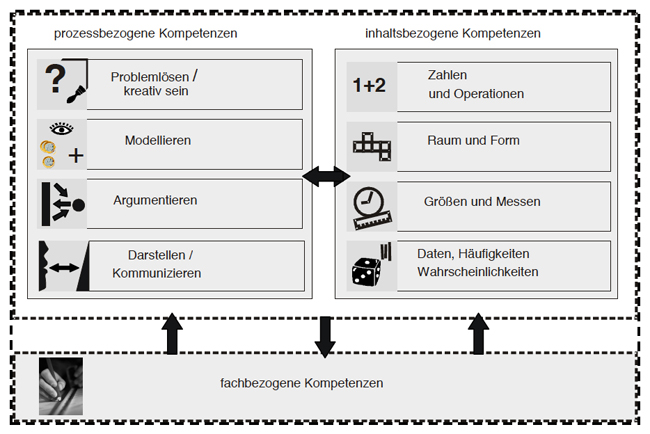
(MSW NRW 2008, S. 57)
Für die unterrichtliche Umsetzung bedeutet dies z.B.: Wenn inhaltlich zum Thema Addition gearbeitet wird, sollen auch prozessbezogene Kompetenzen, wie beispielsweise das Darstellen/Kommunizieren und Argumentieren berücksichtigt werden, denn „den allgemeinen mathematischen Kompetenzen ist eine herausragende Rolle bei der Entwicklung von auf Verständnis gegründeten inhaltlichen mathematischen Kompetenzen zugedacht." (Walther 2008, S. 20)
Auch in den bundesweiten Bildungsstandards wird die wichtige Rolle der prozessbezogenen Kompetenzen für die mathematische Bildung betont: „Das Mathematiklernen in der Grundschule darf nicht auf die Aneignung von Kenntnissen und Fertigkeiten reduziert werden. [...] Die allgemeinen mathematischen Kompetenzen verdeutlichen, dass die Art und Weise der Auseinandersetzung mit mathematischen Fragen ein wesentlicher Teil der Entwicklung mathematischer Grundbildung ist" (KMK 2005, S. 6).
Dabei sind die prozessbezogenen Kompetenzen eigentlich nichts Neues, denn auch im alten Lehrplan von 1985 waren sie - wenn auch mit anderen Begrifflichkeiten - bereits verankert, wie die folgende Abbildung zeigt:
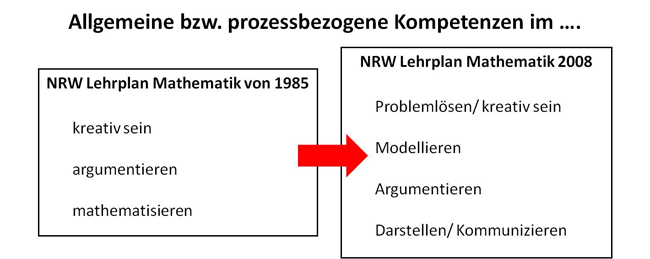
(vgl. Forthaus 2008)
Einen tatsächlichen „Durchbruch" der prozessbezogenen Kompetenzen, in dem Sinne, dass deren Bedeutung für das Mathematiklernen und eine entsprechende Förderung auch ernst genommen wird, lässt sich jedoch erst in den letzten Jahren beobachten. Mittlerweile finden sich vielfältige didaktische und methodische Vorschläge für einen zeitgemäßen Mathematikunterricht in Schulbüchern und der entsprechenden Fachliteratur.
Zu einem zeitgemäßen Mathematikunterricht gehört neben einer veränderten Aufgaben- und Lernkultur jedoch auch eine veränderte Leistungskultur (vgl. die Seite „Umgang mit den Leistungen der Kinder"), in der unter anderem auch prozessbezogene Kompetenzen genauso „zählen" wie inhaltsbezogene.
Dies scheint in der unterrichtlichen Umsetzung jedoch schwierig zu sein, wie es auch Walther et al. (2008) einräumen: „Ähnlich wie im Deutschunterricht das Beurteilen der Texte von Kindern in der Regel aufwändiger ist als die bloße Beurteilung der Fertigkeiten im Rechtschreiben, ist die Beurteilung von Aufgaben(teilen), die die allgemeinen Kompetenzen ansprechen, häufig nicht so unkompliziert wie die reine Bewertung des (End-)Resultats.
Aber Ersteres ist erforderlich und ausgehend von einem Kriterienkatalog auch leistbar, wobei man sich der unvermeidlichen Subjektivität der eigenen Wahrnehmungen durchaus bewusst, aber mit positiver Einstellung um individuelle Gerechtigkeit bemüht sein sollte" (Walther et al. 2008, S. 40).
Mit anderen Worten: Mit Kriterien wie „richtig" und „falsch" kommt man bei prozessbezogenen Kompetenzen nicht weiter. Denn was genau ist eine „richtige Lösung", wenn es bspw. um die Beschreibung und Begründung von Entdeckungen an Zahlenmauern (vgl. Wittmann & Müller 1990, S. 103 ff.) geht?
Des Weiteren ergeben sich natürlich in einem Mathematikunterricht, in dem z.B. entdeckt, beschrieben und begründet werden soll, auch andere Anforderungen an die Kinder. Insbesondere der hohe Anteil des produktiven Sprachgebrauchs in Mathematik wird hierbei deutlich. Die Bedenken der beiden Lehrerinnen aus dem Eingangsbeispiel sind daher sicherlich nachvollziehbar.
Diese Kompetenzen zu entwickeln ist ein langfristiger Prozess und nicht von heute auf morgen leistbar. Ebendarum müssen prozessbezogene Kompetenzen auch von Beginn an gefördert werden, denn „die Förderung der mündlichen und schriftlichen Ausdrucksfähigkeit (oder weiter gefasst: des „Darstellens") ist ein erklärtes, d.h. in den Lehrplänen festgeschriebenes Ziel des Mathematikunterrichts" (Krauthausen 2007, S. 1033).
Kinder müssen demnach immer wieder Gelegenheit haben, eigene Rechenwege zu erklären, entdeckte Muster und Strukturen zu beschreiben und Vermutungen für diese aufzustellen, sich in Mathekonferenzen darüber auszutauschen - und all das auch so darzustellen, dass andere sie verstehen. Dabei dürfen sie natürlich nicht allein gelassen werden. Ihnen müssen geeignete Werkzeuge angeboten werden, die ihnen dabei helfen.
Das Argument, dass diese Anforderungen insbesondere für Kinder mit Lernschwierigkeiten in Mathematik zu hoch seien und deshalb Aufgaben zum Beschreiben, Begründen und Darstellen eher als ‚nachgeordnetes Additum für leistungsstärkere Kinder' (vgl. ebd., S. 1029) zu sehen sei, hält sich dabei nach wie vor in vielen Köpfen - wie auch das Eingangsbeispiel zeigt.
Scherer (1997) gibt jedoch zu bedenken, dass „Schüler, die Schwierigkeiten beim Rechnen haben, [...] nicht unbedingt auch Schwierigkeiten beim Entdecken, Beschreiben und Erklären von Zusammenhängen haben [müssen]" (Scherer 1997, S. 47 f.) Auch diese Kinder gilt es also - ebenfalls mit entsprechender Hilfestellung - in diesem Bereich zu fördern und zu fordern.
Analyse von Schülerdokumenten
Prozessbezogene Kompetenzen feststellen und rückmelden
Wie bereits auf dieser Seite erwähnt und auf der Seite „Umgang mit den Leistungen der Kinder" auch weiter ausgeführt wurde, gibt es eine Vielzahl an unterschiedlichen Methoden, um die Leistungen der Kinder festzustellen. Insbesondere für die Leistungsfeststellung von prozessbezogenen Kompetenzen bieten sich selbstverständlich insbesondere solche Instrumente an, bei denen die Lernentwicklung der Kinder über einen längeren Zeitraum in den Blick genommen wird.
Lerntagebücher, Forscherhefte, Projekt- und Gruppenarbeiten mit Ergebnispräsentationen sind nur einige Beispiele. Dennoch können prozessbezogene Kompetenzen gelegentlich auch punktuell in den Blick genommen werden und beispielweise Bestandteil einer Klassenarbeit sein oder als eine Aufgabe für den Mathebriefkasten eingesetzt werden (vgl. „Umgang mit den Leistungen der Kinder").
Im Rahmen einer solchen schriftlichen Leistungsfeststellung wurde Drittklässlern (kurz vor den Osterferien) unter anderem die folgende Aufgabe gestellt, in der nicht das Rechnen im Mittelpunkt stand, sondern das Entdecken, Beschreiben und Begründen:
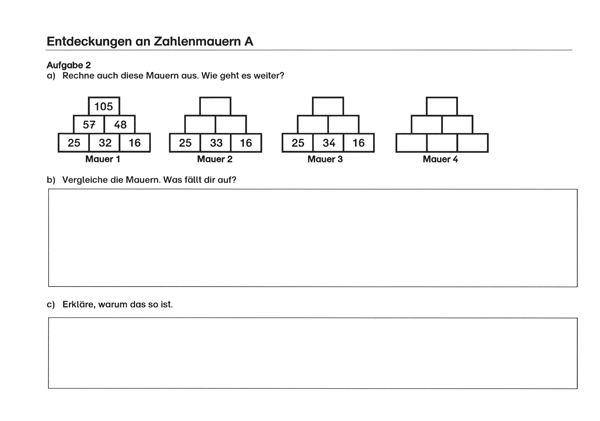
Eigenaktivität
- Lösen Sie die Aufgabe zunächst selbst.
- Wie sähe für Sie eine „optimale" Lösung eines Drittklässlers aus? Ziehen Sie hierbei auch die Kompetenzerwartungen des Mathematiklehrplans der Landes NRW für die Bereiche "Kommunizieren/Darstellen" und "Argumentieren" heran.
Auf der Seite „Umgang mit den Leistungen der Kinder" wurde bereits thematisiert, dass natürlich nur die im Unterricht behandelten Inhalte für die Leistungsfeststellung und -bewertung herangezogen werden können. Im Sinne einer „zieltransparenten Herausforderung" müssen dabei im Dialog mit den Kindern Zielsetzungen und Bewertungskriterien deutlich werden.
Eigenaktivität
Überlegen Sie deshalb:
- Was hätte vorher im Unterricht mit den Kindern thematisiert werden müssen, wenn diese Aufgabe (auch) für die Leistungsfeststellung und -bewertung dienen soll?
Dem pädagogischen Leistungsprinzip entsprechend, in dem die Leistungsfeststellung und -bewertung vorrangig dazu dient, Kinder in ihrer Lernentwicklung zu unterstützen und nicht zu überprüfen, ist auch eine angemessene und ermutigende Form der Rückmeldung notwendig. Diese dient dazu
- das Kind über den eigenen Lernstand zu informieren
- dem Kind Verbesserungsmöglichkeiten und Probleme aufzuzeigen
- gemeinsam mit dem Kind Absprachen zum Weiterlernen zu treffen
- das Kind zu motivieren.
Im Folgenden finden Sie die Bearbeitungen der Aufgabe von Lena, Carla und Benjamin.
Für eine größere Ansicht die Abbildungen anklicken.
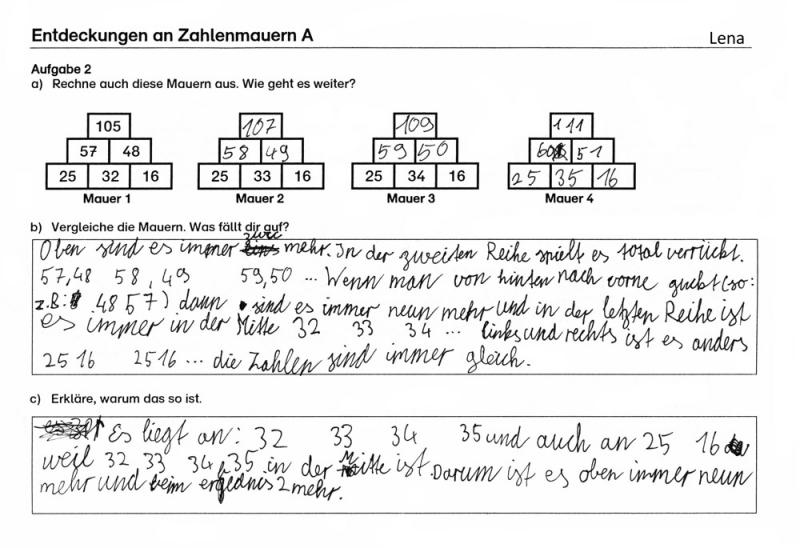
Lena
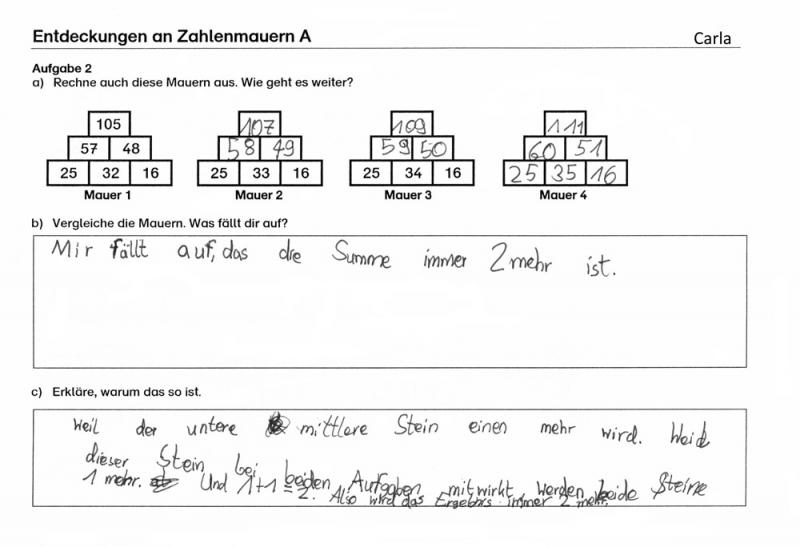
Carla
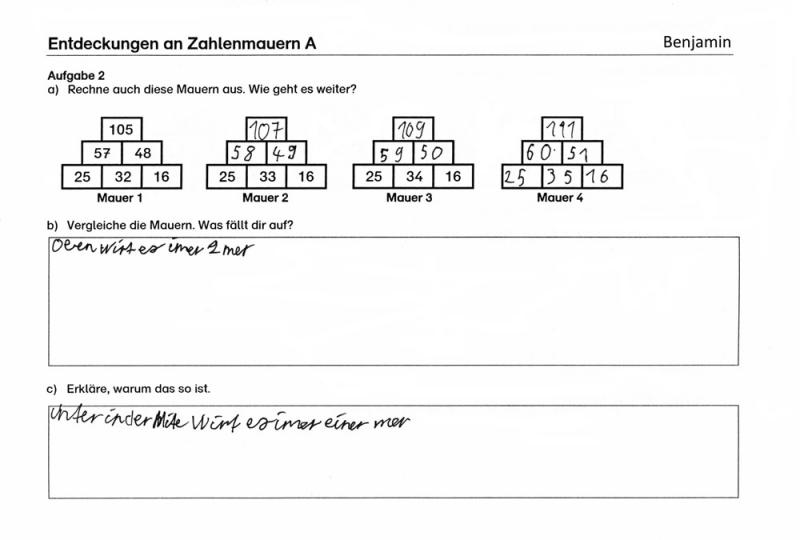
Benjamin
Eigenaktivität
Schreiben Sie an jedes der drei Kinder eine lernförderliche Rückmeldung.
Analysieren Sie dafür zunächst die Schülerdokumente hinsichtlich folgender Fragen:
- Was können die einzelnen Kinder schon?
- Was müssen sie noch lernen?
Hier finden Sie mögliche Analysen der drei Schülerdokumente, sowie eine mögliche Rückmeldung an das entsprechende Kind:
Prozessbezogene Kompetenzen bewerten
In der Schule müssen die Leistungen der Kinder nicht nur festgestellt, sondern auch bewertet werden. Dies haben Sie natürlich oben schon getan, indem Sie analysiert haben, was die drei Kinder bereits können und was noch nicht, d.h. die Leistungen der Kinder an Ihre Kriterien, eine zielbezogene Norm (Was sollte das Kind können?), angelehnt haben.
Bewerten heißt also nicht gleich benoten, aber auch letzteres ist in der Schule erforderlich. Umso wichtiger ist ein verantwortungsvoller Umgang mit den Leistungen der Kinder. Wie oben bereits betont wurde (vgl. auch „Umgang mit den Leistungen der Kinder"), sollten für eine umfassende Leistungsfeststellung und -bewertung im Mathematikunterricht ganz unterschiedliche Methoden zum Einsatz kommen - schriftliche Tests oder Klassenarbeiten sind dabei nur eine Möglichkeit von vielen.
Zudem können prozessbezogene Kompetenzen (wie es der Name schon sagt) natürlich auch nicht nur punktuell an einem einzelnen Produkt bewertet werden. Aber die obige Aufgabe kann durchaus auch - etwa nach einer Unterrichtsreihe zum Thema „Entdecken, Beschreiben und Begründen an Zahlenmauern" - Teil einer Klassenarbeit sein, die auch benotet wird.
Dafür ist es wichtig, sich über die eigenen Bewertungskriterien bewusst zu sein (vgl. Zitat von Walther et. al unter Punkt 2). Da diese Bewertungskriterien genauer als „gut", „mittel" oder „schlecht" sein sollten, machen wir an dieser Stelle einmal den Härtetest:
Eigenaktivität
Stellen Sie sich vor, die obige Aufgabe ist Teil einer Klassenarbeit und Sie haben genau 9 Punkte für diese Aufgabe zur Verfügung:
- Wie verteilen Sie diese 9 Punkte auf die Teilaufgaben a), b) und c)? Was sind Ihre Entscheidungskriterien, die Punkte so zu verteilen?
- Wie viele Punkte würden Sie Carla, Lena und Benjamin für ihre Bearbeitung der Aufgabe geben? Was sind Ihre Bewertungskriterien?
Selbstverständlich ist eine solche Bewertung abhängig von vielen Faktoren (hier z.B. die Behandlung von Zahlenmauern im Unterricht oder die individuellen Vorerfahrungen und Voraussetzungen der Kinder) und kann hier anhand dieser einzelnen Schülerdokumente sicherlich nicht umfassend erfolgen.
Insbesondere die individuelle Bezugsnorm kommt an diesen einzelnen Dokumenten demnach eindeutig zu kurz (vgl. „Die Bezugsnormen"). Auch gibt es bei der Bewertung (und Benotung) von prozessbezogenen Kompetenzen kein eindeutiges Rezept, bei dem die verwendeten Zutaten bloß abgehakt werden müssen.
Dennoch finden Sie hier - im Sinne der ebenfalls wichtigen anforderungsbezogenen oder kriterialen Bezugsnorm - mögliche aufgabenspezifische Kriterien, die bei einer Bewertung Orientierung geben können.
Weiterführende Aufgaben
Eigenaktivität
- Hier finden Sie die Punkteverteilung zur obigen Aufgabe von sechs Lehrerinnen. Inwiefern finden Sie Ihre eigenen Überlegungen darin wieder? Diskutieren Sie die unterschiedlichen Ergebnisse.
- Entwickeln Sie ein weiteres Beispiel für eine prozessbezogene Aufgabe, die im Rahmen von schriftlichen Leistungsfeststellungen zum Einsatz kommen kann. Formulieren Sie auch hier Ihre Bewertungskriterien.
Weitere Informationen zum Thema finden Sie auch auf unserer Partnerprojektseite primakom in den Modulen im Bereich "Leistungen"
Verwandte Themen
- Kompetenzen im Mathematikunterricht
- Die Bauernhofaufgabe
- Reihenfolgezahlen
- Schöne Päckchen
- Zahlengitter
- Tangram
- Kombinatorik
Selter, Ch. (2009). Der neue Lehrplan für die Grundschule. Eine Illustration durch zehn Unterrichtsbeispiele.
PIKAS: Entdecken, Beschreiben, Begründen (u. a. anhand von Entdeckerpäckchen)
PIKAS: Sprachförderung im Mathematikunterricht
PIKAS: Schriftliche Rückmeldungen bei Forscherheften zu Mal-Plus-Häusern
PIKAS: Beurteilen und Rückmelden
PIKAS: Kindersprechstunde
PIKAS: Lernstände wahrnehmen