Melanie

Im Gegensatz zu Jenny und Stefanie beherrscht Melanie den Umgang mit Überträgen schon. Ihr bereitet die Sutraktion zweier gleicher Zahlen noch Schwierigkeiten.
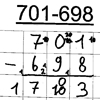
Sie berechnet die Aufgabe 701-698 mithilfe folgender Teilaufgaben:
- Einer: 11-8=3
- Zehner: 20- 0=10
- Hunderter: 17-9=7
- Tausender: 1=1
Insgesamt kommt sie auf das Ergebnis 1703.
Melanie führt die Subtraktion in der Einerspalte korrekt durch und führt auch den Übertrag richtig aus. Bei der Subtraktion in der Zehnerspalte ist sie sich jedoch unsicher, ob man innerhalb des Algorithmus 10-10=0 rechnen darf. Infolge ihrer Unsicherheit beschließt sie, dass man nicht 10-10 sondern 20-10 rechnen müsse. Da sie die 0 auf 20 erweitert, vermerkt sie einen Übertrag von 2 bei den Hundertern. Als Lösung der Teilaufgabe notiert sie den Einer der Lösung, also die 0. Den Zehner der Lösung notiert sie als Übertrag ebenfalls in der Hunderterspalte. Sie scheint an dieser Stelle auf die gewohnten Regeln der schriftlichen Addition zurückzugreifen.
Die Rechnung in der Hunderterspalte kommt durch die zahlreichen Überträge nicht ohne das Entbündeln eines Tausenders aus, sodass sich aus 7-(6+2+1) die Aufgabe 17-9 ergibt. Bei der Berechnung der Aufgabe unterläuft Melanie ein Einsminuseinsfehler, da sie 17-9=7 statt 17-9=8 rechnet. In Bezug auf die Teilaufgabe im Hunderterraum notiert sie angemessen im Bereich der Tausender eine kleine 1 als Übertrag. Unsicher, wie sie mit dieser schließlich umgehen soll, notiert sie die 1 auch als Ergebnis im Tausender.
Zusammenfassend lässt sich sagen, dass Melanie die wesentlichen Regeln der schriftlichen Subtraktion bereits verstanden hat, aber noch unsicher bei der Subtraktion zweier gleicher Zahlen ist. Deshalb entwickelt sie ihre ganz eigene Problemlösestrategie, bei der sie auf die ihr bekannten Regeln der schriftlichen Addition zurückgreift. Ihr Vorgehen ist also durchaus vernünftig, nur leider führt es nicht zum korrekten Ergebnis.

