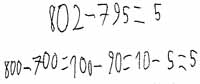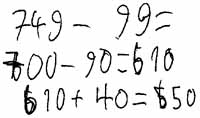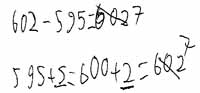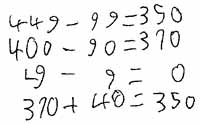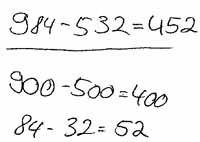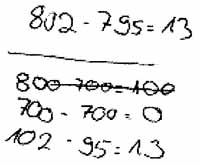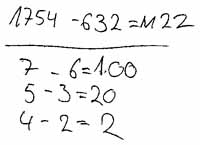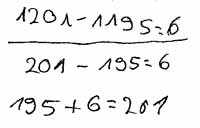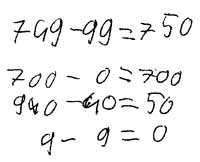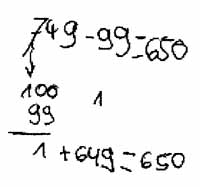Untersuchungen zur halbschriftlichen Subtraktion

Auf dieser Seite werden zentrale Untersuchungsergebnisse einer Bachelorarbeit zur halbschriftlichen Subtraktion von Tanja Wratschko vorgestellt. Sie hat sich im Rahmen ihrer Arbeit mit den halbschriftlichen Subtraktionsstrategien und den individuellen Problemen bei Aufgaben zur halbschriftlichen Subtraktion von zehn Drittklässlern auseinandergesetzt.

1. Kontextgebundene und kontextfreie Aufgaben
2. Zahlenraum unter und über 1000
3. Fehleranfälligkeit der Strategien
4. Verwandte Themen
5. Zitierte Literatur
6. Weiterführende Literatur

1. Kontextgebundene und kontextfreie Aufgaben

In der täglichen Arbeit mit Kindern kann man vielfach feststellen, dass kontextgebundene Aufgaben häufig anders gelöst werden als kontextfreie. Dies wurde im Rahmen der Bachelorarbeit von Tanja Wratschko genauer analysiert. Hierzu wurden den Kindern u.a. die folgenden vier Aufgaben vorgelegt:

a) 802 - 795
b) 749 - 99
c) Zu einer Schülerversammlung sollen 602 Kinder kommen. 595 Kinder sind schon da. Wie viele Kinder fehlen noch?
d) In einem Zoo gibt es 449 Tiere. Da der Zoo umgebaut wird, müssen 99 Tiere umziehen. Wie viele Tiere können im Zoo bleiben?

Die Aufgaben a) und b) sind kontextfreie Aufgaben, während c) und d) in einen Kontext eingebettet sind. In Aufgabe a) und c) ist bezogen auf die gewählten Zahlenwerte das Ergänzen eine günstige Strategie. In c) wird das Ergänzen durch den Kontext (595 Kinder von 602 Kindern sind schon da) zudem stark provoziert. Bei b) und d) bietet sich entweder eine Hilfsaufgabe oder das Vereinfachen an.

Timo rechnete die vier Aufgaben folgendermaßen: Aufgabe a) Aufgabe b) Aufgabe c) Aufgabe d) Versuchen Sie nachzuvollziehen, wie Timo gerechnet hat: Inwiefern wendet Timo die für diese Aufgaben günstig erscheinenden Strategien an? Was könnten mögliche Gründe sein, dass Timo so rechnet? Anmerkung: Wenngleich hierauf nicht der Fokus liegt, ist sicherlich auch Timos Notationsform seiner Rechenschritte in Aufgabe a) und c) interessant. Für ihn - wie für viele andere Kinder auch - stellt das Gleichheitszeichen keine Äquivalenzrelation (beide Seiten vom Gleichheitszeichen müssen gleichwertig sein) dar, sondern nur eine Aufforderung zum Rechnen. In Aufgabe a) unterläuft Timo außerdem ein kleiner Rechenfehler, denn er vergisst, die 2 von der 802 noch dazu zu addieren.

Hier finden Sie eine mögliche Interpretation zu Timos Rechnungen sowie weitere Befunde zu der Bedeutung des Kontextes hinsichtlich der Strategiewahl.

2. Zahlenraum unter und über 1000

Weiterhin stellt sich die Frage, ob ggf. auch der verwendete Zahlenraum einen Einfluss auf die Wahl der Strategie haben könne. Hierzu wurden den Kindern Aufgaben gestellt, die teilweise nicht mehr im aktuell behandelten Zahlenraum lagen. Folgende vier Aufgaben wurden den Kindern z.B. vorgelegt:

a) 984 - 532
b) 802 - 795
c) 1754 - 632
d) 1201 - 1195

Während Aufgabe a) und b) im Zahlenraum unter 1000 liegen, befinden sich die Aufgaben c) und d) im Zahlenraum über 1000. Dieser ist den Schülern bisher noch nicht bekannt. Aufgabe a) und c) legen keine besondere Rechenstrategie nahe, während in den Aufgaben b) und d) das Ergänzen günstig ist.

Michaela rechnete die vier Aufgaben folgendermaßen: Aufgabe a) Aufgabe b) Aufgabe c) Aufgabe d) Inwiefern scheint der unbekannte Zahlenraum die Wahl der Strategien von Michaela zu beeinflussen? Welche Gründe vermuten Sie hinter Michaelas Vorgehen? Anmerkung: In Aufgabe b) unterläuft Michaela in ihrer letzten Teilrechnung ein kleiner Rechenfehler.

Hier finden Sie eine mögliche Interpretation zu Michaelas Rechnungen sowie weitere Befunde zu der Bedeutung des Zahlenraums hinsichtlich der Strategiewahl.

3. Fehleranfälligkeit der Strategien

Bei der Analyse von typischen Fehlern stellt sich oftmals die Frage, ob es besonders fehleranfällige Strategien gibt. Bei den zehn befragten Drittklässlern traten beim Ergänzen und bei der Verwendung von Mischformen nur wenige Fehler auf. Der Grund für die geringe Fehleranfälligkeit beim Ergänzen ist sicherlich der, dass hier addiert wird, was vielen Schülern leichter fällt, als die Subtraktion. Die Ursache für die geringe Fehleranfälligkeit bei den Mischformen mag bei den zehn befragten Kindern daran liegen, dass sich die Schüler bei Anwendung ihrer eigenen Varianten vor allem in der Vorgehensweise sehr sicher zu fühlen scheinen. Studer und Hengartner (1999, S. 108) fügen noch hinzu, dass solche Vorgehensweisen vermutlich eher von Kindern verwendet werden, die bereits über ein differenziertes Zahlen- und Operationsverständnis verfügen, was sich auch in  Untersuchungsergebnissen von Wratschko größtenteils widergespiegelt hat. Es könnte hier also an der speziellen Schülerauswahl gelegen haben, dass diese Kinder wenige Fehler bei der Strategie "Mischformen" gemacht haben. In anderen wissenschaftlichen Untersuchungen konnte nämlich genau Gegenteiliges bzgl. der Strategie "Mischformen" festgestellt werden: Nach Benz (2005, S. 68f.) treten insbesondere bei der Strategie "Mischformen" die meisten Operationsfehler (= Benutzung falscher Rechenoperationen, Vergessen einer Teiloperation oder Verwendung einer falschen Teiloperation) auf.

Die meisten Fehler traten in Übereinstimmung mit einer Studie von Beishuizen (vgl. Beishuizen 1993 zitiert nach Padberg & Benz 2011, S. 202) beim stellenweisen Vorgehen auf. Die Dokumente von Pascal zeigen exemplarisch, welche Probleme die meisten Kinder bei der Durchführung dieser Strategie hatten.

Pascal hat Probleme beim stellenweisen Vorgehen, was daran gelegen haben könnte, dass diese Strategie für diese Aufgabe nicht besonders günstig und durchaus aufwendig ist. Thomas hingegen ist es mithilfe seiner Strategie gelungen, die Aufgabe richtig zu lösen. Pascal Thomas Beschreiben Sie, wie Pascal und Thomas vorgehen. An welchen Stellen unterlaufen Pascal Fehler?

Hier finden Sie eine mögliche Analyse von Pascals und Thomas Vorgehen.

4. Verwandte Themen

Halbschriftliche Subtraktion
Kira-Quiz

5. Zitierte Literatur

Beishuizen, M.  (1993).  Mental strategies and materials or models for addition and subtraction up to 100 in Dutch second grades. In: Journal for Research in Mathematics Education. H. 24 (4), S. 294-323.

Benz, C. (2005). Erfolgsquoten, Rechenmethoden, Lösungswege und Fehler von Schülerinnen und Schülern bei Aufgaben zur Addition und Subtraktion im Zahlenraum bis 100. Hildesheim, Berlin: Franzbecker.

Padberg, F. & Benz, Ch. (2011). Didaktik der Arithmetik. Für Lehrerausbildung und Lehrerfortbildung (4. erweiterte, stark überarbeitete Auflage). München: Spektrum akademischer Verlag.

Studer, Ch. & Hengartner, E. (1999). Strategien beim Subtrahieren dreistelliger Zahlen (3. Klasse). In: E. Hengartner (Hrsg.): Mit Kindern lernen. Standorte und Denkwege im Mathematikunterricht. Zug: Klett, S. 103 - 108.

6. Weiterführende Literatur

Selter, Ch. (2000). Vorgehensweisen von Grundschüler(inne)n bei Aufgaben zur Addition und Subtraktion im Zahlenraum bis 1000. In: Journal für Mathematikdidaktik. H. 2, S. 227 - 258.

Sundermann, B. & Selter, Ch. (1995). Halbschriftliches Rechnen auf eigenen Wegen. In: G. Müller & E. Ch. Wittmann (Hrsg): Mit Kindern rechnen. Frankfurt a.M.: Grundschulverband, S. 165 - 178.

Sundermann, B. & Selter, Ch. (1995). Halbschriftliche Addition und Subtraktion im Tausenderraum (I): Die Rechenmethoden der Schüler. In: Grundschulunterricht. H. 1, S. 22 - 25.

Sundermann, B. & Selter, Ch. (1995). Halbschriftliche Addition und Subtraktion im Tausenderraum (II): Die Rechenmethoden der Schüler. In: Grundschulunterricht. H. 2, S. 30 - 32.

© Tanja Wratschko für das KIRA-Team