Am Beispiel des Aufgabenformats "Wer trifft die 50?" (vgl. Steinbring 1995) wird auf dieser Seite aufgezeigt, welche Rolle das Prinzip der Fortschreitenden Mathematisierung bei den prozessbezogenen Kompetenzen spielt.
Dazu werden exemplarisch die Problemlösestrategien zweier Drittklässler analysiert und Entwicklungen dieser Strategien werden herausgestellt.
Fortschreitende Mathematisierung bei den prozessbezogenen Kompetenzen
Fortschreitende Mathematisierung wird in der Literatur bisweilen vor allem im Zusammenhang mit dem Einüben unterschiedlicher Algorithmen und Rechenverfahren, also den inhaltsbezogenen Kompetenzen, genannt (vgl. z.B. Treffers 1983).
Wie der Prozess der Fortschreitenden Mathematisierung beim Problemlösen oder den weiteren prozessbezogenen Kompetenzen aussieht, wurde bisher nicht untersucht.
Vor diesem Hintergrund hat Steinbach (2011) im Rahmen ihrer Masterarbeit erstmals eine entsprechende Untersuchung durchgeführt. Dabei wird die Fortschreitende Mathematisierung so verstanden, dass am Ende des Lösungs- bzw. Lernprozesses nicht wie bei den inhaltsbezogenen Kompetenzen die effizienteste Notationsform steht, sondern dass es um das Entwickeln eigener Strategien geht, die immer effizienter eingesetzt werden können.
Ob Kinder ausgehend von ihren selbst entwickelten Lösungsstrategien und denen ihrer Mitschülerinnen und -schüler im Austausch neue Wege kennenlernen, verstehen und diese dann auch flexibel nutzen, soll anhand des Aufgabenformats „Wer trifft die 50?" (vgl. Steinbring 1995) veranschaulicht werden.
Das Aufgabenformat "Wer trifft die 50?"
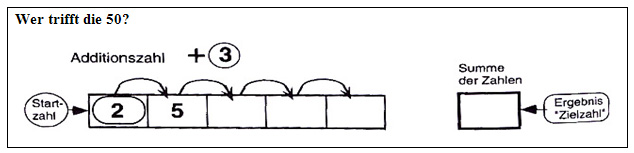
Abb. 1: Eine Zahlenreige mit 5 Feldern, Quelle: www.hermes.phl.univie.ac.at/schulmathematik/fileadmin/user_upload/Vortra...
Bei dem Aufgabenformat wird eine „Startzahl" im ersten Feld (z. B. 2) gewählt (siehe Abb.1). Anschließend bestimmt man eine „Additionszahl" und schreibt sie in den „Plus-Kreis" (z. B. 3). Die „Additionszahl" wird nun zur „Startzahl" addiert und das Ergebnis ins Feld rechts neben diese geschrieben. Dann wird die „Additionszahl" wiederum zu dem Ergebnis (hier 5) addiert und ins Feld daneben geschrieben. So wird auch in den weiteren Feldern vorgegangen.
Wenn alle fünf Felder der Zahlenreihe mit den jeweiligen Ergebnissen ausgefüllt sind, werden alle Zahlen addiert und die Summe der Zahlen, die „Zielzahl", im äußeren rechten Feld notiert (vgl. Steinbring 1995). Steinbring sieht dieses Aufgabenformat als Einstieg für die Berechnung von Zahlenreihen, bei denen die Glieder einen konstanten Abstand voneinander haben. Als Spezialfall gehört auch die so genannte „Gaußaufgabe" (1+2+3+4+...) dazu (vgl. Steinbring 1995, S. 224 ff.).
Untersuchung der Entwicklung von Problemlösestrategien
Im Rahmen ihrer Masterarbeit hat Steinbach (2011) eine Untersuchung zur Fortschreitenden Mathematisierung bei Problemlösestrategien durchgeführt. Dazu wurden einer dritten Klasse im Laufe einer von Steinbach entwickelten Lernumgebung folgende Aufgaben nacheinander gestellt:
1. Finde alle möglichen Zahlenreihen mit der Zielzahl 50.
2. Finde alle möglichen Zahlenreihen mit der Zielzahl 70.
Dabei wurde für das Aufgabenformat keine Strategie zum Lösen des Problems vorgegeben. Nach Aufgabe 1 und der damit verbundenen Entwicklung eigener Lösungsstrategien erhielten die Schülerinnen und Schüler durch einen gegenseitigen Austausch Einblicke in die Strategien und Entdeckungen ihrer Mitschüler. Somit bekamen sie die Chance, sich später in der zweiten Aufgabe an eventuell effizienteren Strategien oder bereits gemachten Entdeckungen zu orientieren.
Um Aussagen über die Problemlösekompetenzen der Schülerinnen und Schüler zu treffen und sie entsprechend fördern zu können, ist es wichtig, die Vorgehensweisen der Kinder durch verbale Äußerungen und schriftliche Dokumente zu verstehen und einzuordnen.
Anhand zwei ausgewählter Schülerbearbeitungen werden an dieser Stelle die einzelnen Schritte und die dabei gewählten Strategien verdeutlicht. Bei beiden Beispielen handelt es sich um Schüler, die in einem Interview ihre Strategien ausführlich erläutern. Daher können hier genauere Aussagen über die Vorgehensweisen getroffen werden.
Problemlösestrategien bei der Aufgabe "Wer trifft die 50?"
Der Vergleich wird zwischen einem mathematisch sehr leistungsstarken Kind und einem eher leistungsschwachen Kind gezogen. Die Informationen zur Einschätzung des Leistungstandes der Kinder wurden im Vorfeld in einem Gespräch mit der Lehrerin ermittelt.
An diesen Beispielen kann vor allem die Heterogenität der Schülerinnen und Schüler beim Bearbeiten der Aufgabe und beim Entwickeln der Strategien verdeutlicht werden.
Die Pfeile in der Tabelle (links) drücken die Beziehungen der einzelnen berechneten Zahlenreihen miteinander aus. Wird eine Strategie also über mehrere Zahlenreihen verwendet, sollen die Pfeile diesen Prozess verdeutlichen.
Analyse der Strategien von Tom beim Bearbeiten der Aufgabe „Wer trifft die 50?"

Tom ist ein sehr leistungsstarkes Kind und konnte im Interview schon nach der ersten Aufgabe die Beziehungen zwischen der Startzahl und Zielzahl nennen. Bei Aufgabe 1 bewegen sich seine Zielzahlen ausschließlich im Zahlenbereich von 40 bis 60 und er benutzt bei einigen Aufgaben sogar den negativen Zahlenbereich zur Lösung der Zielzahl 50 (vgl. obige Abbildung).
Er verwendet in seinen Bearbeitungen viele Strategien vom unsystematischen Probieren über das systematische Probieren hin zum Nutzen des vorausgegangenen Ergebnisses.
Analyse der Strategien von Jannis beim Bearbeiten der Aufgabe „Wer trifft die 50?"

Jannis wiederholt die dritte Klasse und weist laut Aussage der Lehrerin viele Schwierigkeiten in Mathematik auf. Sein Lösungsweg ist gekennzeichnet durch das Zusammenspiel von unsystematischem und systematischem Probieren, wie die oben stehende Übersicht verdeutlicht. Oft setzt Jannis Start-, Plus- und Zielzahl nicht in Beziehung zueinander.
In seinem zweiten Schritt ist beispielsweise zu sehen, dass er seine Startzahl trotz einer schon vorausgegangenen Ergebnisüberschreitung erhöht. Bei der Berechnung der Zielzahl, die in einem Zahlenbereich bis 150 liegt, unterlaufen ihm einige Rechenfehler. Doch auch Jannis kommt auf seinem Weg zu einer richtigen Lösung und zeigt gute Ideen und Gedankengänge eines Problemlösers.
Vergleich
Die Analysen der beiden Bearbeitungen zeigen, dass sowohl leistungsstarke als auch leistungsschwächere Kinder auf ihrem jeweiligen Niveau Strategien entwickeln und modifizieren, um mathematische Probleme zu lösen.
Die gewählten Strategien unterscheiden sich zwar hinsichtlich einiger Aspekte, wie zum Beispiel der Vielfalt, der (Dauer der) Anwendung und der Entwicklung im Laufe der Bearbeitung, doch es lassen sich auch Gemeinsamkeiten hinsichtlich einiger Strategietypen, wie z.B. bei dem systematischen Probieren erkennen.
Problemlösestrategien bei der Aufgabe "Wer trifft die 70?"
Um eine Veränderung der Vorgehensweisen beim Problemlösen im Sinne einer Fortschreitenden Mathematisierung feststellen zu können, werden die von den Schülerinnen und Schülern verwendeten Strategien des Forscherauftrags 1 „Wer trifft die 50?" mit denen des 2. Forscherauftrags „Wer trifft die 70?" verglichen.
Analyse der Strategien von Tom beim Bearbeiten der Aufgabe „Wer trifft die 70?"
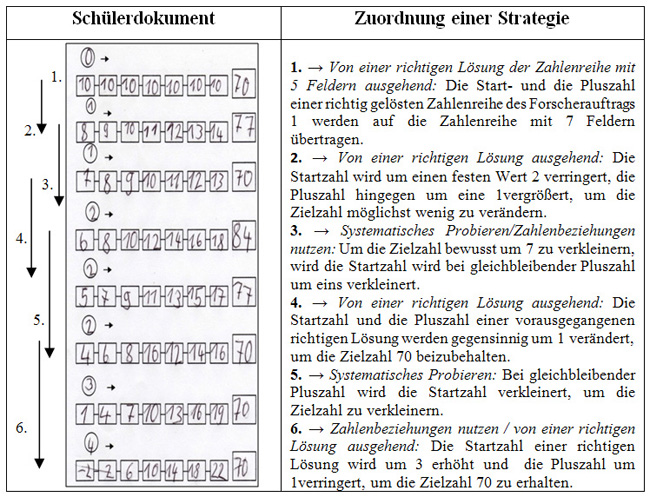
Tom findet bei seiner Bearbeitung sehr schnell alle möglichen Lösungen. Im Vergleich zu der Bearbeitung von Aufgabe 1 benutzt er häufiger die Zahlenbeziehungen zur Entwicklung seiner Lösungsstrategien. Er scheint sensibler für das Nutzen der Strukturen und Muster dieses Aufgabenformats, was man an seiner zuletzt gewählten Strategie erkennen kann (Startzahl minus 3, Pluszahl plus 1).
Er findet sogar eine weitere Lösung, als er seine Zahlenreihe in den negativen Zahlenraum ausbreitet. Er überträgt die gemachten Entdeckungen und entwickelten Strategien aus den vorherigen Forscheraufträgen mit fünf Feldern auf das Aufgabenformat mit sieben Feldern und kann sie problemlos anwenden, was schon die Wahl der ersten Zahlenreihe zeigt (10 + 10 + 10 + 10 + 10 + 10 + 10 = 70).
Er weiß auch ohne vorher zu berechnen, dass sich nun die Zielzahl um 7 verändert, wenn man die Startzahl um 1 verändert, was an seinem dritten Schritt erkennbar wird. Die Strategie des systematischen Probierens, die er bereits erfolgreich bei der Bearbeitung des ersten Forscherauftrags anwendete, kommt auch in dieser Bearbeitung vor. Auf das unsystematische Probieren verzichtet er jedoch komplett.
Analyse der Strategien von Jannis beim Bearbeiten der Aufgabe „Wer trifft die 70?"

Jannis' Bearbeitung ist - wie auch die Bearbeitung der Aufgabe 1 - durch ein Zusammenspiel des systematischen und unsystematischen Probierens gekennzeichnet. Auf den ersten Blick zeigt sich hier keine Veränderung seiner Vorgehensweise, doch bei genauerem Hinsehen entwickelt sich auch Jannis Bearbeitung weiter.
Seine bevorzugten Strategien sind hier das Verändern der Startzahl bei gleichbleibender Pluszahl und das Verändern der Pluszahl bei gleichbleibender Startzahl.
Beide Strategien haben ihn auch schon bei der vorherigen Bearbeitung zu einer richtigen Lösung geführt. Doch im Gegensatz zu seiner anfänglichen Aufgabenbearbeitung mit den Zahlenreihen aus fünf Feldern zeigt er eine größere Ausdauer hinsichtlich der Verwendung der Strategien. Schritt 7 und 8 beispielweise zeigen, dass Jannis konzentrierter und systematischer bei dem Einsetzen der Zahlen vorgeht, als zuvor.
Er berücksichtigt bei der Wahl der Strategien das Ergebnis der Zielzahl, was in der Bearbeitung des ersten Forscherauftrags an manchen Stellen fehlte.
Problemlösestrategien im Sinne einer Fortschreitenden Mathematisierung
Betrachtet man die Bearbeitungen der Kinder hinsichtlich der Entwicklung von Problemlösestrategien im Sinne einer Fortschreitenden Mathematisierung, so wird sowohl bei Tom als auch bei Jannis eine Weiterentwicklung der Problemlösestrategien sichtbar.
Diese Entwicklungen sind durch unterschiedliche Merkmale gekennzeichnet und haben auf einem individuellen Niveau stattgefunden. So entwickelt Tom neue Strategien, indem er die bekannten Strukturen und Muster nutzt, während Jannis sein Vorgehen modifiziert und verbessert ohne dabei neue Strategien zu entwickeln.
Die Untersuchung hat insgesamt gezeigt, dass sich der Beginn des Erkundungs- oder Problemlöseprozesses häufig durch die Strategie des unsystematischen oder unsystematisch erscheinenden Probierens, also des beliebigen Einsetzens von verschiedenen Zahlen auszeichnet. Im weiteren Verlauf des Prozesses wird hingegen immer häufiger auf die Strategie des systematischen Probierens zurückgegriffen.
Erst durch scheinbar wahlloses Einsetzen verschiedener Zahlen und den daraus gewonnenen Erkenntnissen können sich allmählich differenzierte und systematische Strategien ergeben. Dabei führt nicht jede der entwickelten Strategien zum richtigen Ergebnis, wie beispielsweise das Vertauschen der Startzahl und Pluszahl einer vorausgegangenen, richtig gelösten Zahlenreihe.
In den meisten Fällen wird die jeweilige Strategie dann allerdings schnell wieder verworfen oder aus ihr eine neue entwickelt. Doch auch hinter entwickelten Strategien, die nicht zum gewünschten Zielzustand führen, stecken häufig richtige Ansätze und kluge Ideen. Daher sind sie für den weiteren Verlauf des Problemlösens ein wichtiger und bereichernder Bestandteil, der zu jedem Entdeckungsprozess dazu gehört. Es gibt also keine „falschen" Strategien in einem Problemlöseprozess.
Wie die obigen Beispiele gezeigt haben, nutzen die Kinder in der Regel nicht nur genau eine Strategie, sondern wechseln zwischen verschiedenen Strategien im Verlauf des Lösungsprozesses. Eine Verwendung von Mischformen kann ebenfalls häufig beobachtet werden. Der Wechsel der Strategieform vollzieht sich in den meisten Bearbeitungen nach drei bis vier berechneten Zahlenreihen oder nach dem Erreichen der gesuchten Zielzahl 50.
Der Vergleich aller Bearbeitungen macht folgende zusammenfassende Aussage über die Entwicklung der Problemlösestrategien möglich. Die Kinder entwickeln im Sinne der Fortschreitenden Mathematisierung immer effizientere und elegantere Problemlösestrategien oder Wege dorthin.
Dabei nutzen sie immer häufiger die Zahlbeziehungen und Strukturen der Aufgabe, um eine Lösungsstrategie zu entwickeln. Natürlich werden auch die anfangs entwickelten Strategietypen genutzt, doch es lässt sich eine allgemeine Verschiebung - weg vom unsystematischen Probieren, hin zum Nutzen von Zahlbeziehungen - erkennen.
Die Entwicklung der Problemlösestrategien zeigt sich jedoch bei jeder Schülerin und jedem Schüler auf eine unterschiedlich ausgeprägte Art und Weise, wie die Beispiele von Jannis und Tom verdeutlichen.
Durch den sozialen Austausch und das Kommunizieren über die Aufgabe in einer Mathekonferenz entwickelten die Schülerinnen und Schüler immer weiterentwickelte Strategien. Es kann also festgehalten werden, dass eine Fortschreitende Mathematisierung beim Entdecken und Problemlösen zu erkennen ist.
Dadurch, dass in diesem Rahmen lediglich nur ein Vergleich in einer sehr kurzen Zeitspanne und anhand von zwei verschiedenen Aufgaben gezogen werden konnte, sind die Ergebnisse noch nicht aussagekräftig genug. An dieser Stelle könnte eine weitere Untersuchung ansetzen, um die Fortschreitende Mathematisierung des Problemlöseverhaltens der Schülerinnen und Schüler bei anderen, ähnlichen Aufgaben zu analysieren.
Verwandte Themen
Prozessbezogene Kompetenzen
Reihenfolgezahlen
Zahlengitter
Literatur
© Maren Steinbach für das KIRA-Team