Durch die Konfrontation mit vom Zufall abhängigen Ereignissen in den Medien und ihrer Alltagswelt (z.B. in Spielen wie „Mensch ärgere Dich nicht!") kommen Kinder schon frühzeitig mit Gewinnregeln und Gewinnchancen in Berührung. Im Mathematikunterricht der Grundschule soll daher die Aufmerksamkeit der Schülerinnen und Schüler vom zufälligen Einzelfall auf die Gesamtheit von möglichen Gewinnchancen gelenkt werden, damit sich keine Fehlvorstellungen festigen. Dafür ist die Fähigkeit der Bewertung von Gewinnregeln und der Abwägung von Gewinnchancen notwendig.
Im Rahmen ihrer Masterarbeit haben Mohr & Prigge (2012) mit Schülerinnen und Schülern der dritten Klasse zwei Lotteriespiele durchgeführt, bei denen unterschiedlich farbige Legosteine aus einem Säckchen gezogen wurden. Für die Beurteilung und Erstellung von Gewinnregeln bei diesen Spielen, müssen die Kinder alle möglichen Farbkombinationen von mehreren Legosteinen (Dreier- und Zweiertürme) finden und in Beziehung zur Durchführung des Lotteriespiels setzen (vgl. Abb. 1).
Auf der folgenden Seite werden die wesentlichen Ergebnisse vorgestellt und anhand vieler Schülerdokumente, die im Rahmen ihrer Arbeit entstanden sind, illustriert.
"Das wird ein Unentschieden...?"
In einem Lotteriespiel, bei dem zwei Spieler abwechselnd jeweils zweimal aus einem Säckchen, gefüllt mit einem roten, blauen und gelben Legostein, ziehen, diesen nach dem Zug wieder zurücklegen und die gezogene Farbe auf einem Spielplan festhalten, gelten folgende Gewinnregeln:
Spieler 1 gewinnt, wenn er als erstes einen blauen Legostein zieht. Spieler 2 gewinnt, wenn er zuerst einen roten Legostein zieht. Die Gewinnregeln sind somit für beide Spieler fair, d.h. jeder hat die gleiche Gewinnchance.
Bei der Durchführung des Spiels mit Sara und der Interviewerin zeigte sich folgender Spielausgang: Sara konnte neun Gewinne auf dem Spielplan notieren, die Interviewerin gewann fünfmal. Sechsmal hat keiner der Spieler gewonnen, weil die Ziehung nicht durch die Gewinnregeln abgedeckt war.
Eigenaktivität
Betrachten Sie den Spielplan und beantworten Sie die folgenden Fragen:
- Wie beurteilen Sie diesen Spielausgang, wenn Sie die Gewinnwahrscheinlichkeit bei Zufallsexperimenten beachten?
- Schätzt ein Kind der dritten Klasse den Spielausgang anders ein? Was vermuten Sie?
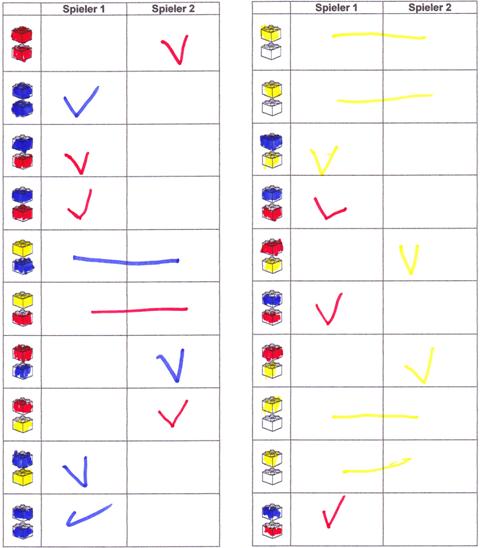
Wie Sara den Spielausgang beurteilt, können Sie im Kapitel 4 nachlesen.
Die Lotteriespiele
Im Folgenden werden die beiden Lotteriespiele, auf deren Grundlage die Schülerdokumente dieser KIRA-Seite entstanden sind, genauer erläutert. Dabei ist zu beachten, dass das Eingangsbeispiel beim Lotteriespiel B entstanden ist, während sich die Kinder zuerst mit dem Lotteriespiel A beschäftigten.
A:
Bei einem Lotteriespiel dürfen zwei Mitspieler abwechselnd jeweils dreimal aus einem Säckchen ziehen. In dem Säckchen befinden sich ein blauer und ein roter Legostein. Nach jedem Zug wird der Stein wieder in das Säckchen zurückgelegt, sodass er beim nächsten Zug erneut gezogen werden kann.
Es gibt zwei Gewinnregeln:
Spieler 1 gewinnt, wenn er nach dem dreimaligen Ziehen niemals die gleiche Farbe hintereinander gezogen hat.
Spieler 2 gewinnt, wenn er nach dem dreimaligen Ziehen mindestens einmal die gleiche Farbe hintereinander gezogen hat.
Suchen Sie sich die Gewinnregel aus, mit der Sie bei zwanzig Durchgängen wahrscheinlich am häufigsten gewinnen und begründen Sie Ihre Wahl!
B:
Bei einem anderen Lotteriespiel (siehe Beispiel „Das wird ein Unentschieden ..."?) dürfen zwei Mitspieler abwechselnd jeweils zweimal aus einem Säckchen ziehen. In dem Säckchen befinden sich nun ein blauer, ein roter und ein gelber Legostein. Wie beim ersten Spiel wird auch hier der Stein nach jedem Zug zurückgelegt.
Stellen Sie jeweils eine Gewinnregel für die beiden Mitspieler auf, sodass das Spiel fair ist.
Kombinatorischer Aspekt
Ohne längeres Überlegen würde fast jeder, der das oben beschriebene Lotteriespiel A mit einem Mitspieler durchführen will, sagen, dass es ihm gleichgültig ist, welchen Spieler er repräsentieren bzw. mit welcher Gewinnregel er gewinnen möchte.
Dass die Gewinnregeln relativ unfair formuliert sind, fällt erst bei einer intensiveren Auseinandersetzung mit allen möglichen Farbkombinationen, die bei der Ziehung entstehen können und schlussendlich über Gewinn oder Nicht-Gewinn entscheiden, auf.
Allgemein betrachtet ist das Lotteriespiel eine Abwandlung des mathematischen Urnenmodells. Basis des Urnenmodells ist ein Gefäß, in dem sich Gegenstände gleicher Form, z.B. Kugeln, befinden. Durch Ziehen dieser Gegenstände können eine Vielzahl von Zufallsexperimenten simuliert werden (vgl. Dehn, Mayer, Weisbach & Neubert 2007, S. 34).
Bei den hier vorgestellten Lotteriespielen sind diese Gegenstände gleicher Form Legosteine. Dabei befindet sich je ein roter und ein blauer Legostein bzw. im zweiten Lotteriespiel zusätzlich ein gelber Legostein in der Urne. Da der gezogene Legostein bei beiden Lotteriespielen zurück in die Urne gelegt wird, handelt es sich um ein Zufallsexperiment der Art Variation mit Wiederholung. Die Reihenfolge der gezogenen Legosteine ist dabei für das Gewinnen von entscheidender Bedeutung (vgl. Spiegel & Selter 2004, S. 294f.).
Die Anzahl aller möglichen Farbkombinationen bei Zufallsexperimenten dieses Typs lassen sich mit der Formel berechnen, wobei die Anzahl der Elemente die Anzahl der Ziehungen darstellt. Demzufolge gibt es im ersten Lotteriespiel acht verschiedene Farbkombinationen (23), die mit dem roten und blauen Legostein gezogen werden können und im zweiten Lotteriespiel neun verschiedene Farbkombinationen (32) der Farben Rot, Blau und Gelb.
Hoffmann (2003, vgl. S. 143ff.) kategorisiert in ihrer Dissertation die Strategien von Grund- und Sekundarschülerinnen und -schülern beim Lösen von Kombinatorikaufgaben in Mikro- und Makrostrategien. Mit Mikrostrategien bezeichnet sie dabei Strategien, die geeignet sind, lediglich aufeinanderfolgende oder Teile von Kombinationen zu finden. Mithilfe der Makrostrategien lassen sich hingegen alle Kombinationen generieren.


Im Folgenden wird eine Schülerlösung, welche eine typische Vorgehensweise erkennen lässt, exemplarisch vorgestellt:
Florians Lösung:


Florian baut zuerst die Türme auf und überträgt diese dann als Zeichnung auf ein weißes Blatt:
Er findet durch geschicktes Tauschen der Farben alle möglichen Kombinationsmöglichkeiten.
Zunächst baut er den Legoturm rot-blau-blau. Für seinen nächsten Turm bildet er das Gegenpaar. Alle Steine die blau waren, werden rot und umgekehrt. So erstellt der den Turm blau-rot-rot. Seine Lösungsmöglichkeit lässt sich der Makrostrategie der Gruppe 1 zuordnen, da er sämtliche Kombinationen durch Gegenpaarbildung findet.
Florians Lösungsmethode zeigt ein typisches Muster, welches in vielen Schülerlösungen in ähnlicher Form erkennbar ist: Er baut zuerst seine Gewinnmöglichkeiten auf und erst danach die des Mitspielers. Die einfarbigen Türme findet er zum Schluss.
Dass es darüber hinaus zusätzlich eine Vielzahl unterschiedlicher Lösungswege und -strategien gibt, zeigen die Schülerlösungen, die in Kapitel 3 zur Analyse vorgestellt werden.
Gewinnregeln und Spielausgänge beurteilen
Sowohl bei der Einschätzung bzw. Formulierung von Gewinnregeln als auch bei der Beurteilung von Spielausgängen benötigen die Kinder Argumentationsstrategien. Dabei sind das Erkennen von mathematischen Zusammenhängen einerseits und die Verbalisierung dieser Kontexte andererseits zwei verschiedene, sich bedingende Aspekte.
Das Erkennen vollzieht sich durch individuelle Gedankengänge, während eine Versprachlichung die Verwendung von Erklärungsmustern und entsprechenden Fachbegriffen erfordert. Demnach geht es in einer Argumentation darum, einen geschlossenen Gedankenzusammenhang zu verdeutlichen und eine getroffene Entscheidung verständlich zu machen, wohingegen ein Gespräch nicht zur Überzeugung des anderen dient (vgl. Ladenthin 2008, S. 9).
Der Mathematik-Lehrplan für Grundschulen in Nordrhein-Westfalen formuliert mit den prozessbezogenen Kompetenzen Argumentieren und Darstellen/Kommunizieren zwei Kategorien, die beschreiben, wie die Schülerinnen und Schüler lernen sollen, Beurteilungen von mathematischen Zusammenhängen vorzunehmen.
Somit umfasst das Argumentieren, Vermutungen über mathematische Zusammenhänge anzustellen und diese anhand von Beispielen zu prüfen. Durch das Vergleichen von Beispielen sollen allgemeine Betrachtungen angestrebt und schließlich Beziehungen und Regelhaftigkeiten mit Beispielen begründet werden.
Das Kommunizieren erfordert zum einen sich auf den Kommunikationspartner einstellen zu können und zum anderen die Verwendung von geeigneten Fachbegriffen (vgl. MSW NRW 2008, S. 60).
Die unter dem Begriff Argumentieren zusammengefassten Kompetenzen finden sich in der Aufgabenstellung des Lotteriespiels wieder. Zunächst sollen die Schülerinnen und Schüler Vermutungen über die Gewinnchancen bei bestimmten Gewinnregeln anstellen und anschließend bei der Durchführung des Spiels überprüfen.
Des Weiteren sollen Spielausgänge im Zusammenhang mit vorgegebenen und selbstaufgestellten Gewinnregeln beurteilt und Gewinnchancen eingeschätzt werden.
Die Einbeziehung all dieser Handlungen und Gedankengänge zum Lotteriespiel stellt für das Begründen hohe Anforderungen an die Schülerinnen und Schüler. Demnach sollte Kindern in Abhängigkeit ihres Leistungsvermögens mit Impulsen die Begründungsbedürftigkeit eines mathematischen Kontextes verdeutlicht werden.
Gleichzeitig ist die Anerkennung von Teilleistungen wichtig, denn das Erkennen von Mustern und Strukturen ist ein wichtiger Schritt auf dem Weg zur Formulierung von Begründungen, sodass die Entdeckungen entsprechend gewürdigt werden sollten (vgl. Bezold 2008, S. 37).
In diesem Kontext kann der Aufbau einer Argumentationskompetenz als Prozess verstanden werden, der sich aus folgenden Elementen zusammensetzt:

Abb. 2: Bausteine eines mathematischen Argumentationsprozesses
(Quelle: Bezold 2010, S. 3)
Die Heterogenität bei den mathematischen Tätigkeiten des Beschreibens, Schlussfolgerns und Begründens, welche mit dem Verständnis mathematischer Gegebenheiten einhergehen (vgl. Bezold 2010, S. 3), wird anhand der Schüleräußerungen im Kapitel 4 deutlich.
Um den Spielausgang beurteilen zu können, benötigen die Schülerinnen und Schüler die Gesamtanzahl möglicher Farbkombinationen als Argumentationsbasis. Daher müssen sie diese vor der Durchführung des Lotteriespiels bzw. vor der Formulierung eigener Gewinnregeln ermitteln. Verschiedene Vorgehensweisen, welche die Kinder beim Finden der Farbkombinationen gezeigt haben, werden im folgenden Kapitel dargestellt.
Vorgehensweisen beim Finden aller Farbkombinationen
Die nachfolgenden Schülerdokumente entstanden im Rahmen der Aufgabenstellung „Finde alle Möglichkeiten, die gezogen werden können!". Sie zeigen eine Auswahl der zahlreichen Strategien, welche die Schülerinnen und Schüler beim Lösen der kombinatorischen Aspekte des ersten und zweiten Lotteriespiels entwickelten.
Für die Lösung stehen den Kindern ausreichend Legosteine, Blanko-Papier und farbige Stifte zur Verfügung. Ihnen ist es frei überlassen, welche Hilfsmittel und welche Lösungsstrategien sie nutzen.
Eigenaktivität
- Welche Strategien erwarten Sie von den Kindern beim Finden aller Farbkombinationen am ehesten? Sie können sich dabei an den Kategorien von Hoffmann orientieren.
- Beschreiben Sie die Vorgehensweise der Kinder in den Beispielen. Welche Strategien wenden sie an? Ordnen Sie die Schülerdokumente den Gruppen nach Hoffmann zu!
Moritz:


Lukas:


Janina:


Sollten Sie Hilfe bei der Analyse benötigen, klicken Sie bitte hier.
Das Finden der acht bzw. neun möglichen Farbkombinationen der Lotteriespiele A und B dient als Grundlage für die Einschätzung von Gewinnregeln und die Beurteilung von Spielausgängen, weshalb im Folgenden Schüleräußerungen zu Spielverläufen und -ausgängen näher betrachtet werden sollen.
"Dann hat man Glück!" - wie Kinder die Spielausgänge begründen
Nach der Durchführung des Lotteriespiels ist die Reflexion des Spielausgangs von entscheidender Bedeutung, denn diese ermöglicht das vertiefende Verständnis von Zufallsexperimenten solcher Art.
Wie oben bereits beschrieben ist es wichtig, Argumentationsstrategien bereits in der Grundschule zu entwickeln. Die folgenden Merkmale bei Argumentationen von Grundschulkindern hat Fetzer (2007 & 2011) in einer empirischen Studie zu Schreibanlässen im Mathematikunterricht benannt:
- EINFACHE SCHLÜSSE: Aus einem Sachverhalt oder einer Tatsache wird unmittelbar etwas geschlossen, ohne dass dieses durch eine allgemeine Aussage legitimiert wird. Dazu zählen z.B. Einwort-Antworten (vgl. Fetzer 2011, S. 30 & S. 33).
- SUBSTANZIELLE ARGUMENTATIONEN: Die Begründung ist eher vage formuliert und es sind nicht alle Informationen enthalten, die einen eindeutigen Schluss ermöglichen (vgl. ebd., S. 35).
- GERINGE EXPLIZITÄT VON ARGUMENTEN: Die Begründung ist ungenau, weil z.B. eine Verdeutlichung, worauf sich bezogen bzw. wovon ausgegangen wird, fehlt (vgl. ebd., S. 37f.).
- VERBALES UND NON-VERBALES ARGUMENTIEREN: Die Argumentation vollzieht sich verbal und non-verbal. Wenn den Schülern eine sprachliche Argumentation schwer fällt, hilft ihnen das „Zeigen und Verweisen auf didaktische Materialien, die Tafel oder ihr Heft" (ebd., S. 42).
Vergleicht man diese Merkmale mit der im Lehrplan beschriebenen Argumentationskompetenz (vgl. 2.2 Gewinnregeln und Spielausgänge beurteilen), so werden Unterschiede bzgl. des Verständnisses vom Argumentieren deutlich. Es stellt sich die Frage, wann eine Argumentation als solche gilt bzw. wie umfassend die Begründung sein muss.
Wenn man bereits einfache Schlüsse als Argumentation ansieht, „so erscheinen manche Äußerungen der Schülerinnen und Schüler in einem anderen Licht" (ebd., S. 33). Das Potenzial vieler Aussagen von Kindern wird erst deutlich, wenn diese durch Impulse zu einer Begründung angeleitet werden (vgl. ebd., S. 47).
In diesem Sinne ist das Argumentieren im Mathematikunterricht der Grundschule sehr bedeutsam, wenngleich dieser Prozess kontinuierlich angeregt werden muss.
Durch die Analyse des Spielverlaufs, der Gewinnregeln und möglicher Farbkombinationen der Legosteine, können die Schülerinnen und Schüler zur Begründung des Spielergebnisses z.B. folgende Aspekte betrachten:
- Beurteilung der Farbkombinationen, bei denen ein Gewinn verbucht werden kann im Vergleich zur Gesamtanzahl aller Kombinationen (Bsp.: Beim Lotteriespiel B gibt es insgesamt neun Farbkombinationen. Lauten die Gewinnregeln z.B. so, dass ein Spieler bei rot-gelb und einer bei gelb-rot gewinnt, so können beide jeweils nur bei einer von neun Kombinationen gewinnen).
- Analyse der Chance, einen Gewinn zu erzielen, im Hinblick auf die Anzahl der zum Gewinn führenden Farbkombinationen (Bsp.: Wenn beide Spieler beim Lotteriespiel B nur eine Gewinn-Farbkombination haben, liegt ihre Gewinnchance jeweils bei 1/9).
- Vornahme eines Vergleichs der Gewinnchancen für die beiden Spieler nach den aufgestellten Gewinnregeln und dem tatsächlichen Spielergebnis (Bsp.: Bezüglich der Gewinnregeln haben beide Spieler die gleiche Gewinnchance, jedoch gewinnt Spieler 1 zufallsbedingt z.B. dreizehnmal und Spieler 2 nur siebenmal).
Der Ausgang des Spiels ist letztlich vom Zufall bestimmt, sodass die Schülerinnen und Schüler bestenfalls argumentieren, dass das tatsächliche Spielergebnis eines unter vielen möglichen ist. Das zuvor durchgeführte Gewinnspiel bietet den Kindern die Gelegenheit, eigene Erfahrungen mit dem Zufall zu machen und dieses als Experiment bewusst wahrzunehmen (vgl. Herget 1997, S. 4).
Das ist besonders wichtig, wenn man bedenkt, dass Kinder gewisse vorbestimmte Einstellungen zu den Themen Zufall und Wahrscheinlichkeit aus Alltagssituationen mitbringen. So vermuten Erwachsene und Kinder nicht selten, dass beim „Mensch ärgere Dich nicht!" die Sechs weniger häufig gewürfelt wird als die übrigen Zahlen (vgl. ebd.).
In diesem Kontext sollten die vorunterrichtlichen intuitiven Vorstellungen der Kinder, welche diese beim Spielen erworben und verinnerlicht haben, aufgegriffen und fachwissenschaftlichen Kenntnissen gegenübergestellt werden (vgl. Büchter et al. 2005, S. 2ff.).
Demnach sollte bei der Analyse von Schüleräußerungen stets beachtet werden, dass Lernende eher einzelne Ergebnisse betrachten, weil diese im Moment bedeutsam sind, wohingegen in der Stochastik Zufallsexperimente langfristig analysiert werden und dabei z.B. auf das empirische Gesetz der großen Zahlen verwiesen wird (vgl. ebd., S. 6).
Das empirische Gesetz der großen Zahlen besagt, dass „die relative Häufigkeit mit zunehmender Zahl an Wiederholungen eines Zufallsexperiments sich stabilisiert und scheinbar einem bestimmten Wert zustrebt" (Schnell 2011, S. 9).
Nach der Darlegung von Argumentationsansätzen im Bereich von Zufallsexperimenten, sollte demzufolge bei der Analyse von Kinderäußerungen sowohl die Perspektive der Kinder als auch die fachliche Perspektive der Stochastik einbezogen werden.
Die nachfolgenden Kinderdokumente und Transkripte beziehen sich auf die Beurteilung des Lotteriespiels B, bei dem rote, blaue und gelbe Legosteine gezogen werden konnten.
Eigenaktivität
- Analysieren Sie die Beurteilungen der Kinder zum Spielausgang im Hinblick auf die drei oben aufgelisteten Aspekte sowie das Verständnis der Kinder in Bezug auf die Zufälligkeit des Ergebnisses.
- Betrachten Sie außerdem, inwieweit sich die von Hoffmann beschriebenen Merkmale bei Argumentationen von Grundschulkindern in den Transkripten wiederfinden lassen.
- Schauen Sie sich noch einmal das Einführungsbeispiel „Das wird ein Unentschieden...?" an und vergleichen sie Ihre eigene Beurteilung des Spielausgangs mit der nachfolgenden Erklärung von Sara.
Sara:

(I = Interviewerin)
I: Warum ist denn das Lotteriespielergebnis von uns beiden so unterschiedlich, obwohl wir doch beide die gleiche Gewinnchance hatten?
S: Ähm, das ist so ... dann hat man Glück, weil man dann meistens einfach so die Farben zieht ... wenn man hingucken würde, dann würde es vielleicht das gleiche Ergebnis sein, aber man guckt ja dabei nicht hin und zieht einfach die Farben und dann kann das auch so passieren.
Janina:

I: Wie kommt es, dass du häufiger gewonnen hast als ich, obwohl wir nach den Gewinnregeln die gleiche Gewinnchance hatten?
J: Ich hab fast immer Rot gezogen!
I: Aber du hättest ja auch Gelb oder Blau ziehen können, oder?
J: Ja, aber (sagt lange nichts) ich kann das nicht erklären.
I: Versuch es mal. Du hast ja schon richtig gesagt, dass du oft Rot gezogen hast, aber du hättest auch Gelb oder Blau ziehen können. Meinst du denn, das Spielergebnis hätte auch anders aussehen können? Guck dir die Farbkombinationen der Legosteine, die du eben aufgezeichnet hast, noch einmal an!
J: (sagt lange nichts) Ich weiß es nicht.
Ahmet:

I: Wie bewertest du die Gewinnregeln? Waren die für uns beide wirklich gleich gut?
A: Ja, die sind fast gleich gut, weil du hast dreimal gewonnen und ich viermal!
I: Und wie erklärst du dir, dass so oft gar keiner gewonnen hat? Woran kann das liegen?
A: Weil wir immer sonst Blau gezogen haben, da konnten wir gar nicht gewinnen (zeigt auf die Farbkombinationen, die einen blauen Legostein enthalten). Wenn wir aber zuerst Gelb oder Rot gezogen haben, dann gab es noch die Möglichkeit, dass wir nochmal die gleiche Farbe ziehen und gewinnen.
Moritz:

I: Du hast ja zwei faire Gewinnregeln aufgestellt. Wie kommt es dann, dass wir nicht gleich häufig gewonnen haben?
M: Manchmal haben wir auch andere hier gezogen ... andere Farben. Wenn man Gelb als erstes gezogen hat, hat man so oder so verloren, aber da oder hier (zeigt auf den Spielplan), da konnte man das noch nicht genau wissen ... da musste man noch einmal ziehen.
I: Genau! Und wenn du dir alle Möglichkeiten, die man ziehen kann, anguckst, bei wie vielen konnten wir gewinnen und bei wie vielen nicht?
M: Bei zwei konnten wir gewinnen und bei eins, zwei ... (zählt) bei sieben konnten wir nicht gewinnen. Aha ... deswegen gab es öfter keinen Gewinner!
Verwandte Themen
Kompetenzen im Mathematikunterricht
Kombinatorik
Wahrscheinlichkeiten einschätzen
Gewinnwahrscheinlichkeiten
Ausführlichere Erläuterungen zu den Mikro- und Makrostrategien sowie den einzelnen Unterstrategien finden
Sie im folgenden Text:
Hoffmann, A. (2003). Elementare Bausteine der kombinatorischen Problemlösefähigkeit.
Weitere Informationen zu den genannten Merkmalen von Argumentationen sowie entsprechende Folgerungen für die Unterrichtspraxis finden Sie in:
Fetzer (2011). Wie argumentieren Grundschulkinder im Mathemathematikunterricht? Eine argumentationstheoretische Perspektive.
Auf der Website des Partnerprojekts PIK AS finden Sie im PIKAS: Fortbildungsmodul: 'Entdecken, Beschreiben, Begründen' Fortbildungs-, Unterrichts- und Informationsmaterial. Außerdem wird im PIKAS: Unterrichtsmodul: Daten, Häufigkeiten und Wahrscheinlichkeiten Unterrichtsmaterial zum Thema Zufallsexperimente präsentiert.
Material
Interviewleitfaden
Literatur
© Lisa Mohr & Daniela Prigge für das KIRA-Team