Um Kinder in ihrem Lernen zu unterstützen und weiterzubringen, ist es nötig, sich in ihre individuellen Denkwege hineinzuversetzen. Dies gilt besonders, wenn die Kinder ganz andere Vorstellungen von bestimmten mathematischen Sachverhalten haben als Erwachsene und diese Vorstellungen zu Fehlern führen.
Wie solche Fehlvorstellungen aussehen können und dass diese häufig trotzdem logisch nachvollziehbar sind, zeigen wir auf dieser Seite am Beispiel der schriftlichen Subtraktion. Hier können Sie Ihr Wissen über typische Fehler bei der schriftlichen Subtraktion vertiefen und an ausgewählten Schülerdokumenten Ihre Diagnosefähigkeiten unter Beweis stellen.
Bea rechnet 713-281 schriftlich
Eigenaktivität
Schauen Sie sich die Rechnung von Bea an. Dort hat sich ein Fehler eingeschlichen. Verstehen Sie, wie Bea zu ihrer Lösung kommt?
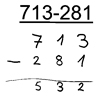
Mithilfe des Videos können Sie Ihre Vermutung überprüfen:
Hintergrundwissen zur schriftlichen Subtraktion
Bei der schriftlichen Subtraktion gibt es verschiedene Verfahren, die sich im Wesentlichen in der Art des Übertrags unterscheiden, aber auch dadurch, dass bei einigen spaltenweise ergänzt, bei anderen spaltenweise subtrahiert wird.
Noch bis vor ein paar Jahren (und teilweise auch noch heute) haben die Lehrpläne der einzelnen Bundesländer genau vorgeschrieben, welche(s) Verfahren gelehrt werden durfte (darf). Das hat sich teilweise geändert. So ist es in NRW beispielsweise mittlerweile der Lehrperson freigestellt, welche(s) Verfahren sie im Unterricht thematisiert (vgl. MSW NRW 2008).
Typische Fehler und Schwierigkeiten bei der schriftlichen Subtraktion
Hinter der schriftlichen Subtraktion steckt ein nicht unkomplizierter Algorithmus. Und auch wenn die Durchführung der schriftlichen Subtraktion geübten Erwachsenen trivial erscheinen mag, so sind die verschiedenen Verfahren für die Kinder nicht immer von vornherein einsichtig.
Mitunter abhängig vom gewählten Verfahren, aber auch abhängig von der Bauart der Aufgabe, gibt es bei der schriftlichen Subtraktion viele Hürden, die es für die Kinder zu überwinden gilt. Dabei bedarf es der individuellen Unterstützung durch die Lehrperson.
Um diese Unterstützung leisten zu können, ist es wichtig, die Schwierigkeiten und Fehlvorstellungen der Kinder im Zusammenhang mit der schriftlichen Subtraktion nachvollziehen zu können. Deshalb wollen wir Ihnen im Folgenden einen Überblick über die Stolpersteine und typischen Fehlern bei der schriftlichen Subtraktion geben. Einige Fehler werden anhand von Schülerdokumenten und/oder Videos veranschaulicht.
Häufig auftretende Schwierigkeiten (in Anlehnung an Padberg & Benz 2011, S. 256 ff.) sind z.B.:
1. Schwierigkeiten mit dem Übertrag
Fehlertyp: Generell keine Übertrage
Beispiel:
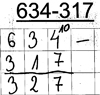
Stefanie erweitert die Einerziffer des Minuenden korrekt, macht aber nicht den nötigen Übertrag zur Zehnerziffer des Subtrahenden.
Fehlertyp: Kein Übertrag in die leere(n) Stelle(n)
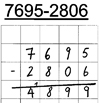
Beispiel:
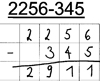
Simon vergisst, den nötigen Übertrag in die Tausenderspalte zu notieren.
Fehlertyp: Übertrag bei der Subtraktion zweier gleicher Ziffern
Beispiel:
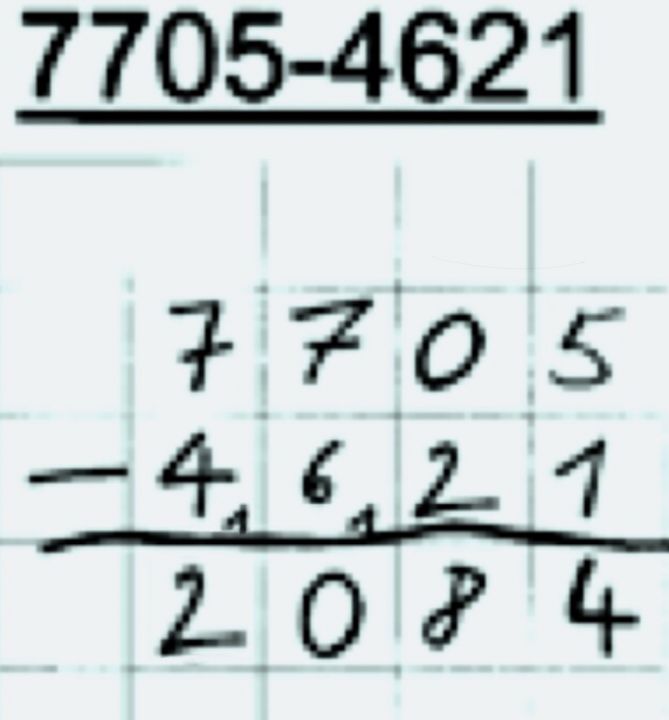
Fehlertyp: Ein Übertrag zu viel
Beispiel:
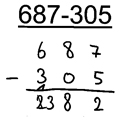
Öznur macht einen Übertrag in die Hunderterspalte, obwohl die Zehnerziffer im Minuend größer ist als die Zehnerziffer im Subtrahenden.
2. Fehler mit der Null
Fehlertyp: 0 - x = 0
Beispiel:
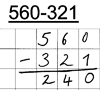
Sven rechnet 0 - 1 = 0 und notiert somit auch nicht den Übertrag in die Zehnerspalte.
Fehlertyp: x - 0 = 0
Beispiel:
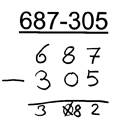
Bea ist sich unsicher, wie sie mit der Null im Subtrahenden umgehen soll und rechnet zunächst 8 - 0 = 0.
Fehlertyp: Kein Übertrag zur Null
Beispiel:
Michael notiert keinen Übertrag in der Zehnerspalte zur Null des Subtrahenden.
Fehlertyp: Kein Übertrag nach der Null
Beispiel:
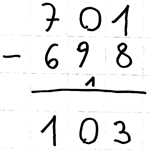
Benjamin macht die Überträge bei anderen Aufgaben richtig. Doch als eine 0 im Zehner des Minuenden auftritt, erweitert er diese korrekterweise auf 10, macht dann aber keinen Übertrag zum Subtrahenden der Hunderterspalte.
3. weitere Fehler
Fehlertyp: Rechenrichtungsfehler (von links nach rechts statt andersherum)
Beispiel:

Wenn die Kinder eine schriftliche Subtraktion von links nach rechts (also in ihrer gewohnten Schreibrichtung) durchführen, kann es zu Fehlern bei den Überträgen kommen, die sich so nicht ohne weiteres durchführen lassen, wie das Beispiel von Bea verdeutlicht.
Fehlertyp: Addition statt Subtraktion
Beispiel:
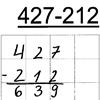
Maja addiert die Ziffern des Minuenden und Subtrahenden stellenweise.
Fehlertyp: Spaltenweise Unterschiedsbildung
Beispiel:

Metin zieht permanent die größere von der kleineren Ziffer ab.
Fehlertyp: Falsches Stellenwertverständnis (die Aufgabe wird nicht stellengerecht untereinander geschrieben)
Beispiel:

Farina notiert Minuend und Subtrahend nicht stellengerecht untereinander und subtrahiert somit auch nicht stellenweise.
Fehlertyp: Schwierigkeit durch unterschiedliche Stellenanzahl
Beispiel:
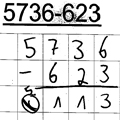
Jessica ist sich unsicher, wie sie mit der unterschiedlichen Stellenzahl von Minuend und Subtrahend umgehen soll.
Fehlertyp: Vermischen mehrerer Verfahren
Beispiel:
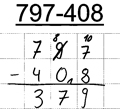
Tom erweitert die Einerziffer des Minuenden korrekt und macht auch den nötigen Übertrag zur Zehnerziffer des Subtrahenden. Allerdings mischt er sein Vorgehen mit der Entbündelungs-Technik an der Zehnerziffer des Minuenden.
Fehlertyp: Einsundeinsfehler
Beispiel:
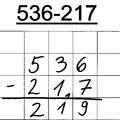
Frederieke rechnet 5H - 2H = 2H.
Nun haben Sie schon einiges über Fehlertypen und Schwierigkeiten bei der schriftlichen Subtraktion erfahren.
Eigenaktivität
Erfinden Sie selbst Aufgaben zur schriftlichen Subtraktion, die möglichst schwer sind.
Begründen Sie Ihre Auswahl.
Überträge
Wie sich bei genauerer Betrachtung der typischen Fehler zeigt, hängen diese häufig mit den Überträgen zusammen. Deshalb haben wir Kinder darum gebeten, zu erklären, was der Übertrag bedeutet und wann dieser nötig ist. Die Erklärungen der Kinder sind in den folgenden Videos ersichtlich.
Abdul
Indira
Melanie
Ein Fehler allein ist noch keine Fehlvorstellung
Die obige Auflistung zeigt Einzelbeispiele zu den verschiedenen Fehlertypen. Wenn es jedoch darum geht, eine allgemein gültige Aussage über mögliche Fehlvorstellungen und Schwierigkeitsbereiche des Kindes zu machen oder einen Fehler bei einer bestimmten Aufgabe überhaupt zu verstehen, hilft einem nur die Analyse mehrerer Aufgaben.
Auf der Seite Informative Aufgaben wird am Beispiel des Viertklässlers Thomas verdeutlicht, wie wichtig es ist, sich mehrere, vergleichbare Aufgaben eines Kindes anzuschauen.
Analyse von individuellen Fehlern
Auch wenn es viele typische Fehler bei der schriftlichen Subtraktion gibt, so ist nicht jedes fehlerhafte Vorgehen der Kinder einer dieser Kategorien zuzuschreiben. Häufig ist das Vorgehen der Kinder sehr individuell und manchmal treten auch mehrere Fehler gleichzeitig auf.
Eigenaktivität
- Betrachten Sie die folgenden Schülerlösungen und versuchen Sie, diese zu beschreiben und zu begründen.
- Schauen Sie sich erst dann die Videos an (auch mehrfach!) und vergleichen Sie das Vorgehen der Kinder mit Ihren Vermutungen.
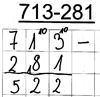
Stefanie
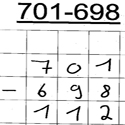
Jenny
Hier finden Sie eine mögliche Interpretationzu Stefanie.
Hier finden Sie eine mögliche Interpretation zu Jenny.
Weiterführende Aufgabe
Die (Fehl-)Lösung von Melanie ist besonders individuell und sehr schwer zu durchschauen.
Auch für den/die Fortgeschrittene/n wird die Analyse nicht ganz einfach sein.
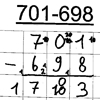
Eigenaktivität
Analysieren Sie die (Fehl-)Lösung von Melanie.
Hier finden Sie eine mögliche Interpretation.
Testen Sie Ihr Wissen zu dem Thema in unserem Kira-Check.
Verwandte Themen
Informative Aufgaben
Halbschriftliche Addition
Halbschriftliche Subtraktion
Schriftliche Addition
Schriftliche Multiplikation
Schriftliche Division
Um Fehler besser zu verstehen ist es wichtig, die verschiedenen Verfahren der schriftlichen Subtraktion zu kennen.
Klicken Sie hier um einen Überblick über die Verfahren zu bekommen.
Materialien zum Thema 'Rechnen auf eigenen Wegen' sowie 'Vom halbschriftlichen zum schriftlichen Rechnen' finden Sie auf der Website des Projekts PIK AS im PIKAS: Fortbildungsmodul: 'Lernen auf eigenen Wegen'.
Auf der Homepage des Projekts PriMaKom („Primarstufe Mathematik kompakt“) erfahren Sie, wie Sie das sogenannte Dienesmaterial (primakom: Übergreifendes: Prinzipien: Materialeinsatz: Unterricht) (oder auch Mehrsystemblöcke) zur Veranschaulichung der schriftlichen Rechenverfahren einsetzen können. Darüber hinaus finden Sie auf dieser Selbstlernplattform, die in erster Linie für fachfremd unterrichtende Lehrerinnen und Lehrer eingerichtet wurde, weitere kompakt dargestellte Informationen zum Material.
Material
zur Fehleranalyse (701 - 698) Interviewleitfade
Literatur