"Kinder rechnen anders als andere Kinder" (Spiegel & Selter 2003, S. 22). Dieser Satz bringt zum Ausdruck, was wahrscheinlich jede Lehrperson täglich herausfordert und fasziniert: die heterogenen Rechenwege und -kompetenzen der Kinder.
Wie kann es aber gelingen, dass Kinder ausgehend von eigenen Rechenwegen neue kennenlernen, verstehen und diese dann auch flexibel nutzen, ohne dass man sie ihnen vordiktiert?
Die im folgenden Verlauf vorgestellte Lernumgebung zur Entwicklung flexibler Rechenstrategien (vgl. Lüling 2010; Götze & Lüling 2010) gibt Anregungen, wie dies gelingen kann.
Sophies "Rechentrick"
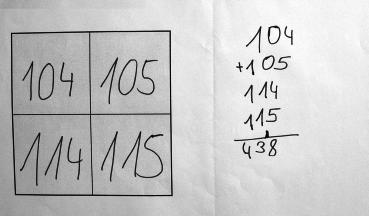
Drittklässler wurden aufgefordert, die Summe aller vier Zahlen eines 2x2 Ausschnitts aus dem Tausenderbuch (Wittmann & Müller 2002) möglichst geschickt zu bestimmen (vgl. Lüling 2010; Götze & Lüling 2010). Die Drittklässlerin Sophie hat sich den unten abgebildeten Ausschnitt ausgesucht und zur Berechnung der Summe benutzt sie einen für sie geschickten "Rechentrick".
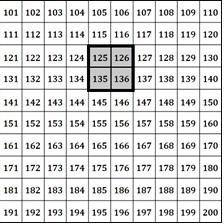
Eigenaktivität

- Wie würden Sie die Summe der vier ausgewählten Zahlen im 2x2 Feld möglichst geschickt bestimmen?
- Verstehen Sie, wie Sophie gedacht hat? Man erkennt, dass Sophie viele kluge Überlegungen anstellt, allerdings auch Fehler begeht. Welche klugen Überlegungen stellt sie an? Welche Fehler begeht sie? Wie können Sie diese erklären?
- Welche anderen Möglichkeiten zur Bestimmung der Summe sehen Sie? Wie könnten andere Kinder die Summe bestimmen?
Hintergrundwissen zum flexiblen Rechnen
Wie würden Sie die Summe des im Eingangsbeispiel dargestellten 2x2-Ausschnittes des Tausenderbuches bestimmen? Denkbar wären vielfältige Vorgehensweisen, z.B.
- könnte jeder Summand in seine Stellenwerte zerlegt und einzeln addiert werden (100+100+100+100=400; 20+20+30+30=100; 5+6+5+6=22; 400+100+22=522),
- könnten die Summanden einer Zeile geschickt addiert werden, da es sich um eine "fast Verdopplung" handelt (125+126=251; 135+136=271; 251+271=522), hier könnte zudem die erste Summe (251) geschickt genutzt werden, um die zweite schnell zu bestimmen (pro Summand 10 mehr, also insgesamt wird die Summe um 20 größer, also 271),
- werden die Summanden einer Spalte addiert (125+135=260; 126+136=262; 260+262=522). Auch hier könnte man die erste Summe (260) nutzen, um die zweite schnell zu bestimmen (pro Summand 2 mehr, also insgesamt wird die Summe um 2 größer, also 262),
- wird der kleinste Summand vervierfacht. Dann fehlen noch 22, da 126 um ein, 135 um zehn und 136 um elf größer ist als 125 (1+10+11=22). Dies muss noch hinzuaddiert werden (analog könnte man auch den größten Summanden vervierfachen und 22 abziehen),
- könnte man ausnutzen, dass die Diagonalensummen gleich groß sind: 125+136=261 und 126+135=261; 261+261=522,
- kann das Ergebnis mit Hilfe des schriftlichen Normalverfahrens ermittelt werden,
- (...)
Jeder dieser Lösungswege führt zum richtigen Ergebnis, doch: Welche Vorgehensweise erweist sich bei diesem speziellen Ausschnitt aus dem Tausenderbuch als besonders effizient und geschickt?
Die Kompetenz, vor dem Lösen einer Aufgabe einen geeigneten Rechenweg aus einem vorhandenen Repertoire an halbschriftlichen Strategien auszuwählen, bezeichnet Selter (1999, S. 8) als "flexibles Rechnen".
Eine Untersuchung von Rathgeb-Schnierer (2006) verdeutlicht, dass Rechenwege durch vielfältige Faktoren beeinflusst werden: Zahlwahrnehmung, Wissen über Zahlen und Rechenoperationen, Verfügen über strategische Werkzeuge, etc.
Der Weg zum flexiblen Rechnen kann nur ein individueller, vom Kind gesteuerter Weg sein (vgl. untenstehende Abbildung aus Rathgeb-Schnierer 2006, S. 277. Klicken Sie für eine Vergrößerung auf das Bild).
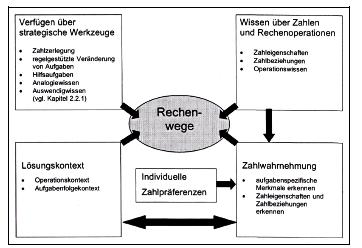
Der Mathematikunterricht sollte die Kinder daher immer wieder zur Reflexion und Kommunikation über Denkprozesse, Lösungswege und Rechenideen anregen. "Durch Kooperation und Kommunikation wird den Lernenden die Gelegenheit geboten, ihre verschiedenen individuellen Perspektiven darzustellen und zu diskutieren" (Rathgeb-Schnierer 2006, S. 44).
Die Kinder erhalten somit Einblicke in die unterschiedlichen Lösungswege ihrer Mitschüler und können sich an eleganteren und effizienteren Vorgehensweisen orientieren (vgl. Selter 1995, S. 11). Dadurch werden sie angeregt, Rechenwege der Mitschüler auszuprobieren und die eigenen Vorgehensweisen zunehmend zu vereinfachen und zu optimieren.
In ihrem individuellen Tempo gelangen die Kinder somit "von umständlichen, informellen Versuchen zu gezielten, aufgabenadäquaten und begründeten Vorgehensweisen" (Rathgeb-Schnierer 2006, S. 46).
Treffers (1983) spricht in diesem Zusammenhang von "fortschreitender Schematisierung". Aufgabe der Lehrperson ist es, Raum für Reflexionen im sozialen Kontext zu schaffen, wodurch die Kinder angeregt werden über die Grenzen ihrer aktuellen Fähigkeiten hinauszugehen und die "Zone der nächsten Entwicklung" (vgl. Wygotski 1987, S. 83 ff.) zu erreichen. Hierzu bedarf es manchmal einer gezielten Anregung durch die Lehrperson.
Gleichzeitig wird man durch dieses Vorgehen jedem Kind individuell gerecht, denn es kann - im Sinne einer natürlichen Differenzierung - stets selbst bestimmen, welche Rechnungen, Rechenwege und Notationsweisen es wählt.
Analyse der "Rechentricks" verschiedener Kinder
Im Folgenden sehen Sie einige Kinderdokumente aus einer dritten Klasse (entnommen aus Lüling 2010)
Eigenaktivität
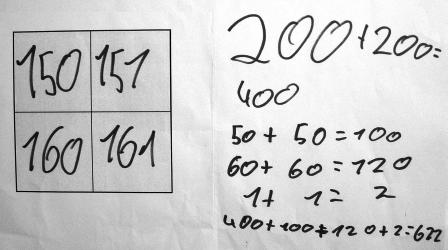
- Wie berechnen die Kinder die Summen der jeweiligen 2x2-Ausschnitte des Tausenderbuches? Welche Zahlbeziehungen nutzen die Kinder?
- Inwiefern würden Sie die Vorgehensweisen der Kinder als "geschickt" einstufen? Begründen Sie!
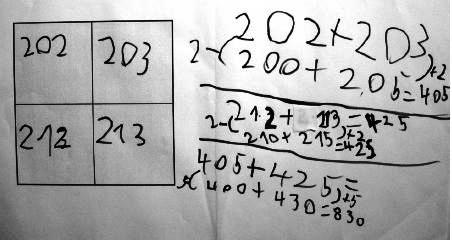


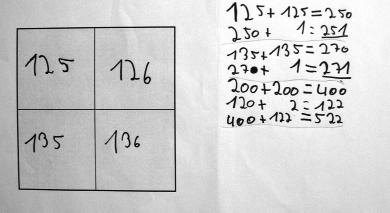

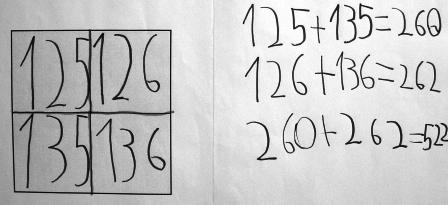
Entwicklung der Rechentricks von Anna
Wie im Hintergrundwissen bereits angedeutet, wurden die Kinder durch die Lernumgebung "Wir entdecken Rechentricks im Tausenderbuch" gezielt angeregt, über die Geschicktheit der eigenen Rechentricks nachzudenken und zunehmend für sie neue Rechentricks auszuprobieren (vgl. Lüling 2010; Götze & Lüling 2010).
Hierzu wurden ausgewählte Kinderrechentricks gemeinsam im Sitzkreis besprochen und für alle sichtbar an der Tafel aufgehängt. Wichtig ist in diesem Zusammenhang zu erwähnen, dass die Kinder dieses Vorgehen bereits aus dem zweiten Schuljahr kannten, d.h. bereits im zweiten Schuljahr wurde über verschiedene Rechentricks bei zwei Summanden diskutiert und die Kinder hatten dort bereits viel Zeit, sich mit verschiedenen halbschriftlichen Additionsstrategien zu beschäftigen.
Sie sehen im Folgenden die Entwicklung eines eher leistungsschwächeren Kindes namens Anna.
Eigenaktivität
- Analysieren Sie in den ersten drei Rechnungen, welche (verschiedenen) individuellen Rechenwege/Rechentricks Anna zur Bestimmung der Summe einschlägt. Inwiefern nutzt sie flexibel andere Strategien oder bleibt sie konsequent bei einer?
- Achten Sie auch darauf, wie Anna die Geschicktheit ihrer eigenen Rechnungen begründet. Was würden Sie Anna z.B. im Rahmen eines persönlichen Gespräches oder einer Kindersprechstunde rückmelden?
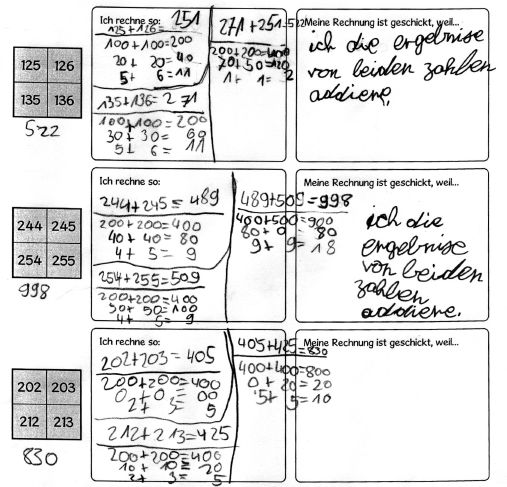
Nach der Phase, in der jedes Kind zunächst mit eigenen Rechentricks gerechnet und Anna für sich die obigen Rechentricks notiert hat, kam eine Reflexionsphase im Sitzhalbkreis vor der Tafel. Dort bekamen die Kinder die Gelegenheit eigene Rechentricks vorzustellen und neue von ihren Mitschülern kennen zu lernen. Unter anderem wurde hierbei der Rechentrick von Alex thematisiert, der - wie er selbst sagte - "über Kreuz" gerechnet hat:
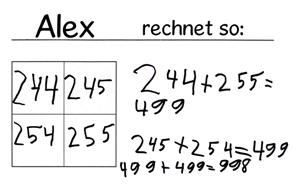
Selbstverständlich wurde auch besprochen, warum Alex so rechnen darf und warum dieser Rechentrick besonders geschickt ist: 244+255 zu rechnen ist sehr einfach, und die Summe 499 muss dann nur verdoppelt werden, was in diesem Fall auch leicht ist.
In der darauf folgenden Stunde fand der Rechentrick von Alex in Annas Forscherheft erstmalig Anwendung:
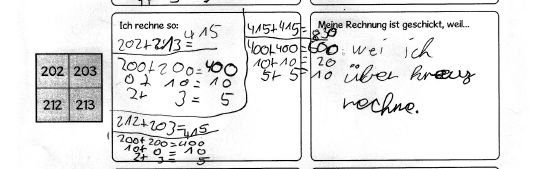
Es ist natürlich zu erkennen, dass Anna die Summen der über Kreuz gewählten Summanden dennoch mit der Strategie "Stellenwerte extra" bestimmt. Auch nutzt sie noch nicht die Erkenntnis, dass sie die Summe von 202 und 213 einfach nur zu verdoppeln braucht. Sie rechnet beide Summen "über Kreuz" komplett aus.
Letztlich mischt sich also ihre alte Strategie mit der neuen von Alex, so dass man hier bestätigt sieht, was Selter (2003, S. 40) betont: "Jede nicht selbst entwickelte Rechenstrategie ist für die Kinder immer auch Lernstoff und bedarf der wiederholten Übung. Und das auch über die Schuljahre hinweg".
Für den weiteren Unterricht gilt es, Anna darin zu bestärken, den Rechentrick von Alex komplett zu durchdringen und in ihr Repertoire an Rechentricks aufzunehmen.
Verwandte Themen
Halbschriftliche Addition
Auf der Website unseres Partnerprojekts PIK AS finden Sie im PIKAS: Selbststudiumsmodul: 'Lernen auf eigenen Wegen' weitere Informationen und Texte zum Thema 'flexibles Rechnen' und 'Umgang mit Eigenproduktionen'.
Weitere Anregungen, wie unterschiedliche Rechentricks im Rahmen von Mathekonferenzen unter den Kindern vorgestellt und besprochen werden können, bietet das PIKAS: Unterrichtsmodul: 'Sprachbildung- Mathekonferenzen'.
Im PIKAS: Selbststudiumsmodul: Beurteilen und Rückmelden: Informationsmaterial: Videos können Sie erfahren, wie Sie im Rahmen einer Kindersprechstunde den Kindern eine individuelle Rückmeldung zur Entwicklung ihrer Rechentricks geben können. Solche Gespräche können auch genutzt werden, um Probleme bei einzelnen Rechentricks mit dem Kind zu besprechen.
Material
Forscherheft inklusive einem "Trickheft" zur Notation aller neuen Rechentricks.
Das Forscherheft stammt aus Lüling 2010. Teile des Forscherheftes sind erschienen in: Götze & Lüling 2010
Literatur