In den vergangenen Jahren wurde immer wieder eine stärkere Betonung des Überschlagsrechnens gefordert. Dies geht einher mit der Kritik, dass die Bedeutung dieses zentralen Themas der Grundschulmathematik nicht selten auf die reine Anwendung der Rundungsregeln beschränkt wird. Auf dieser Seite werden wesentliche Aspekte des Überschlagsrechnens dargestellt und der Eigenwert dieses Themas aufgezeigt.
Am Beispiel der Aufgabenformate „Wie viel ungefähr?" und „Reicht das Geld?" werden verschiedene Überschlagsstrategien, die auch über das Runden hinaus gehen sowie mögliche Fehler beim Überschlagsrechnen thematisiert.
"Der Überschlag, der hilft eigentlich gar nicht..."
Im folgenden Video sehen Sie, was Viertklässler über das Überschlagsrechnen denken:
Bedeutung des Überschlagrechnens
In nichts zeigt sich der Mangel an mathematischer Bildung mehr als in einer übertrieben genauen Rechnung.
Carl Friedrich Gauß
Das Überschlagsrechnen kann, genau wie das Schätzen und Runden, der „Welt der ungenauen Zahlen" (vgl. Freudenthal 1978; Blankenagel 1983; Bönig 2003) zugeordnet werden und ist wichtiger Bestandteil der Grundschulmathematik.
Zum einen wird es mit zunehmendem Gebrauch von Taschenrechnern und Computern immer wichtiger, die damit gewonnenen Ergebnisse mit schnellen Größenabschätzungen auf ihre Richtigkeit hin zu überprüfen. Zum anderen sind genaue Rechnungen gar nicht immer nötig, sinnvoll oder gar möglich, was sich bereits im obigen Zitat von Gauß widerspiegelt und den Selbstzweck des Überschlags verdeutlicht.
So ergibt es beispielsweise nur wenig Sinn, seinen wöchentlichen Spritverbrauch genau ausrechnen zu wollen, weil dies von so vielen Faktoren abhängt, die eine genaue Rechnung kaum ermöglichen (vgl. van den Heuvel-Panhuizen 2001) und gleichzeitig für diesen Zweck auch viel zu umständlich wäre.
Eine weitere typische Situation, in der eine genaue Rechnung (im Kopf) viel zu umständlich wäre, ist das Berechnen von Rabatten, wie z.B. im Rahmen von Aktionen wie „20 % auf alles" in Kaufhäusern.
In der Regel reicht es hier vor dem Kauf eines Produkts zu wissen, ob die 20 % eher eine Ersparnis von vielleicht 5, 10 oder gar 30 Euro bringen, um den Endpreis mit anderen Anbietern vergleichen zu können. Doch obwohl viele Zahlen- und Größenabgaben in realen Anwendungssituationen zwangsläufig ungenau sind (z.B. Einwohnerzahlen), dominieren im Alltag des Mathematikunterrichts Präzision und Exaktheit (vgl. Bönig 2003, S. 102).
Darüber hinaus wird das Überschlagsrechnen nicht selten auf ein Rechnen mit gerundeten Zahlen unter Anwendung der konventionellen Rundungsregeln reduziert. Gleichzeitig wird es häufig nur in Verbindung mit den schriftlichen Rechenverfahren als Kontrollwerkzeug thematisiert.
Der Selbstzweck des Überschlagens bleibt zu oft Nebensache, mit der Folge, dass vielen Kindern die Bedeutung und der Nutzen des Überschlagens nicht bewusst werden und der Überschlag als lästige Zusatzrechnung empfunden wird (vgl. Bobrowski 1990), was teilweise auch in den Aussagen der Kinder im Einstiegsvideo ersichtlich wird („der Überschlag hilft eigentlich gar nicht").
Außerdem ist das Überschlagsrechnen eng verbunden mit einem „Zahlensinn". Auch wenn die Definitionen von Zahlensinn nicht immer einheitlich sind, so kann man allgemein darunter das Wissen über die Beziehung von Zahlen und den kritischen Umgang mit Zahlangaben verstehen (vgl. Lorenz 2005a, 2006).
Gute Fähigkeiten im Überschlagsrechnen sind dabei einerseits Indikator für Zahlensinn (Greeno 1991), zugleich wird ein guter Zahlensinn aber auch als Voraussetzung für das Überschlagsrechnen gesehen (Threadgill-Sowder 1984), so dass man hier von einer wechselseitigen Beziehung ausgehen kann.
Das Überschlagsrechnen spielt folglich eine wichtige Rolle für die mathematische Bildung und somit zur Erziehung der Schülerinnen und Schüler zum mündigen Bürger. Eine Möglichkeit den kritischen Blick auf Zahlen mithilfe von Überschlagsrechnungen zu schulen, liefert beispielsweise das Aufgabenformat „Kann das stimmen?". Ausgewählte Aufgabenbeispiele und Schülerbearbeitungen dazu finden Sie auf unserer Seite zur „Zeitungsmathematik".
Überschlagsrechnen - ein Prozess mit vielen Komponenten
Das Überschlagsrechnen stellt einen komplexen Prozess dar, der u.a. vom Aufgabentyp abhängig ist. Betrachtet man für die Grundschule typische Aufgaben zum Überschlagsrechnen, so kann man diese in sogenannte direkte und indirekte Überschlagsfragen unterteilen (vgl. van den Heuvel-Panhuizen 2001, S. 178).
Direkte Überschlagsfragen, zu denen insbesondere Aufgaben wie „Wie viel ist es ungefähr?" zählen, zeichnen sich dadurch aus, dass eine Zahl als Ergebnis verlangt ist, was das Anwenden einer formalen Überschlagsstrategie (vgl. Abschnitt 4) voraussetzt.
Indirekte Überschlagsfragen, zu denen man Aufgaben wie „Reicht das Geld?", „Ist es mehr oder weniger als...?" oder auch „Kann das stimmen?" zählen kann, erfordern hingegen nicht zwingend eine Zahl als Ergebnis. Dies ermöglicht auch ein globaleres Vorgehen - die Antwort auf die jeweilige Frage kann entweder mit einem formalen Überschlag oder aber mit einem informellen Überschlag (vgl. Abschnitt 4) bestimmt werden.
Wenn die Schülerinnen und Schüler eine Überschlagsrechnung nicht nur als das „Abspulen der Rundungsregeln" lernen sollen, ist es wichtig, dass sämtliche Komponenten des Überschlagsrechnens im Unterricht berücksichtigt werden. Dazu gehört z.B.
- das Wissen, wie man überschlägt/wie man die Vereinfachung durchführt,
- das Wissen darüber, welcher Vereinfachungsprozess zu einer leichten Rechnung führt (z.B. Runden oder Abbrechen),
- das Wissen über Kernideen des Überschlagsrechnens: z.B. Definitionen des Überschlagsrechnens, Auswirkungen des Überschlags (Überschlagsergebnis liegt über/unter genauem Ergebnis)
(vgl. z.B. LeFevre et al. 1993, van den Heuvel-Panhuizen 2001, Star et al. 2009). Darüber hinaus gilt insbesondere auch, dass die Kinder wissen müssen, dass ein formell bestimmtes Überschlagsergebnis bei indirekten Überschlagsfragen noch interpretiert werden muss, damit man eine sichere Antwort auf eine Frage wie z.B. „Reicht das Geld?" erhält. Dies wird bspw. an folgender Aufgabe deutlich:
„Du hast 70 € zum Geburtstag geschenkt bekommen. Reicht das Geld für vier T-Shirts, die je 16 € kosten?".
Wenn man diese Aufgabe durch Aufrunden des Geldbetrags auf Zehner überschlägt, erhält man als Lösung 4 ∙ 20 € = 80 €. Es scheint also zunächst als würde das Geld hier nicht reichen. An dieser Stelle muss man sich jedoch bewusst werden, dass viermal deutlich aufgerundet wurde, sodass das genaue Ergebnis unter dem Überschlagsergebnis liegt und es somit möglich ist, dass das Geld doch reichen könnte.
Eine genauere Rechnung oder eine Ausgleichsrechnung - also eine Interpretation - ist hier notwendig. Hier könnte man z.B. ausgleichen, indem man ausnutzt, dass das Ergebnis um 4 ∙ 4 € zu groß ist. Der entstandene Fehler ist folglich größer als 10 € und somit reichen die vorhandenen 70 € doch.
Überschlagsstrategien - Illustration und Analyse
Wie bereits mehrfach erwähnt, lässt sich das Überschlagsrechnen nicht auf die Anwendung der Rundungsregeln reduzieren. Vielmehr gibt es eine Fülle von Strategien. Bevor diese im Folgenden exemplarisch aufgezeigt werden sollen, machen Sie sich zunächst selbst Gedanken dazu.
Eigenaktivität
Finden Sie möglichst viele verschiedene Überschlagsrechnungen zu folgender Aufgabe:
23,52 + 22,99 + 24,36 ≈
Wie bereits in Abschnitt 3 angedeutet, können verschiedene Arten von Strategien - formell und informell (vgl. Hunke in Vorb.) beim Überschlagsrechnen ausgemacht werden, die im Folgenden illustriert werden sollen.
Formelle Überschlagsstrategien
Formellen Überschlagsstrategien ist im Wesentlichen gemeinsam, dass die Ausgangsaufgabe vereinfacht wird und dann mit der vereinfachten Aufgabe ‚genau‘ gerechnet wird. Je nach Aufgabe können unterschiedliche Strategien auch zur gleichen Überschlagsrechnung führen, was auch der Grund für mehrfach vorkommende Rechnungen in der folgenden Übersicht ist.
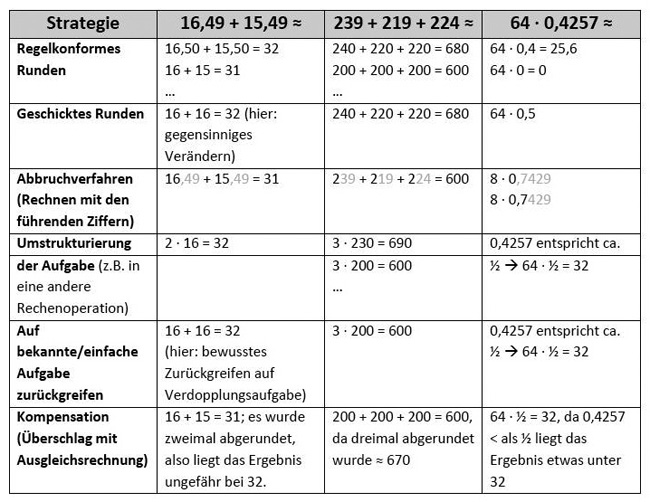
(Für eine größere Ansicht auf das Bild klicken)
Eigenaktivität
Videoanalyse
- Ordnen Sie das Vorgehen der Kinder in den folgenden Videos einer der o.g. Überschlagsstrategien zu.
- Gehen die Kinder eher regelgeleitet oder geschickt vor?
Felix
Guido
Samira
Lilli
Hier finden Sie mögliche Interpretationen zu den Videos im Hinblick auf die obigen Aufgabenstellungen:
Felix
Guido
Samira
Lilli
Informelle Überschlagsstrategien
Den oben dargestellten formellen Überschlagsstrategien ist gemeinsam, dass eine Aufgabe zunächst vereinfacht und diese vereinfachte Aufgabe dann quasi genau berechnet wird. Eine Untersuchung von Hunke (in Vorb.) konnte jedoch aufzeigen, dass es auch eine andere Art von Strategien, sogenannte informelle Überschlagsstrategien, gibt. Während die formellen Überschlagsstrategien sowohl bei direkten wie auch indirekten Überschlagsfragen beobachtet werden konnten, zeigten sich die informellen Strategien hauptsächlich bei der Lösung der indirekten Überschlagsfrage „Reicht das Geld?". Dies hängt mit dem Charakter dieses Aufgabentyps zusammen, da bei indirekten Überschlagsfragen, wie oben aufgezeigt, eine Zahl als Ergebnis nicht zwingend erforderlich ist.
1. Strategie: Genaue Rechnung wird abgebrochen, keine Zahl als Ergebnis
Beispiel:
Jonas
2. Strategie: Rechnung mit teilweise gerundeten Werten wird abgebrochen, keine Zahl als Ergebnis
Beispiel:
Sebastia
3. Strategie: Schätzen mit Bezug zur vorherigen Aufgabe
Beispiel:
Mehmet
Den informellen Überschlagsstrategien ist gemeinsam, dass das Ergebnis ab einer bestimmten Stelle im Lösungsprozess „gesehen“ wird, eine (zumeist genaue) Rechnung wird abgebrochen oder das Ergebnis wird aus einer vorherigen Aufgabe abgeleitet. Insgesamt sind diese Strategien vor allem alltagsnah und eng verbunden mit einem Zahlensinn, was durch Ausdrücke, wie „das Kleingedruckte“ (vgl. Sebastian) und „man kann das auch sehen“ (vgl. Jonas) deutlich wird.
Fehler
Wie oben erwähnt ist das Überschlagsrechnen ein komplexer Prozess und damit gehen nicht selten Fehler und Schwierigkeiten bei den Kindern einher. Schipper u.a. (2000) sehen die Ursachen vor allem in unzureichenden Vorkenntnissen. Insgesamt lassen sich drei Kategorien an Fehlern beim Überschlagsrechnen ausmachen (vgl. Hunke in Vorb.):
Überschlagsunabhängige Fehler
Darunter werden alldiejenigen Fehler verstanden, die bei der Durchführung einer Überschlagsrechnung unterlaufen, die aber ebenso bei der Durchführung einer analogen genauen Aufgabe gemacht worden wären. Dazu zählen z.B. Stellenwertfehler, Fehler mit der Null (zu viele/zu wenig Endnullen) oder reine Rechenfehler, wie im Beispiel von Guido, dem beim Ausrechnen seiner korrekt bestimmten Überschlagsaufgabe ein Fehler unterläuft:

(Für eine größere Ansicht auf das Bild klicken)
Rundungsfehler
Einigen Kindern scheint nicht bewusst, dass das Runden gemischter Geldbeträge auf glatte Einerbeträge bereits die Centbeträge mit einschließt. Deshalb runden sie erst die Eurobeträge, dann die Centbeträge und addieren die einzelnen Teilsummen, so wie die folgenden Beispiele von Derek aufzeigen:
16,49 € + 15,49 €
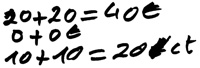
12,59 € + 14,95 €
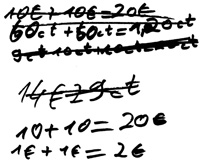
23,99 € + 24,49 € + 22,99 €
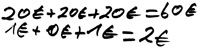
So rundet Derek bei der Aufgabe 16,49 € + 15,49 € zunächst die Eurobeträge regelkonform auf Zehner und erhält die Teilrechnung 20 + 20. Dann rundet er die Zehntelstellen auf Einer, was zur Teilrechnung 0 + 0 führt und dann rundet er außerdem noch die Hundertstel auf Zehntel und kommt so zu der Teilrechnung 10 ct + 10 ct = 20 ct, sodass er als Endergebnis 40,20 € erhält.
Dieser Fehler scheint eng verbunden mit der sogenannten „Komma-Trennt"-Strategie (vgl. Padberg 2009, S. 203). Nicht selten betrachten Kinder sowohl die Stellen vor, als auch nach dem Komma als natürliche Zahlen, was im vorliegenden Fall zu diesem „doppelten Runden" führt.
Kompensationsfehler
Wie bereits in Abschnitt 3 erwähnt, ist eine zentrale Komponente des Überschlagsrechnens das Wissen darüber, ob der Überschlag über oder unter dem genauen Ergebnis liegt. Einige Kinder stellen diese operativen Beziehungen von selbst her, was sich zumeist in der oben aufgeführten Überschlagsstrategie "Kompensation" widerspiegelt.
Auch ist es möglich, Kinder nach einer Überschlagsrechnung zu solch einer Kompensation aufzufordern. Der folgende Ausschnitt aus einem Interview mit Felix zeigt, dass die Kompensation nicht selten fehlerhaft erfolgt, aber gleichzeitig durchaus sinnvolle Denkwege der Kinder dahinterstecken:
Felix Kompensationsfehler
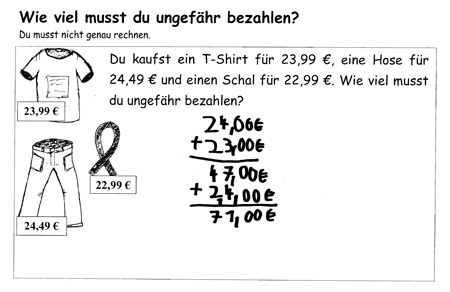
(Für eine größere Ansicht auf das Bild klicken)
Auf die Frage hin, ob das Überschlagsergebnis über oder unter dem genauen Ergebnis liege, kommt Felix zu dem Schluss, dass sein Überschlagsergebnis über dem genauen Ergebnis liege. Dazu liefert er folgende Begründung:
„Weil hier bei denen beiden, also bei dem Hemd und bei dem Schal...da musste ich beide Aufgaben..höher - also höher machen, aber hier (zeigt auf die Hose) nur tiefer. Also hab ich herausgefunden, dass hier, das sind ja hier zwei Sachen und das nur eine."
An Felix Vorgehensweise fällt auf dass ihm bereits bewusst ist, dass er die operativen Beziehungen herstellen kann, indem er die Auswirkungen des Rundens analysiert und dass eine genaue Rechnung (die man dann mit dem Überschlag vergleichen kann) nicht nötig ist. Diese operativen Beziehungen stellt er jedoch auf individuelle Weise her.
So zieht er hier nicht in Betracht, wie stark er die einzelnen Summanden gerundet hat, sondern wie viele Summanden er jeweils auf- bzw. abgerundet hat, was zu der aus Erwachsenensicht falschen Annahme führt, dass sein Überschlag über dem genauen Ergebnis liege, weil er ja zweimal aufgerundet und nur einmal abgerundet habe.
Ihm scheint an dieser Stelle noch nicht bewusst, dass sich der durch das Abrunden um 49 Cent entstandene Fehler stärker auf das Überschlagsergebnis auswirkt als das zweimalige Aufrunden um je 1 Cent.
Felix' Kompensationsfehler ist nur ein Beispiel für mögliche Schwierigkeiten bei der Kompensation. So gibt es bei der Kompensation nicht den Fehler, sondern Fehler zeigen sich in vielfältiger Form. Im folgenden Video sehen Sie deshalb Ausschnitte aus einem Interview mit Angela, die einen anderen Fehler macht als Felix.
Eigenaktivität
Betrachten Sie das Video und beschreiben Sie Angelas Fehler.
Angelas Kompensationsfehler
Hier finden Sie eine mögliche Interpretation des Fehlers:
Analysevorschlag: Angelas Kompensationsfehler
Konsequenzen für den Unterricht
Wie eingangs aufgezeigt ist es wichtig, das Überschlagsrechnen nicht zu eng an die Rundungsregeln und an die schriftlichen Rechenverfahren zu koppeln, sondern es in seiner gesamten Bedeutung zu thematisieren. In diesem Zusammenhang erscheint die Einbettung in geeignete Sachkontexte einerseits und eine methodische Umsetzung im Sinne des flexiblen Rechnens andererseits sinnvoll.
Dabei sollte es aber nicht Ziel des Unterrichts sein, dass die Kinder ein Repertoire an vorgefertigten Strategien beherrschen und abrufen können sollten. Im Sinne des flexiblen Rechnens geht es vielmehr darum, dass die Kinder ausgehend von der jeweiligen Aufgabe geschickt die Zahlbeziehungen ausnutzen und darauf basierend eine geeignete ungefähre Rechnung durchführen, aber ebenso reflektiert entscheiden, ob eine genaue oder eine ungefähre Rechnung sinnvoller ist (vgl. z.B. Laferi 2009).
In diesem Zusammenhang können beispielsweise Arbeitsaufträge wie „Welche Aufgaben rechnest du genau, welche mit einem Überschlag? Warum?" gestellt werden. Auch erscheinen Aufgaben wie „Finde möglichst viele verschiedene Überschlagsrechnungen zu dieser Aufgabe" sinnvoll. So kann den Kindern bewusst werden, dass es nicht die richtige Überschlagsrechnung und nicht das richtige Ergebnis gibt, sondern dass das Ergebnis gerade beim Überschlagsrechnen in einem gewissen Rahmen offen ist.
Die auf dieser Seite aufgezeigten Besonderheiten indirekter Überschlagsfragen führen darüber hinaus zu der Forderung nach einem gezielteren Einsatz solcher Aufgabenformate. Insbesondere Aufgaben wie "Reicht es?" erscheinen geeignet, um ein Nachdenken über die Auswirkungen des Rundens und die Notwendigkeit über das Bestimmen dieser Auswirkungen anzuregen.
Im Hinblick auf die vielfältigen Fehler (vgl. Abschnitt 5) ist es schließlich außerdem wichtig, mit den Kindern vor allem über Rundungs- und Kompensationsfehler zu sprechen, damit sie ihre individuellen Strategien mehr und mehr den „richtigen" Strategien annähern können. Ein kompetenzorientierter Umgang mit den Schülerfehlern ist dabei auch beim Überschlagsrechnen nicht zu vernachlässigen.
Verwandte Themen
Zeitungsmathematik
Die Bauernhofaufgabe
Stützpunktvorstellungen
Begriffsklärung: Schätzen - Runden - Überschlagen
Die Begriffe Schätzen, Runden und Überschlagen sind eng miteinander verbunden und gerade Schätzen und Überschlagen werden nicht selten synonym gebraucht. Diese Seite orientiert sich dabei an der von Lorenz (2005b) vorgenommenen Unterscheidung. Lorenz versteht unter Überschlagsrechnen „das Ergebnis einer arithmetischen Operation ungefähr, das heißt, mit einer gewissen Näherung, aber damit durchaus auch mit einem einkalkulierten Fehler zu bestimmen" (Lorenz 2005b, S. 44). Weitere Informationen dazu finden Sie in:
Lorenz, J. H. (2005b). Überschlagen - Schätzen - Runden. Drei Begriffe, eine Tätigkeit? Grundschule Mathematik, (4), 44-45.
Hier finden Sie einen kurzen Überblick zum Schätzen.
Konkrete Unterrichtsideen zum Überschlagsrechnen finden sich z.B. in
Selter, Ch. (1999). Geschickt rechnen - schätzend rechnen. Die Grundschulzeitschrift, 125, 23-38.
...und in...
Grundschule Mathematik. H. 4/2005. Rechnen: Überschlagen.
Inwiefern Kinder des vierten Schuljahres die in Abschnitt 3 angesprochene Interpretation von Überschlagsergebnissen vornehmen, können Sie im folgenden Aufsatz erfahren:
Hunke, S. (2011). „Reicht das Geld?" - wie Viertklässler Überschlagsergebnisse interpretieren. Beiträge zum Mathematikunterricht.
Wie den Kindern im Unterricht nahe gebracht werden kann, wozu und wann eine Überschlagsrechnung sinnvoll gebraucht werden kann, erfahren Sie auf primakom: Inhalte: Zahlen und Operationen.
Literatur