Auf dieser Seite erhalten Sie die Möglichkeit, sich mit Vorgehensweisen von Grundschülern bei Aufgaben zur halbschriftlichen Subtraktion auseinanderzusetzen. Anhand von Schülerdokumenten und Videos werden Einblicke in die Vorgehensweisen von Schülerinnen und Schülern gegeben und charakteristische Schwierigkeiten näher betrachtet.
Moritz rechnet 34198 - 17210
Der Drittklässler Moritz sollte zu Beginn des Schuljahres die Aufgabe 34198 - 17210 lösen. Zu diesem Zeitpunkt lernte er gerade den Zahlenraum bis 1000 kennen, das Verfahren der schriftlichen Subtraktion war ihm noch nicht bekannt und ein Taschenrechner stand ihm ebenfalls nicht zur Verfügung.
Eigenaktivität
Schauen Sie sich an wie Moritz rechnet und überlegen Sie, was das Besondere an seiner Vorgehensweise ist.
Moritz
Hier können Sie nachlesen, was dieses Beispiel verdeutlichen soll.
Hintergrundwissen zur halbschriftlichen Subtraktion
Das zentrale Kennzeichen des halbschriftlichen Rechnens ist genau diese Zerlegung von komplizierten Aufgaben in leichtere Teilaufgaben. Dabei werden, wie Moritz es zeigt, einzelne Rechenschritte sowie Teilergebnisse notiert, bis am Schluss das Ergebnis ermittelt ist (vgl. Wittmann & Müller 1993, S. 85). Das halbschriftliche Rechnen zeichnet sich durch folgende Charakteristika aus:
- Die Rechenwege sind beim halbschriftlichen Rechnen im Gegensatz zu den schriftlichen Algorithmen nicht vorgegeben.
- Die Notationsweise ist nicht festgelegt. Die Kinder notieren nicht unbedingt alle Teilschritte.
- Welche Lösungsstrategie aus der Sicht geübter Rechner sinnvoll oder weniger sinnvoll ist, hängt von den Zahlenwerten der jeweiligen Aufgabe ab.
Typische Vorgehensweisen bei der halbschriftlichen Subtraktion
Auch wenn verschiedene Kinder die gleiche Strategie einschlagen, kann man trotzdem immer individuelle Unterschiede in der Durchführung bzw. Anwendung und Notation der jeweiligen Strategie erkennen.
Im Folgenden sehen Sie drei Kinder, die alle versuchen mit der Strategie "Stellenweise" die ihnen vorgelegte Aufgabe zu lösen. Die dahinter liegenden individuellen Denkweisen der Kinder sollen dadurch verdeutlicht werden.
Eigenaktivität
Schauen Sie sich zunächst die Dokumente und dann die Videos an. Überlegen Sie, worin die Unterschiede im Vorgehen der Kinder innerhalb der Strategie "Stellenweise" bestehen.

Mourice, 3. Klasse
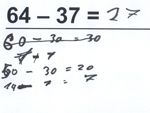
Florian, 4. Klasse
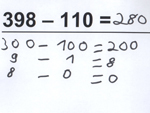
Melissa, 3. Klasse
Was ist das Besondere an dem jeweiligen Vorgehen der Kinder?
Hier finden Sie eine mögliche Analyse der unterschiedlichen Vorgehensweisen.
Bei einer Untersuchung von Selter (2000) zu den Vorgehensweisen von Grundschülerinnen und Grundschülern bei Aufgaben zur Addition und Subtraktion im Zahlenraum bis 1000, stellte sich heraus, dass die Mehrzahl der Kinder unabhängig von den Zahlenwerten die Rechenstrategien "Schrittweise" und "Stellenweise" nutzten, obwohl ihnen der Rechenweg freigestellt war.
Zudem stellte sich heraus, dass die Kinder oftmals bei der Berechnung verschiedener Aufgaben eine Hauptstrategie beibehielten und nicht aufgabenabhängig die Strategie wechselten.
Im Unterricht sollte durch entsprechende, auch materialgestütze Thematisierung einzelner Strategien und ihren aufgabenbezogenen Einsatz wenig flexibler Nutzung entgegengewirkt werden.
Typische Fehler bei der halbschriftlichen Subtraktion
Beim halbschriftlichen Lösen von Subtraktionsaufgaben treten, ähnlich wie bei der halbschiftlichen Addition, manche Fehler vermehrt auf.
Meseth & Selter (2002, S. 55 ff.) kategorisierten in ihrer Studie sogenannte "typischen Fehler". Dabei muss in diagnostischen Prozessen unterschieden werden, inwiefern es sich um Merk-, Rechen- oder Verständnisfehler handelt.
Denn je nach Art des Fehlers und den dahinterliegenden (fehlerhaften) Vorstellungen, müssen diese unterschiedlich aufgearbeitet werden. Auch der Bezug zu bestimmten Strategien kann festgestellt werden. So treten gewisse Fehler z.B. hauptsächlich beim Ausgleich einer Hilfsaufgabe aus.
Die folgende Beispiele sollen dafür einen ersten Einblick gewähren.
1. Verständnisfehler - Anwendung der Umkehroperation bei der Verknüpfung der Zwischenergebnisse
Die Ergebnisse der Teilrechnungen werden nach der halbschriftlichen Strategie ,,Stellenweise'' korrekt berechnet. Allerdings werden sie anschließend nicht addiert, sondern subtrahiert. Durch die falsche Verknüpfung der Zwischenergebnisse wird eine falsche Differenz ermittelt.
Beispiel
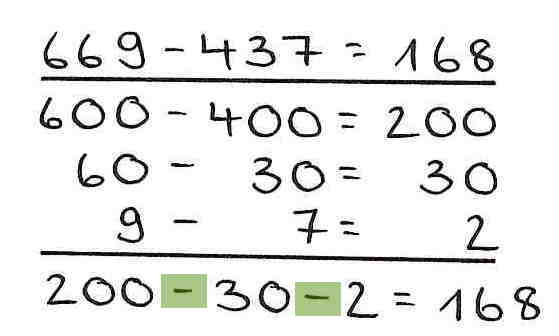
2. Verständnisfehler - gegensinniges Verändern von Minuend und Subtrahend
In diesem Beispiel wird das Gesetz von der Konstanz der Differenz falsch angewendet. Anstatt gleichsinnig zu verändern, wird hier fälschlicherweise gegensinnig verändert (773 - 1 und 299 + 1).
Beispiel:
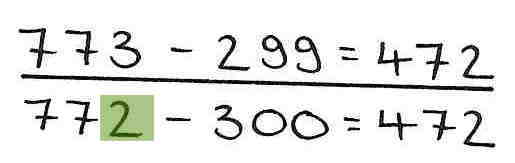
3. Rechenfehler - Vernachlässigung von Teilrechnungen
Es werden zwar alle Teilrechnungen notiert, aber nicht ausgeführt. Beispielsweise werden nur die Einer (8) subtrahiert, die Zehner (70) bleiben unberücksichtigt.
Beispiel:
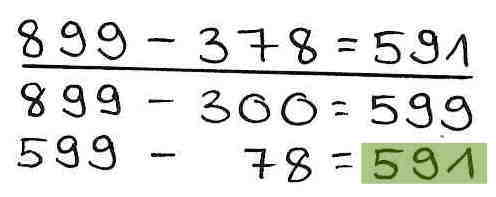
4. Rechenfehler - Vernachlässigung der Stellenwerte
Bei der Ermittlung des Zwischenergebnisses der ersten Teilrechnung wird anstatt 400 40 notiert und anschließend verrechnet. Der Fehler liegt also entweder im Stellenwertverständnis oder in einer flüchtigen Notation.
Beispiel:
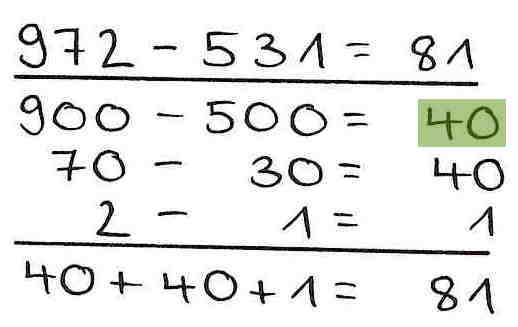
5. Merkfehler
Obwohl die einzelnen Rechnungen korrekt sind, wird in diesem Beispiel ein anderer Wert als der des Zwischenergebnisses notiert und verrechnet (statt 463 436).
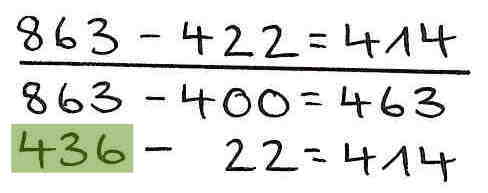
Eigenaktivität
Erkennen Sie die Fehler? Überlegen Sie auch zunächst selbst, was hinter diesen fehlerhaften Vorgehensweisen stecken könnte.
845 - 399 = 554
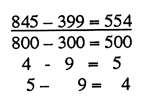
701 - 698 = 1
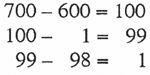
701 - 698 = 97
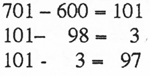
Wie sind diese fehlerhaften Lösungen vielleicht entstanden?
Hier finden Sie eine kompetenzorientierte Erklärung der Rechenfehler.
Das KIRA-Quiz
Beim KIRA-Quiz können Sie weiterhin testen, wie gut Sie sich schon in das mathematische Denken von Kindern bei der halbschriftlichen Subtraktion hineinversetzen können. Wir haben Kinder die Subtraktionsaufgaben 62-39 sowie 53-28 rechnen lassen. Auf den QUIZ Seiten finden Sie zehn unterschiedliche Schülerlösungen für diese Aufgaben und Sie können versuchen, selbst herauszufinden, wie die Kinder gerechnet haben.
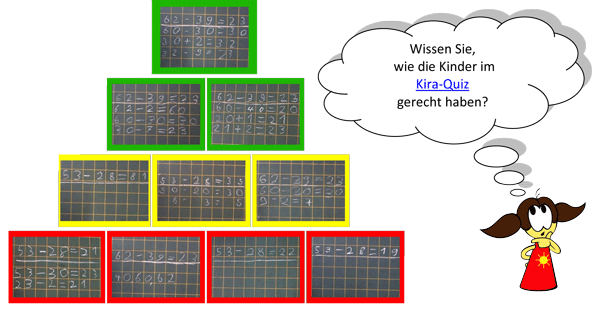
Testen Sie Ihr Wissen zu dem Thema in unserem Kira-Check.
Verwandte Themen
Halbschriftliche Addition
Hier finden Sie weitere Kinderdokumente zur Analyse aus einer Bachelorarbeit zur halbschriftlichen Subtraktion. In dieser Arbeit wurde untersucht, ob es mögliche Einflussfaktoren auf die Wahl der Strategie gibt. Hierzu wurden gezielt die Einflussfaktoren "mit oder ohne Kontextbezug" und "bekannter oder unbekannter Zahlenraum" betrachtet. Zudem wurde die Fehleranfälligkeit einzelner Strategien analysiert.
Materialien zum Thema 'Rechnen auf eigenen Wegen' sowie 'Vom halbschriftlichen zum schriftlichen Rechnen' finden Sie auf der Website des Projekts PIK AS im PIKAS: Fortbildungsmodul: 'Lernen auf eigenen Wegen' .
Die meisten Erwachsenen kennen aus der Schule entweder nur die schriftlichen Rechenverfahren oder nutzen im Alltag intuitiv halbschriftliche Vorgehensweisen. Als Lehrperson mit dem Fach Mathematik sollten Sie allerdings die große Vielfalt halbschriftlicher Rechenverfahren kennen und im Unterricht mit Blick auf die individuellen Vorlieben der Lernenden die eine oder andere Strategie thematisieren. Kompakte Hintergrundinformationen sowie unterrichtspraktische Hinweise zu den halbschriftlichen Rechenstrategien finden Sie primakom: Inhalte: Zahlen und Operationen: Halbschriftliches Rechnen: Einstieg.
Literatur
