Wie gehen Kinder mit ungewohnten Darstellungen von Zahlen in der Stellenwerttafel um? Wie werden Zahlen, die mit Hilfe von Anschauungsmaterialien dargestellt sind, von Kindern interpretiert? Welche Strategien haben Kinder beim Bündeln und Entbündeln von Zahlen entwickelt?
Mit Hilfe einer Standortbestimmung zum Stellenwertsystem, die auf Basis von Akinwunmi, Deutscher & Mosandl (2014) entstanden ist, werden diese Fragen hier exemplarisch beantwortet und Lösungswege von Kindern der dritten und vierten Klasse vorgestellt. Dabei werden Sie als Leserin oder Leser auch angeregt, über Ihre eigenen Erfahrungen und Vorstellungen mit dem Stellenwertsystem zu reflektieren.
1. 37 Zehner in der Stellenwerttafel?
 |
Tragen Sie in die Stellentafel 3 Tausender, 5 Hunderter, 37 Zehner und 9 Einer ein. Erklären Sie Ihre Lösung.
|
|
Mit solchen nicht standardisierten Zahldarstellungen in der Stellentafel werden die gewohnten Strukturen der Stellenwerte aufgehoben und das Verständnis der Zahlendarstellung in der Stellentafel angesprochen. Wie sind Sie bei der ungewohnten Darstellung vorgegangen, als Sie versucht haben, die Zahlen in die Stellentafel zu übertragen? Versuchen Sie, Ihre Erklärung in einem Satz festzuhalten. In Kapitel 3 können Sie Lösungsvorschläge verschiedener Kinder ansehen.
2. Das dezimale Stellenwertsystem
Das dezimale Stellenwertsystem respektive das dekadische Stellenwertsystem setzt sich aus Zehnerpotenzen zusammen. Jede Zahl kann durch Multiplikation und Addition von den entsprechenden Zehnerpotenzen dargestellt werden. Die Zahl 235 entspricht etwa 2*10² + 3*10¹ + 5*10⁰ = 2*100 + 3*10 + 5*1. Im Gegensatz zu anderen Systemen, wie etwa dem römischen Stellenwertsystem, können mit dem dezimalen Stellenwertsystem alle Zahlen mit Hilfe der zehn Ziffern von 0 bis 9 dargestellt werden.
An der angeführten exemplarischen Zahldarstellung der 235 lassen sich zwei zentrale Eigenschaften des dezimalen Stellenwertsystems ablesen:
„1. Die Ziffer gibt uns die Anzahl der Bündel der betreffenden Mächtigkeit an (Zahlenwert der Ziffer).
2. Die Stellung der Ziffer innerhalb des Zahlwortes gibt die Mächtigkeit des zugehörigen Bündels an (Stellenwert der Ziffer)“ (Padberg & Benz 2011, 82).
Übertragen auf die oben angeführte Zahldarstellung der 235 bedeutet dies Folgendes: Die einzelnen Ziffern der Zahl (zwei, drei und fünf) stellen jeweils die Anzahl der Bündel dar und sind demnach in der oberen Rechnung der erste Faktor. Die Position der Ziffern bedingt den zweiten Faktor, der aus einer Zehnerpotenz besteht, wobei die Mächtigkeit der Zehnerpotenz von der jeweiligen Stelle abhängig ist. Das Kriterium Stellenwert der Ziffer bedeutet, dass Ziffern je nach Position unterschiedliche Mächtigkeiten ausdrücken. So entspricht die Ziffer 5 in der Zahl 5432 einer anderen Mächtigkeit als in der Zahl 65 (Padberg & Büchter 2015, 29).
Die Ziffer Null hat im dezimalen Stellenwertsystem eine zentrale Rolle.
3. Bündeln und entbündeln
Bündeln bezeichnet „Elemente einer vorgegebenen Menge (z. B. eine große Anzahl Tischtennisbälle) zu gleich großen (»gleichmächtigen«) Gruppierungen zusammenzufassen“ (Krauthausen & Scherer 2007, 17). Im dekadischen Stellenwertsystem bestehen Bündel bzw. die gleichmächtigen Gruppierungen aus 10 Einheiten. Kinder der dritten und vierten Klasse wurden auch mit unüblichen Darstellungen des Dienes-Materials konfrontiert.
 |
1. Überlegen Sie kurz, welche Zahlen mit den Materialien dargestellt werden.
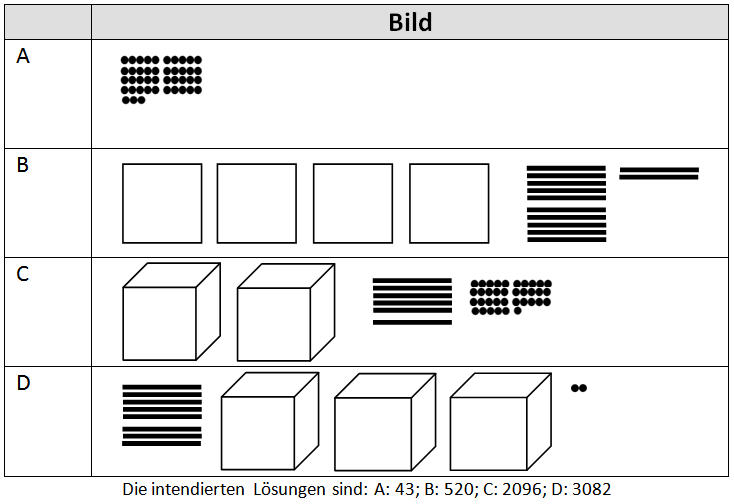
2. Wie gelangen die Kinder zu den Ergebnissen? Welche potentiellen Schwierigkeiten können Sie erkennen? |
|
| A |
 |
Hier werden möglicherweise die Fünferbündel als Zehner interpretiert. |
 |
Hier werden möglicherweise ebenfalls die Fünferbündel als Zehner interpretiert, wobei ein Minus-eins-Fehler unterläuft. |
 |
Entweder unterläuft dem Kind hierbei ein Zahlendreher oder Zehner und Einer werden umgekehrt interpretiert. |
 |
Die Anschauungsmittel werden verwendet, um eine den Konventionen entsprechende Darstellung der Zahlen zu präsentieren. Hierbei wird allerdings eine Zehnerstange nicht eingezeichnet. |
| B |
 |
Die 10 Zehnerstangen werden zu einem Hunderter gebündelt und mit den zwei einzelnen Zehnern addiert. Allerdings werden die vier Hunderter als Tausender interpretiert oder der Zahl 4 wird eine eigene Stelle zugeschrieben, weil der entstandene Hunderter (10 Zehner) nicht als solcher interpretiert wird. Es ist ersichtlich, dass dem Kind die Bedeutung der 10 als Bündelungseinheit bekannt ist. |
 |
Ähnlich wie in der Interpretation der vorherigen Abbildung werden hier die 12 Zehner nicht zu einem Hunderter und 2 Zehnern gebündelt, sondern die Ziffern jeweils stellenweise aufgeschrieben, wobei nicht auf den korrekten Stellenwert geachtet wird.
Es ist ersichtlich, dass dem Kind die Bedeutung der 10 als Bündelungseinheit bekannt ist. |
 |
Die Anschauungsmittel werden verwendet, um eine den Konventionen entsprechende Darstellung der Zahlen zu präsentieren. |
| C |
 |
Die 36 Einer werden erkannt, allerdings nicht zu 3 Zehnern gebündelt und zu den 6 übrigen Zehnern addiert, wodurch die 6 Zehner an die Hunderterstelle geschrieben werden. Da keine Hunderter abgebildet oder gebündelt werden können, wird eine Null für das Nichtvorhandensein eingefügt und die Ziffer 2 für die Tausender (bzw. Zehntausender) notiert. Das Kind setzt die Symbole als Einheit in Zahlen um. ‚Nicht vorhandene’ Stellen werden mit einer Null gekennzeichnet. |
 |
Ähnlich wie in der vorherigen Abbildung werden die gleichen Symbole als Einheit verstanden und die entsprechenden Ziffern hintereinander geschrieben. Vermutlich werden die Fünferbündel als Zehner interpretiert, weshalb ein Einer übrig bleibt und insgesamt 7 Zehner notiert werden. |
 |
Die Anschauungsmittel werden verwendet, um eine den Konventionen entsprechende Darstellung der Zahlen zu präsentieren. |
| D |
 |
Die Stellen werden in der Reihenfolge der Zeichnungen interpretiert, wobei die symbolische Bedeutung (möglicherweise zufällig) nur bei den Einern beachtet wird. |
 |
Durch das Fehlen der Hunderter und das Nichtkennzeichnen dieses Stellenwertes mit einer Null wird das Endergebnis um diese Stelle gekürzt. So entspricht die Darstellung in der Stellentafel nicht der endgültigen Zahl. Die Null als Ziffer im Stellenwertsystem sollte hier noch einmal thematisiert werden. |
4. Umgang mit ungewohnten Darstellungen im Stellenwertsystem
Im ersten Kapitel haben Sie die Aufgabe bearbeitet, die auch Kindern der dritten und vierten Klasse gestellt wurde. Nachdem Sie einen kurzen theoretischen Überblick über das Stellenwertsystem bekommen haben, können Sie hier Ihre Lösung zur Einstiegsaufgabe mit denen der Kinder vergleichen.
 |
1. Versuchen Sie, die jeweilige Erklärung der Kinder nachzuvollziehen.
2. Versuchen Sie, aus den Ergebnissen mögliche Förderungsbedarfe abzuleiten. |
|
Die folgende Aufgabe wurde von den Kindern bearbeitet und schriftlich erläutert:
Erkläre deine Lösung zur Aufgabe 3 T, 5 H, 37 Z, 9 E.
| Erklärung des Kindes |
Darstellung der Zahl in der Stellentafel |
| Ole: „Ich wusste, eine Stange ist 10 Einer. Dann habe ich das 37 Mal gerechnet.“ |
|
| Clara: „3 T sind klar, 5H + 37 Z = 870.“ |
|
| Sam: „Ich habe von der 37 die 30 Zehner weggenommen, um 3 Hunderter dazu zu holen.“ |
|
| Mia:„Ich habe Einer + Einer gerechnet. Dann war daraus 16 gekommen und dann habe ich den Zehner auch dazugetan. Dann habe ich das Ergebnis herausgefunden.“ |
|
| Dominik: „Ich habe 37 + 9 = 46 gerechnet. Dann habe ich 6 zu den Einern getan und dann habe ich die 4 zu den Zehnern getan.“ |
|
| Kim: „Ich habe sie aufgeschrieben und die Zahl war 35379.“ |
|
| Tanja: „Die Zahlen, die über 9 sind die habe ich einfach in zwei Kästchen geschrieben.“ |
|
 |
Hier finden Sie Interpretationsvorschläge zu den einzelnen Lösungsvorschlägen der Kinder hinsichtlich der Fragestellungen. |
|
5. Anschauungsmittel und Rechnen an der Stellenwerttafel
Eine Möglichkeit, das Verständnis der dekadischen Struktur des Stellenwertsystems aufzubauen, kann mit Hilfe des sog. Dienes-Materials erfolgen. Dieses besteht aus Einerwürfeln, Zehnerstangen, Hunderterplatten und Tausenderwürfeln.
Das Dienes-Material bietet den Kindern die Möglichkeit, die Struktur der Stellenwerte zu durchdringen und mentale Bilder aufzubauen. Schauen Sie sich die Ergebnisse und die bildliche Darstellung der Rechenoperationen (Addition und Subtraktion) an.
 |
1. Versuchen Sie, den jeweiligen Rechenweg der Kinder nachzuvollziehen.
2. Welche Chancen und Risiken birgt das Anschauungsmaterial bei der Bearbeitung dieser Aufgaben? |
|
5.1 Addition mit Anschauungsmaterial
Folgende Aufgabe bekamen die Kinder gestellt: Zu der Zahl 246 kommen 4 Zehner dazu. Welche Zahl ist es jetzt? Zeichne sie, trage sie in die Stellentafel ein und schreibe sie auf.
Kira

Anna

Tim

Niko

Jenny

Damian

 |
Hier finden Sie Interpretationsvorschläge zu den einzelnen Lösungsvorschlägen der Kinder hinsichtlich der Fragestellungen. |
|
5.2 Subtraktion mit Anschauungsmaterial
Die folgende Aufgabe wurde den Kindern im Rahmen der Subtraktion mit Anschauungsmaterial gestellt: Von der Zahl 514 werden 3 Zehner weggenommen. Welche Zahl ist es jetzt? Zeichne sie, trage sie in die Stellentafel ein und schreibe sie auf.
Britta

Chris

Ben

Lisa

 |
Hier finden Sie Interpretationsvorschläge zu den einzelnen Lösungsvorschlägen der Kinder hinsichtlich der Fragestellungen. |
|
6. Verwandte Themen
Orientierung im Hunderterraum
Hintergrundinformationen zur Entwicklung des Stellenwertverständnisses, typische Fehler und Unterstützungsmaßnahmen für den Unterricht finden Sie
hier.
7. Verwendetes Material
Die verwendete Standortbestimmung wurde in Anlehnung an Akinwunmi, Deutscher & Mosandl (2014) erstellt. Auszüge der Originalmaterialien sind unter folgendem Link unter den Materialien zum Förderbaustein N1 – Stellenwerte verstehen zu finden: http://mathe-sicher-koennen.dzlm.de/002.
8. Literatur
Diese Seite wurde erstellt von Beatrice Dürdodt für das Projekt Kira.