Die Multiplikation stellt eine der vier Grundrechenarten der Mathematik dar.
Hier sollen Beispiele für die Bearbeitung von unterschiedlichen Aufgabenformaten dieser Grundrechenarten präsentiert werden. Die beschriebenen Aufgaben wurden von Kindern der zweiten und dritten Klasse bearbeitet und sind in Anlehnung an eine Standortbestimmung zur Multiplikation von Akinwunmi, Deutscher & Mosandl (2014) konzipiert.
Alle Kinder hatten im schulischen Kontext bereits Kontakt zu Multiplikationsaufgaben, sodass es sich hier um eine Standortbestimmung der Lösungsstrategien zu dieser Grundrechenart handelt.
Auf dieser Seite soll die Vielfältigkeit möglicher Herangehensweisen an Multiplikationsaufgaben präsentiert werden und den Leserinnen und Lesern die Möglichkeit geboten werden, das Operationsverständnis der Kinder zu analysieren.
Multiplikation und Würfel
Eigenaktivität
Betrachten Sie die Schülerlösungen zur Aufgabe "Zeichne ein Würfelbild, das zur Aufgabe 5 · 2 = 10 passt". Welche Kompetenzen zeigen die Kinder und wo entdecken Sie potentielle Schwierigkeiten?

Ani
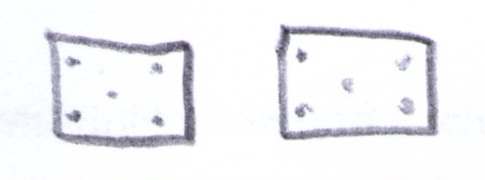
Lin
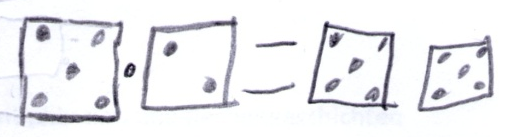
Tom

Claas
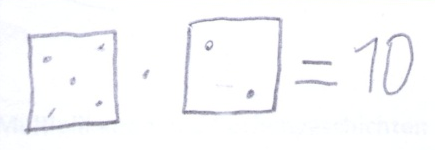
Saeed
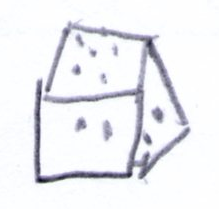
Emma
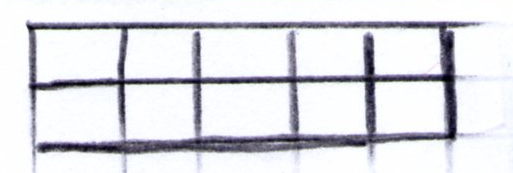
Talea

Kim
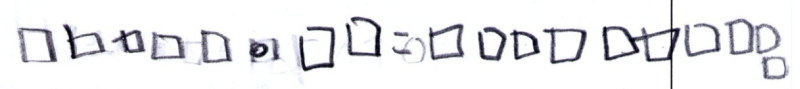
Dominik
2. Grundvorstellungen der Multiplikation
In diesem Abschnitt sollen die Grundvorstellungen der Multiplikation in kurzer und prägnanter Form vorgestellt werden. Bei der Multiplikation können drei Grundvorstellungen unterschieden werden (Padberg & Benz 2011, S. 128-131): zeitlich-sukzessive Handlungen, räumlich-simultane Anordnungen und kombinatorischer Kontext.
Zeitlich-sukzessive Handlungen

Dieses Bild soll die zeitlich-sukzessive Handlung der Multiplikation verdeutlichen. Schrittweise (sukzessiv) wird durch die Wiederholung einer Handlung (vier Mal drei Luftballons aufhängen) das Produkt erreicht. Der Zusammenhang zur schrittweisen Addition wird bei dieser Grundvorstellung sehr deutlich (Padberg & Benz 2011, S. 129). Entstandene Rechengeschichten zu diesem Bild finden Sie in Kapitel 4.
Räumlich-simultane Anordnung
Eine Schokoladentafel repräsentiert die räumlich-simultane Grundvorstellung der Multiplikation. Diese Darstellungsform ist zum Beispiel hinsichtlich der Erklärung von Rechengesetzen, wie des Kommutativgesetzes, hilfreich (Akinwunmi, Deutscher & Selter 2014, 78). Das gesamte Produkt ist an der Darstellung abzulesen, da es möglich ist, die Anzahl aufgrund der räumlichen Anordnung zu erfassen. Auch hier ist eine wiederholte Addition als Lösungsstrategie zur Errechnung des Produktes möglich.
Die beiden erstgenannten Grundvorstellungen sind eng miteinander verknüpft. So ist das Endprodukt einer zeitlich-sukzessiven Handlung eine räumlich-simultane Anordnung und umgekehrt kann eine solche Anordnung in eine zeitlich-sukzessive Handlung umgewandelt werden (Padberg & Benz 2011, S. 130).
Kombinatorischer Kontext
Einen weiteren Zugang zur Multiplikation stellt die Kombinatorik dar. Eine klassische Aufgabenstellung für diese Grundvorstellung ist zum Beispiel: „Wie viele Menüs kann ein Mensch zusammenstellen, der aus drei Vorspeisen, zwei Hauptmenüs und drei Nachspeisen wählen kann?“ Graphisch ließe sich die Aufgabe wie in der untenstehenden Abbildung lösen. Die dazugehörige Multiplikation würde 3 · 2 · 3 = 18 lauten.

Im Gegensatz zu den anderen beiden Grundvorstellungen weist dieser Zugang diverse Nachteile auf, zum Beispiel in Hinblick auf den nicht direkt ersichtlichen Zusammenhang zur Division. Weiterhin ist er durch einen engen Anwendungsbezug und eine geringe Möglichkeit der Verwendung von Anschauungsmitteln begrenzt, weshalb Padberg und Benz (2011, S. 130) zu dem Schluss kommen, dass dieser Zugang nicht unbedingt zur Einführung in diese Grundrechenart verwendet werden sollte.
Dies bedeutet allerdings nicht, dass er als Teil der unterrichtlichen Praxis ausgeschlossen, sondern im weiteren Verlauf der Multiplikation thematisiert werden sollte.
Vorstellung von Multiplikationsaufgaben am Zahlenstrahl
Eigenaktivität
- Lösen Sie zunächst die Multiplikationsaufgaben am Zahlenstrahl.
- Versuchen Sie daraufhin, die Lösungen der Kinder nachzuvollziehen. Können Sie dabei Chancen und Schwierigkeiten feststellen, die mit dem Zahlenstrahl als Anschauungsmittel verbunden sind?
1) Schreiben Sie zu dem Zahlenstrahl-Bild eine passende Aufgabe auf.
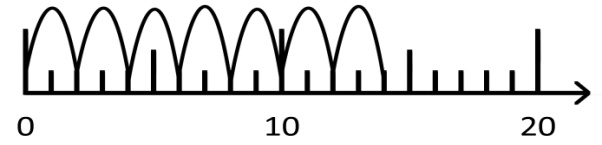
2) Zeichnen Sie zu der Mal-Aufgabe 6 · 3 ein passendes Bild in den Zahlenstrahl:
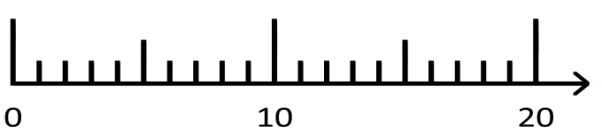
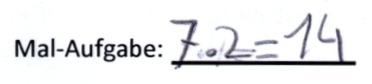
Clark
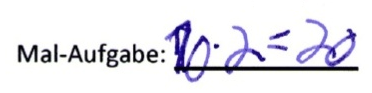
Mira
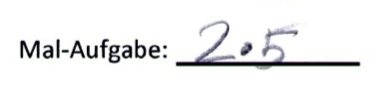
Annabel
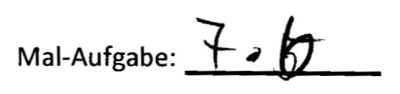
Jassin
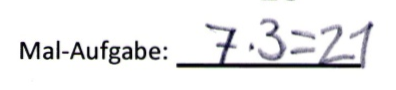
Luca
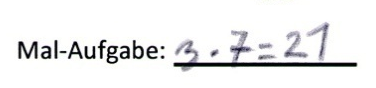
Christin
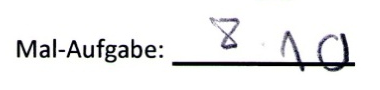
Julie
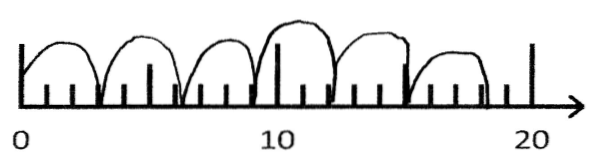
Marvin
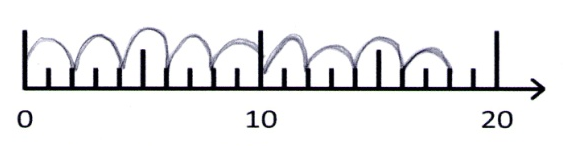
Lioba
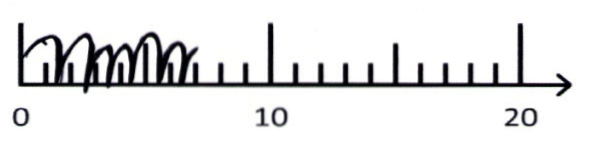
Tim
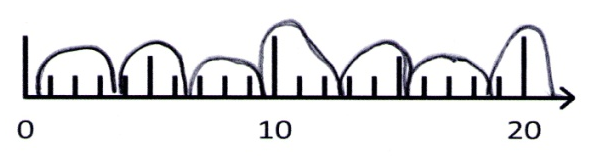
Dana
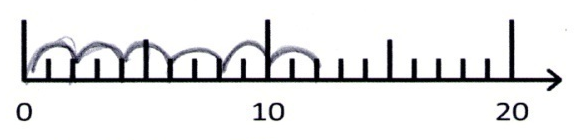
Theresa
Hier finden Sie Interpretationsvorschläge zu den einzelnen Lösungen der Kinder hinsichtlich der Fragestellungen.
Theoretisch bietet der Zahlenstrahl ein hohes Potential, die Multiplikation in einer linearen Form anschaulich darzustellen. Dies begründet sich u.a. in der Tatsache, dass der Zahlenstrahl bei vielen Schülerinnen und Schülern im schulischen Kontext bereits im Zusammenhang mit anderen Grundrechenarten thematisiert wurde.
Weiterhin lassen sich das Produkt sowie beide Faktoren am Zahlenstrahl genau ablesen, was dazu beitragen kann, mentale Bilder der Multiplikation aufzubauen. Wie die Schülerlösungen zeigen, hat sich bei vielen ein Operationsverständnis ausgebildet, allerdings ist die Darstellung am Zahlenstrahl schwierig, wenn die Muster und Strukturen noch nicht vollständig internalisiert wurden.
Dies bekräftigt die Aussage, dass die Muster und Strukturen von Anschauungsmitteln immer auch entdeckt und erlernt werden müssen (Krauthausen & Scherer 2007, S. 245).
Rechengeschichten zur Multiplikation
In diesem Kapitel werden Rechengeschichten von Kindern zur Multiplikation vorgestellt, die zum einen auf Basis einer vorgegebenen Multiplikation und zum anderen auf Grundlage eines Bildes entstanden sind.
Zunächst werden die Ergebnisse zur Rechengeschichte vorgestellt, in der die Multiplikation 6 · 5 beschrieben werden sollte, wobei den Kindern eine exemplarische Geschichte vorgegeben war. Dies ermöglichte den Schülerinnen und Schülern sich zu erinnern, was unter einer Rechengeschichte zu verstehen ist. Weiterhin wurde den Kindern die Möglichkeit geboten, eine eigene Geschichte zum Bild aus Kapitel 2.1 zu erfinden.
Eine Rechengeschichte zur Aufgabe 6 · 5
Eigenaktivität
- Erstellen Sie zunächst eine eigene Rechengeschichte zur Aufgabe 6 · 5.
- Versuchen Sie daraufhin, die Rechengeschichte sowie die jeweiligen Fragen, Rechnungen und Antworten der Kinder nachzuvollziehen. Wo entdecken Sie Schwierigkeiten beim Operationsverständnis?
Lena hat 6 Boxen. In jeder Box sind 5 Kugeln drin.

Lena hat 5 Murmeln und Julia hat 6 Lollis.

Friedrich hat 30 Spiele geladen.

Dieter hat 6 · 5 Tore insgesamt gemacht.

Hier finden Sie Interpretationsvorschläge zu den einzelnen Rechengeschichten der Kinder hinsichtlich der Fragestellungen.
Eine Rechengeschichte zur zeitlich-sukzessiven Vorstellung
Eigenaktivität
- Entwerfen Sie eine Rechengeschichte zur untenstehenden Abbildung.
- Versuchen Sie, daraufhin die Rechengeschichte sowie die jeweiligen Fragen, Rechnungen und Antworten der Kinder nachzuvollziehen. Wo entdecken Sie Schwierigkeiten beim Operationsverständnis?

Frau Müller will an ihre Leine Ballons hängen. Sie kauft 4 Bündel an der je drei Ballons befestigt sind.
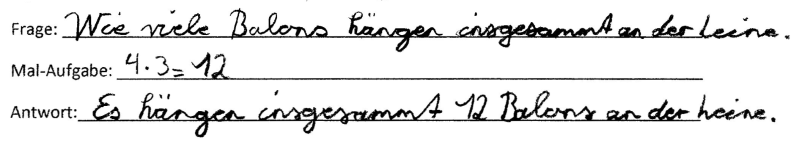
Lisa hängt Luftballons auf.

Das Mädchen Trulla hängt 6 mal 3 Ballons auf.

Finja hängt bunte Luftballons auf. Erst 3 dann wieder 3 dann wieder 3 dann wieder 3.

Lisa macht eine Party. Sie hängt Ballons auf. Und es sind immer drei gleiche Ballons.

Leonie macht eine Party und hat 4 · 3 Ballons aufgehängt.

Anna hängt die Luftballons auf die Leine. Sie hängt zuerst 3 auf und dann noch mal 3 und dann das noch mal zweimal.

Jana hat 3 Kisten. In jede Kiste passen 10 Fotos.
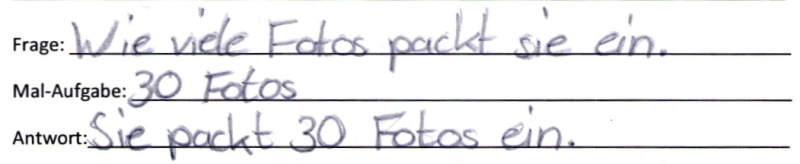
Mia hängt jeden Tag 3 Ballons auf, manchmal ist sie sehr erschöpft.

Hier finden Sie Interpretationsvorschläge zu den einzelnen Rechengeschichten der Kinder hinsichtlich der Fragestellungen.
Zusammenhang zwischen Multiplikation und Division
Eigenaktivität
Nehmen Sie sich kurz Zeit und denken Sie darüber nach, welche Multiplikations- und Divisionsaufgaben Sie im folgenden Punktefeld sehen.
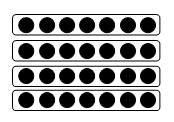
Hier finden Sie Interpretationsvorschläge.
Testen Sie Ihr Wissen zu dem Thema in unserem Kira-Check.
Verwandte Themen
Multiplikation und Division: Lernstände und Entwicklungen
Bildliche Darstellung
PIKAS: Lernstände wahrnehmen
primakom: Gestütztes Üben am Beispiel des 1x1
primakom: Materialeinsatz
Verwendetes Material
Die verwendete Standortbestimmung wurde in Anlehnung an Akinwunmi, Deutscher & Mosandl (2014) erstellt. Auszüge der Originalmaterialien sind unter folgendem Link unter den Materialien zum Förderbaustein N4 – Multiplikation und Division verstehen zu finden: Mathe sicher können: Material – Diagnose- und Fördermaterial Sek 1.
Literatur
Diese Seite wurde erstellt von Beatrice Dürdodt für das Projekt Kira.