Die Division stellt eine der vier Grundrechenarten der Mathematik dar und wird im schulischen Kontext meistens nach der Behandlung von Addition, Subtraktion und Multiplikation thematisiert.
Hier sollen Beispiele für die Bearbeitung von unterschiedlichen Aufgabenformaten dieser Grundrechenart präsentiert werden. Die beschriebenen Aufgaben wurden von Kindern der zweiten und dritten Klasse bearbeitet und sind in Anlehnung an eine Standortbestimmung der Division von Akinwunmi, Deutscher & Mosandl (2014) konzipiert.
Alle Kinder hatten im schulischen Kontext bereits Kontakt zu Divisionsaufgaben, sodass es sich hier um eine Standortbestimmung der Lösungsstrategien zu dieser Grundrechenart handelt.
Auf dieser Seite soll die Vielfältigkeit möglicher Herangehensweisen an die Division präsentiert werden und den Leserinnen und Lesern die Möglichkeit geboten werden, das Operationsverständnis der Kinder zu analysieren.
Welche Rechengeschichte passt zu diesen Bildern?
Eigenaktivität
Nehmen Sie sich kurz Zeit und schauen Sie sich die Zeichnung von den Kindern an, die auf Basis einer Rechengeschichte entstanden sind. Wie glauben Sie könnte die Rechengeschichte gelautet haben?
Hier finden Sie die zugrunde liegende Rechengeschichte.
Hier finden Sie eine mögliche Interpretation der Terme und Zeichnungen der Kinder.
Grundvorstellungen der Division
Aufteilen
Gesamtmenge: gegeben
Anzahl der Teilmengen: gesucht
Elementzahl der Teilmengen: gegeben
Verteilen
Gesamtmenge: gegeben
Anzahl der Teilmengen: gegeben
Elementzahl der Teilmengen: gesucht
Eigenaktivität
Versuchen Sie, die zwei folgenden Aufgabenstellungen den beiden Grundvorstellungen der Division zuzuordnen. Warum haben Sie sich für die entsprechende Grundvorstellung entschieden?
- Drei Kinder teilen sich 15 Weintrauben. Jedes Kind bekommt gleich viele. Wie viele Weintrauben bekommt jedes Kind?
- Es gibt 15 Weintrauben und ein paar Kinder. Jedes Kind soll fünf Weintrauben bekommen. Wie viele Kinder können Weintrauben bekommen, damit keine übrig bleibt?
Hier finden Sie eine mögliche Erklärung.
Vorstellung Divisionsaufgaben am Zahlenstrahl
Eigenaktivität
- Lösen Sie zunächst Aufgaben am Zahlenstrahl.
- Versuchen Sie daraufhin, die Lösungen der Kinder nachzuvollziehen. Können Sie dabei Chancen und Schwierigkeiten feststellen, die mit dem Zahlenstrahl als Anschauungsmittel verbunden sind?
1) Schreiben Sie zu dem Zahlenstrahl-Bild eine passende Division auf.
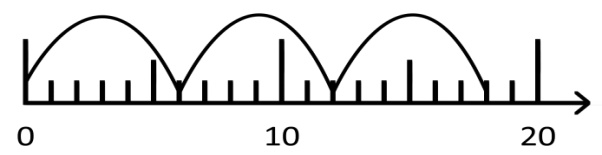
2) Zeichnen Sie zu der Division 15 : 5 ein passendes Bild in den Zahlenstrahl:
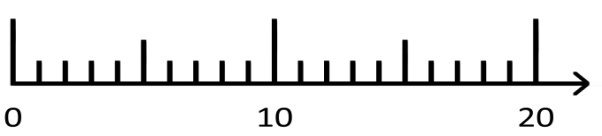
Hier finden Sie Interpretationsvorschläge zu den einzelnen Lösungsvorschlägen der Kinder hinsichtlich der Fragestellungen.
Der Zahlenstrahl bietet eine Möglichkeit, Divisionsaufgaben an einer linearen Darstellungsform zu erarbeiten. Weiterhin kann die Darstellung auf dem Zahlenstrahl die Kinder unterstützen, mentale Bilder der Operationen aufzubauen.
In den meisten Fällen haben die Kinder im schulischen Kontext bereits Kontakt zum Zahlenstrahl gehabt, wenn Additions- und Subtraktionsaufgaben gelöst wurden. Allerdings werden die Operationen bei einer Division anders dargestellt als bspw. bei der Multiplikation.
Welche Bedeutung Dividend, Divisor und Quotient haben, sollten die Kinder durchdrungen haben. Ebenfalls erscheint es wichtig, mit den Kindern die Muster und Strukturen des Anschauungsmittels zu entdecken, um die Operationen an diesem Anschauungsmittel darstellen zu können.
Rechengeschichten zur Division
In der von den Kindern bearbeiteten Standortbestimmung zur Division bekamen sie die Möglichkeit, eine eigene Rechengeschichte zu entwickeln. Hierbei wurde ihnen zunächst eine exemplarische Rechengeschichte präsentiert, anschließend konnten die Kinder ihre eigene Geschichte zur Aufgabe 36:4 verschriftlichen.
Eigenaktivität
- Erstellen Sie zunächst eine eigene Rechengeschichte zur Aufgabe 36:4.
- Versuchen Sie, die Rechengeschichte und die jeweiligen Fragen, Rechnungen und Antworten der Kinder nachzuvollziehen. Wo entdecken Sie Schwierigkeiten beim Operationsverständnis?

Hier finden Sie Interpretationsvorschläge zu den einzelnen Rechengeschichten der Kinder hinsichtlich der Fragestellungen.
Das geht doch nicht - Division mit Rest
Die Division mit Rest bietet den Kindern die Möglichkeit, die scheinbar bestehende Konvention, dass immer eine natürliche Zahl als Quotient notiert werden kann, zu überwinden. Im Hinblick auf die Vorbereitung und das Verständnis von Dezimalzahlen und Brüchen, ist das Thematisieren der Division mit Rest relevant und hilft bereits früh, Fehlvorstellungen vorzubeugen.
Wichtig scheint es weiterhin zu sein, eine einheitliche Darstellungsform zu verwenden, da so richtig durchgeführte Rechnungen, wie die von Lukas, hinsichtlich mathematischer Konventionen nicht korrekt notiert sind. Dies gilt ebenfalls für Sina und Klara, die in ihrer Rechnung und Argumentation von der Grundidee ausgehen, dass 35 ohne Rest geteilt werden kann und dies korrekt notieren. Für die Notation des Restes finden sie kreative Lösungsvorschläge, die auf ein Verständnis der Division mit Rest hinweisen.
Testen Sie Ihr Wissen zu dem Thema in unserem Kira-Check.
Verwandte Themen
- Aufteilen und Verteilen
- Bildliche Darstellung
- Division mit Rest
Hier finden Sie eine inhaltliche Auseinandersetzung und Vertiefung zur Thematik der bildlichen Darstellung.
Hier finden Sie eine inhaltliche Auseinandersetzung und Vertiefung zur Thematik der Division mit Rest.
Verwendetes Material
Die verwendete Standortbestimmung wurde in Anlehnung an Akinwunmi, Deutscher & Mosandl (2014) erstellt. Auszüge der Originalmaterialien sind unter folgendem Link unter den Materialien zum Förderbaustein N4 – Multiplikation und Division verstehen zu finden: Mathe sicher können: Material – Diagnose- und Fördermaterial Sek 1.
Literatur
Diese Seite wurde erstellt von Beatrice Dürdodt für das Projekt Kira.